1. 引言

在现代机器学习应用中，数据的维度通常非常高，这意味着我们需要处理成千上万的特征。然而，高维数据并不总是有益的，冗余的或不相关的特征可能会导致模型复杂化、计算时间增加，并降低模型的泛化能力。因此，如何有效地减少数据的维度成为了一个重要的研究方向。主成分分析（PCA）作为一种常用的降维技术，广泛应用于数据预处理、特征提取、数据压缩等场景中。本篇博客将详细介绍PCA的基本原理、算法步骤及其在机器学习中的应用。

2. 什么是降维？

降维是指将高维数据映射到一个较低维度的空间，同时尽量保留原始数据的重要信息。在机器学习中，降维的主要目的是减少数据的特征数目，简化模型的复杂性，提高模型的计算效率，同时帮助我们更好地理解数据的结构。

高维数据的挑战

• 维度诅咒：随着数据维度的增加，数据空间会变得极其稀疏，导致机器学习算法难以找到有效的模式。
• 计算复杂度：高维数据通常需要更长的计算时间和更大的内存空间。
• 可视化困难：人类直观地理解三维及以下的数据，对于高于三维的数据，直观理解变得几乎不可能。

降维的应用场景

• 数据可视化：通过降维可以将高维数据映射到二维或三维空间，从而可以直观地进行数据可视化。
• 特征提取：通过降维可以去除冗余信息，提取数据中最重要的特征。
• 噪声过滤：通过降维可以去除数据中的噪声，保留数据的主要信息。

3. PCA的基本原理

PCA，全称Principal Component Analysis，是一种线性降维技术。它通过线性变换将数据投影到新的坐标系中，使得新坐标系的各个维度（即主成分）之间互不相关，并且尽可能地保留原始数据的方差。

特征值和特征向量

• 特征值表示了数据在某个方向上的方差大小。
• 特征向量表示了这个方向的具体位置。

数据协方差矩阵

• 协方差矩阵是用来衡量两个变量之间线性相关性的一个矩阵。通过计算数据的协方差矩阵，我们可以了解不同特征之间的关系。

PCA的核心思想

• 通过计算数据的协方差矩阵，找出数据的主成分，即数据方差最大的方向。主成分的个数通常比原始特征的个数少，这样可以有效地降维。

4. PCA算法步骤

1. 数据标准化

   • 在PCA之前，我们通常会对数据进行标准化处理，使得每个特征的均值为0，方差为1。这一步是为了防止某些特征由于尺度较大而对PCA的结果产生不合理的影响。

2. 计算协方差矩阵

   • 标准化后的数据用于计算协方差矩阵，协方差矩阵反映了数据集中不同特征之间的关系。

3. 计算特征值和特征向量

   • 通过求解协方差矩阵的特征值和特征向量，我们可以找出数据的主成分。

4. 选择主要成分

   • 根据特征值的大小排序，选择前k个最大的特征值对应的特征向量，作为新的特征空间的基向量。

5. 投影数据到新的特征空间

   • 使用选定的特征向量将原始数据投影到新的低维特征空间，从而完成降维。

5. PCA降维的优缺点

优点：

• 降低维度：PCA能够减少特征的数量，从而简化模型结构，减少计算成本。
• 保留重要信息：PCA通过最大化方差来保留数据的主要信息。
• 减少噪声：PCA可以通过去除低方差的成分来减少数据中的噪声。

缺点：

• 信息损失：PCA是线性降维方法，在降低维度的过程中可能会丢失一些信息，尤其是非线性数据。
• 解释性减弱：降维后，新的主成分通常很难与原始特征直接对应，这可能会减弱结果的可解释性。

6. PCA的应用场景

数据可视化

• PCA可以将高维数据压缩到二维或三维空间，从而使数据的可视化变得可行。例如，PCA常用于处理MNIST手写数字数据集，将784维的图像数据压缩到二维空间，从而可视化不同类别的分布。

图像压缩

• 在图像处理中，PCA可以用于图像压缩。通过PCA将图像数据降维，可以在保留主要信息的同时显著减少存储空间。例如，将一张高分辨率图片的像素矩阵使用PCA降维，可以实现图像的压缩传输。

噪声过滤

• PCA还可以用于去除数据中的噪声。通过选择主成分并舍弃低方差的次要成分，可以有效过滤掉数据中的噪声，从而提高数据的质量。

在机器学习模型中的使用

• 在训练机器学习模型时，PCA可以作为数据预处理的一步，减少特征维度，从而提高模型的训练速度和性能。例如，在分类任务中，使用PCA可以减少数据的冗余性，提高模型的泛化能力。

7. PCA的实现

在实际操作中，PCA可以通过Python的scikit-learn库轻松实现。以下是PCA的一个简单实现示例：

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt

# 生成一些示例数据
X = np.array([[2.5, 2.4],
              [0.5, 0.7],
              [2.2, 2.9],
              [1.9, 2.2],
              [3.1, 3.0],
              [2.3, 2.7],
              [2.0, 1.6],
              [1.0, 1.1],
              [1.5, 1.6],
              [1.1, 0.9]])

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 初始化PCA，选择保留两个主成分
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 可视化降维后的数据
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c='blue', marker='o', edgecolor='k')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA on Sample Data')
plt.grid(True)
plt.show()

print("降维后的数据：\n", X_pca)
print("解释方差比率：\n", pca.explained_variance_ratio_)

代码说明：
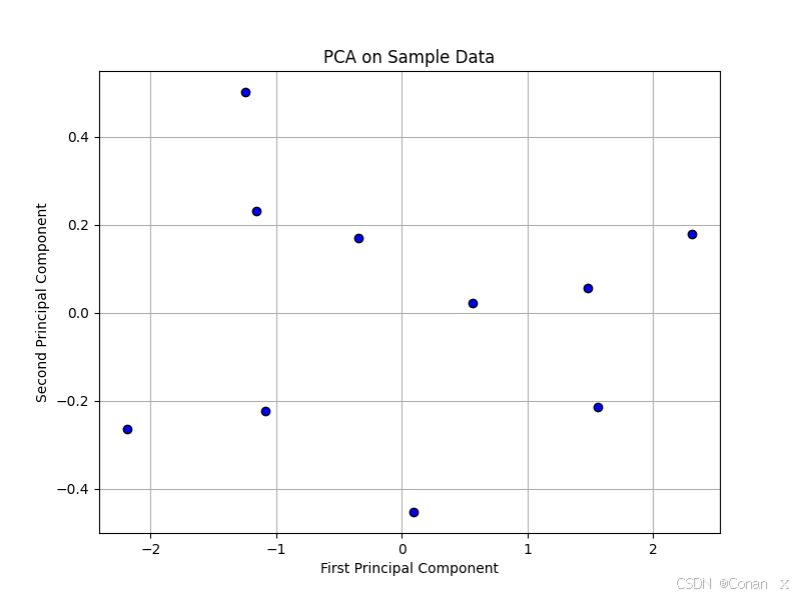
我们首先生成了一些二维示例数据，并对其进行标准化处理。接着，我们使用PCA对数据进行了降维，并选择了两个主成分。通过matplotlib库，我们将降维后的数据进行了可视化展示。图中显示了降维到二维空间的结果，其中横轴和纵轴分别代表第一个和第二个主成分。在图中，我们可以直观地看到数据在降维后的新特征空间中的分布情况。

如何选择合适的主成分数量

• 在实际应用中，选择多少个主成分往往是一个权衡的过程。通常，我们会根据累积解释方差比率（Cumulative Explained Variance Ratio）来选择主成分的数量。例如，如果前两个主成分已经解释了95%以上的方差，我们可能会选择这两个主成分作为最终的降维结果。

8. PCA与其他降维技术的比较

PCA vs. LDA（线性判别分析）

• PCA是一种无监督的降维方法，主要关注的是最大化方差，而LDA是一种有监督的降维方法，旨在最大化类间方差与类内方差之比。
• LDA通常在分类任务中效果更佳，因为它利用了标签信息。
  PCA vs. t-SNE（t分布邻域嵌入）
• t-SNE是一种非线性降维方法，通常用于高维数据的可视化，尤其是在降维到2D或3D时，t-SNE能更好地捕捉局部结构。
• PCA计算速度更快，但可能无法很好地捕捉复杂的非线性关系。

PCA vs. UMAP（统一流形近似和投影）

• UMAP也是一种非线性降维方法，通常比t-SNE更快，并且能够更好地保留全局结构。
• PCA在处理线性关系数据时可能更优，但在需要保持数据的局部和全局结构时，UMAP更具优势。

from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.manifold import TSNE
import umap
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np

# 加载示例数据集（Iris数据集）
data = load_iris()
X = data.data
y = data.target

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 1. PCA降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 2. LDA降维
lda = LDA(n_components=2)
X_lda = lda.fit_transform(X_scaled, y)

# 3. t-SNE降维
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)

# 4. UMAP降维
umap_model = umap.UMAP(n_components=2, random_state=42)
X_umap = umap_model.fit_transform(X_scaled)

# 绘制比较图
plt.figure(figsize=(16, 10))

plt.subplot(2, 2, 1)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', edgecolor='k')
plt.title('PCA')

plt.subplot(2, 2, 2)
plt.scatter(X_lda[:, 0], X_lda[:, 1], c=y, cmap='viridis', edgecolor='k')
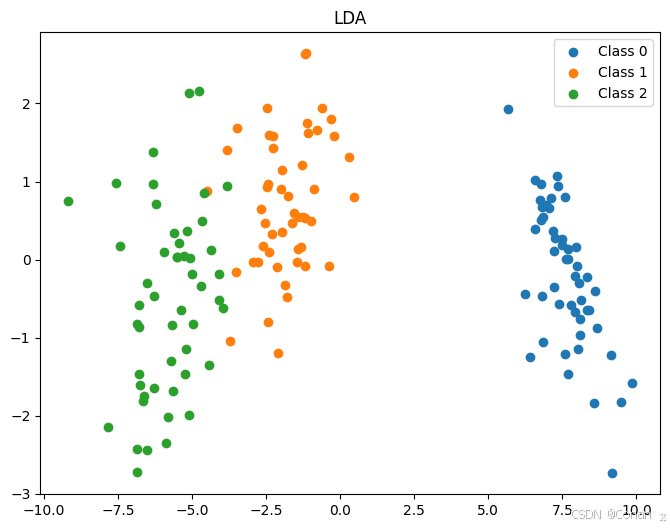
plt.title('LDA')

plt.subplot(2, 2, 3)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='viridis', edgecolor='k')
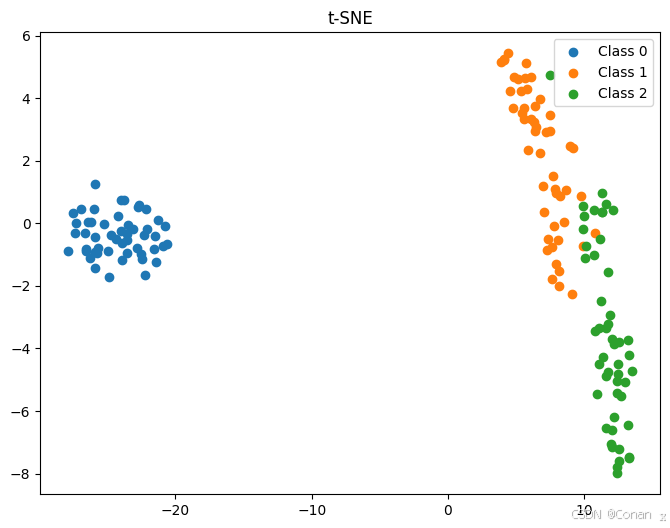
plt.title('t-SNE')

plt.subplot(2, 2, 4)
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=y, cmap='viridis', edgecolor='k')
plt.title('UMAP')

plt.suptitle('Comparison of PCA, LDA, t-SNE, and UMAP')
plt.show()

代码说明：

我们使用了Iris数据集，该数据集包含150个样本，每个样本有4个特征，分为3类。

数据标准化后，我们分别使用PCA、LDA、t-SNE和UMAP进行降维，将数据降至二维。

使用matplotlib库将每种降维方法的结果进行了可视化展示。

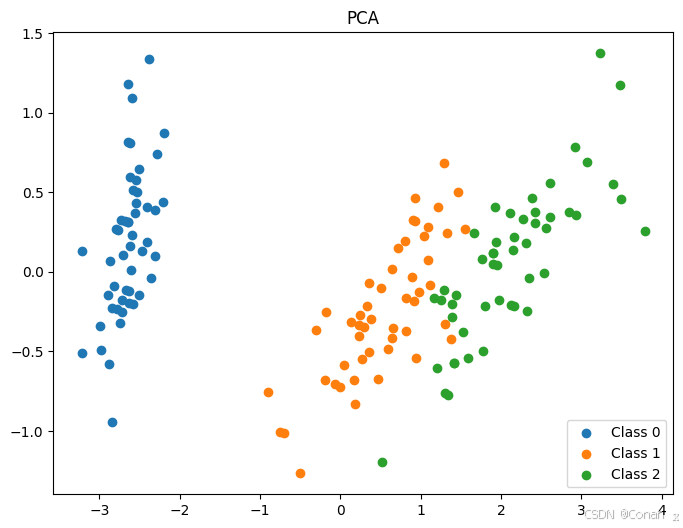
可视化结果解读：

PCA：PCA是无监督的降维方法，主要关注数据的方差，因此降维后的数据可能会在某些类别上存在重叠。

LDA：LDA是一种有监督的降维方法，它利用了类别标签来最大化类间方差，因此通常在分类任务中表现较好。可以看到LDA能更好地分离不同类别的数据。

t-SNE：t-SNE是一种非线性降维方法，特别适用于高维数据的可视化。它能够很好地保持局部结构，但在全局结构上可能不如PCA。

UMAP：UMAP是一种非线性降维方法，通常比t-SNE更快，并且能够更好地保留全局和局部结构的平衡。

9. PCA的常见误区

**误区1：PCA总

能提高模型的性能**

• 虽然PCA能够减少数据维度，但它并不总能提高模型的性能。对于一些复杂的非线性数据集，PCA可能会丢失重要信息，反而降低模型效果。

误区2：PCA适用于所有数据集

• PCA假设数据的主要信息通过最大方差来表示，但对于一些特殊数据集，这一假设可能不成立。例如，PCA可能不适用于分类边界复杂的数据集。

误区3：主成分数量越少越好

• 主成分数量的选择需要平衡信息保留和降维效果。如果选择的主成分数量过少，可能会导致信息的丢失，影响模型性能。

10. 总结与展望

PCA作为一种经典的降维方法，在机器学习的多个领域中都有广泛的应用。通过减少数据维度，PCA能够帮助我们更好地理解数据结构，提升模型效率。然而，PCA也有其局限性，如可能丢失非线性信息。在未来，随着数据复杂性的增加和计算能力的提升，我们可能会看到PCA与其他降维技术（如深度学习中的自动编码器）结合，形成更强大的数据处理工具。

11. 附录

参考文献和学习资源推荐

• 《Pattern Recognition and Machine Learning》 by Christopher Bishop
• Scikit-learn PCA Documentation
• PCA Overview on Towards Data Science

通过这些资源，读者可以深入学习PCA的理论基础和实战应用，进一步提升对PCA的理解和使用能力。