Scikit-Learn逻辑回归一
1、逻辑回归概述
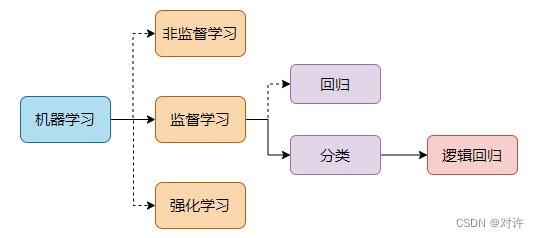
逻辑回归(Logistic Regression)主要解决二分类问题,用来表示某个事件发生的可能性。逻辑回归在机器学习知识结构中的位置如下:
1.1、逻辑回归
逻辑回归的思想最早可以追溯到19世纪,由英国统计学家Francis Galton在研究豌豆遗传问题时首次提出。然而,真正将逻辑回归应用于机器学习的是加拿大统计学家Hugh Everett,他在1970年代提出了广义线性模型(GLM),其中包括逻辑回归
逻辑回归这个算法的名称有一定的误导性。虽然它的名称中有“回归”,但它在机器学习中不是回归算法,而是分类算法。因为采用了与回归类似的思想来解决分类问题,所以它才会被称为逻辑回归
在逻辑回归中,我们不是直接预测输出值,而是预测输出值属于某一特定类别的概率。例如,一封邮件是垃圾邮件的概率(是与不是),广告被点击的概率(点与不点)等
逻辑回归通过Sigmoid函数将样本的特征与样本发生的概率联系起来,在拟合样本数据发生概率的时候,其实是在解决一个回归问题,当概率计算出来后,再根据概率进行分类处理。逻辑回归是在解决样本与样本发生的概率之间的回归问题
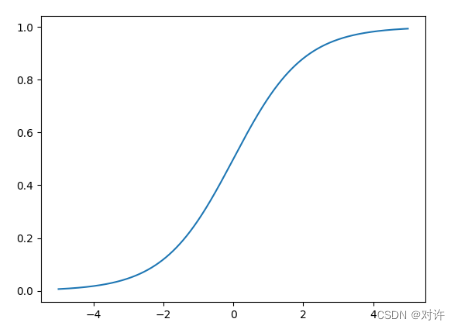
逻辑回归的函数表达式(Logistic函数或Sigmoid函数)为
g ( z ) = 1 1 + e − z \rm g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
Sigmoid函数有时也用 σ ( z ) \sigma(z) σ(z)表示,其对应的图像为
import numpy as np
import matplotlib.pyplot as plt
z = np.arange(-5, 5, 0.01)
y = 1/(1+np.exp(-z))
plt.plot(z, y)
plt.show()
逻辑回归基于概率来进行分类。对于给定输入特征X,逻辑回归模型会计算输出标签y=1(正类)的条件概率:
P ( y = 1 ∣ X ) = 1 1 + e − ( θ T X + b ) P(y=1|X)=\frac{1}{1+e^{-(\theta^T X+b)}} P(y=1∣X)=1+e−(θTX+b)1
其中, ω \omega ω是特征权重,b是偏置项
逻辑回归将线性回归的结果 y y y= θ T X \theta^T X θTX+ b b b带入到Sigmoid函数的自变量,并将其映射到0和1之间,使其可以解释为概率
逻辑回归与线性回归的关键区别在于,后者训练出来的模型的预测值域为( − ∞ -∞ −∞,+ ∞ ∞ ∞),换句话说,也就是对值域没有限制;而对于表示概率的值而言,其值域都是在(0,1)之间
更多关于逻辑回归的介绍见文章:传送门
1.2、逻辑回归的优缺点
优点:
- 模型简单,分类计算量小,存储资源低,训练和预测速度快
- 预测结果是观测样本的概率,易于理解,增加了解释性
- 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题
缺点:
- 只能处理二分类问题,且逻辑回归假设数据是线性可分的,对于非线性特征,需要进行转换
- 容易欠拟合,一般准确度不太高
1.3、逻辑回归与线性回归
逻辑回归与线性回归的区别详见文章:传送门
2、逻辑回归的原理
2.1、逻辑回归的概念与原理
逻辑回归的概念与原理推导详见文章:传送门
2.2、逻辑回归的损失函数
在逻辑回归(详见:传送门)一文中,我们已经给出并推导了逻辑回归的损失函数
J ( θ ) = − 1 m ∑ i = 1 m [ y i ln y ^ i + ( 1 − y i ) ln ( 1 − y ^ i ) ] J(\theta)=-\frac{1}{m}\sum_{i=1}^m[y_i\ln \hat y_i+(1-y_i)\ln(1-\hat y_i)] J(θ)=−m1i=1∑m[yilny^i+(1−yi)ln(1−y^i)]
其中 y y y为真实标签值, y ^ \hat y y^= 1 1 + e − θ T X \frac{1}{1+e^{-\theta^T X}} 1+e−θTX1为预测值。它是多个样本的平均损失。对于单个样本,其损失函数拆分后表示为
c o s t = { − ln ( p ) y = 1 − ln ( 1 − p ) y = 0 cost=\begin{cases} -\ln(p) \, \, & y=1 \\ -\ln(1-p) \, \, & y=0 \end{cases} cos