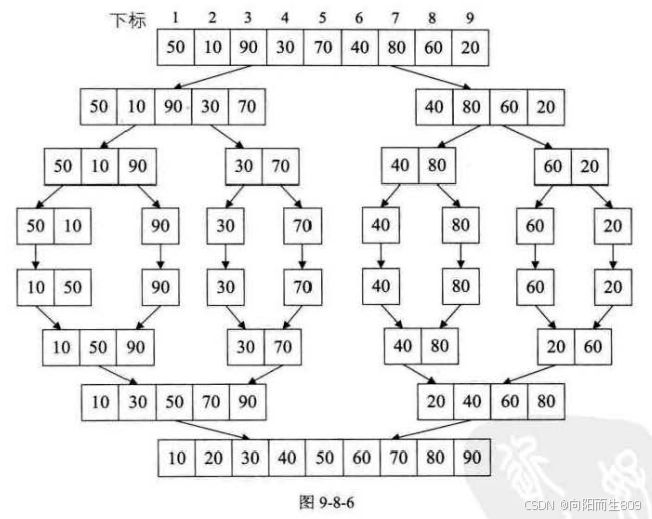
一、归并排序的概念

归并排序（Merge Sort）是一种分治策略的排序算法，它通过将数组分成两半，递归地对每一半进行排序，然后再将排序好的两半合并成一个有序数组。归并排序的时间复杂度在最好、平均和最坏情况下均为O(n log n)，并且是稳定的排序算法。

二、归并排序的原理

1. 分解：将数组分成两半，递归地对每一半进行排序。

2. 合并：将排序好的两个子数组合并成一个有序数组。

三、代码分析：

逻辑步骤：

1. 分解：如果数组的长度大于1，则将数组分成两个相等长度的子数组。

2. 递归排序：递归地对每个子数组进行归并排序。

3. 合并：将两个已排序的子数组合并成一个有序数组。

#include <stdio.h>
void print(int *arr, int size)
{
    for (int i = 0; i < size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
/*merge将数组分成两组，并对两组数组进行合并（按大小顺序）*/
void merge(int *arr, int left, int mid, int right)
{
    int n1 = mid - left + 1;
    int n2 = right - mid;
    /*创建临时数组*/
    int L[n1], R[n2];

    /*复制数据到临时数组*/
    for (int i = 0; i < n1; i++)
    {
        L[i] = arr[i + left];
    }
    for (int j = 0; j < n2; j++)
    {
        R[j] = arr[j + mid + 1];
    }

    /*合并临时数组回原数组*/
    int i = 0;// 初始索引 of 第一个子数组
    int j = 0;// 初始索引 of 第二个子数组
    int k = left;// 初始索引 of 合并后的子数组
    while(i < n1 && j < n2)
    {
        if(L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else{
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while(i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }

    while(j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }

}

/*mergeSort：该函数用于递归地对数组进行排序。*/
void mergeSort(int *arr, int left, int right)
{
    if (left < right)
    {
        int mid = left + (right - left) / 2;
        /*递归地排序两个数组*/
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        /*合并两个数组*/
        merge(arr, left, mid, right);
    }
}

int main()
{
    int arr[] = {5, 4, 6, 2, 1, 3, 0};
    int size = sizeof(arr) / sizeof(int);
    printf("归并排序前的数组元素如下：");
    print(arr,size);
    printf("归并排序后的数组元素如下：");
    mergeSort(arr, 0, size - 1);
    print(arr,size);
    return 0;
}

运行结果：

四、复杂度分析

1、时间复杂度

最好情况、平均情况和最坏情况：时间复杂度均为O(n log n)。

2、空间复杂度

空间复杂度：O(n)

因为归并排序需要额外的空间来存储临时数组。归并排序是一种高效的排序算法，尤其适用于大数据集。它不仅稳定，而且在各种情况下都能保持较好的性能。