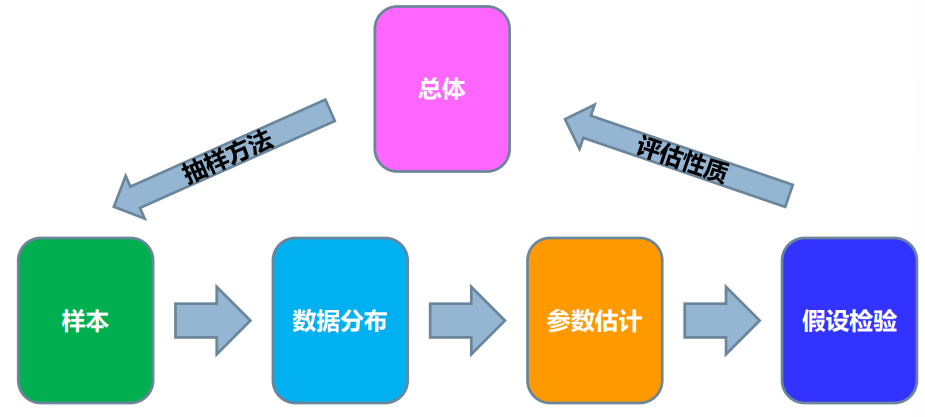
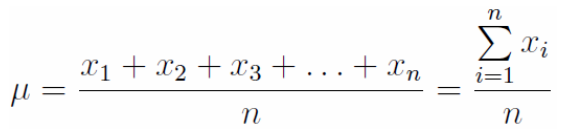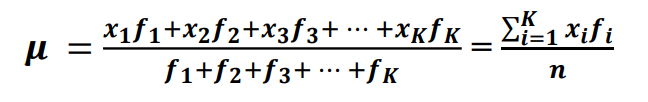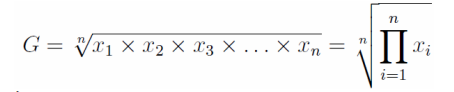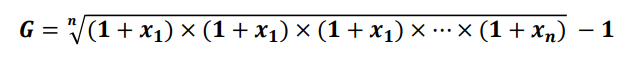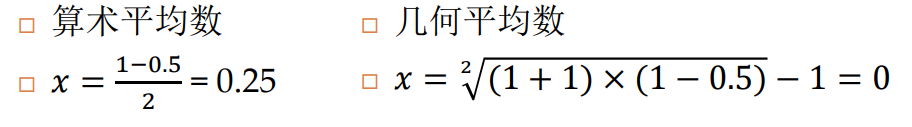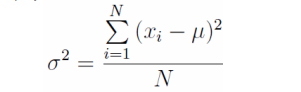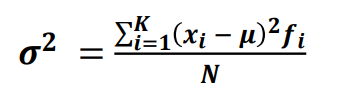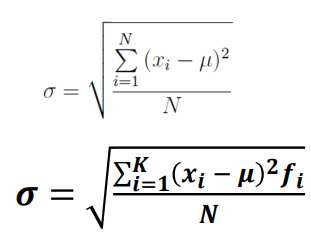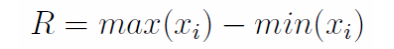【数据统计】— 数据分布
数据分布基本指标
- 在对大数据进行研究时,首先希望知道所获得的数据的基本分布特征
- 数据分布的特征可以从三个方面进行测度和描述:
- 描述数据分布的集中趋势:反映数据向其中心靠拢或聚集程度
- 描述数据分布的离散程度:反映数据远离中心的趋势或程度
- 描述数据分布的形状变化:反应数据分布的形状特征
集中趋势
- 集中趋势反映了一组数据的中心点位置所在及该组数据向中心
靠拢或聚集的程度。 - 四种最常用的反映数据集中趋势的指标:
- 平均数
- 中位数
- 分位数
- 众数
平均数
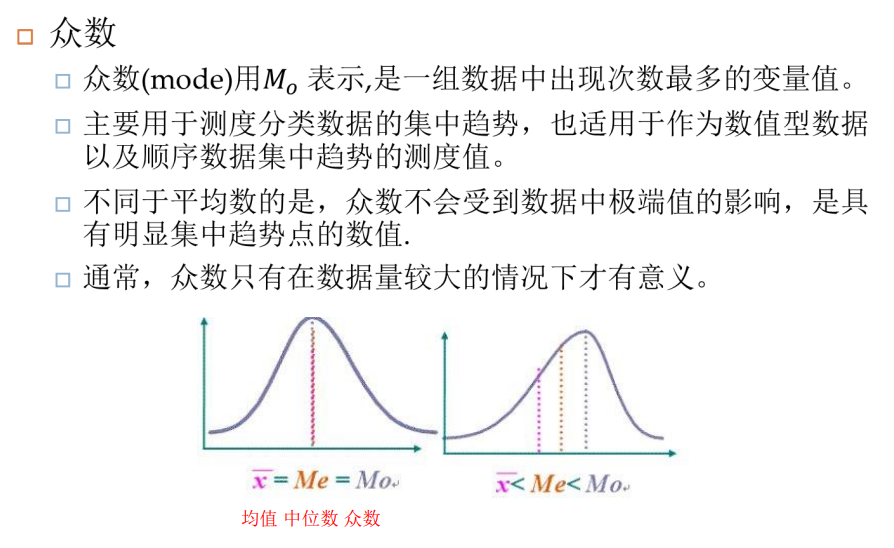
- 平均数也称均值(mean),它是一组数据相加后除以数据的个数得到的结果,是集中趋势最主要的指标。
- 主要适用于数值型数据,而不适用于分类数据和顺序数据。
简单平均数(simple mean): 算术平均数
-
根据未经分组数据计算得到的平均数
-
若有一组数据:𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑛, 则简单平均数为:
-
特点:易受极端值的影响
加权平均数(weighted mean)
- 根据分组数据计算的平均数
- 若有一组n个数据分为K组,各组的值表示为:𝑥1, 𝑥2, 𝑥3, ⋯,𝑥K,
- 各组变量出现的频数表示为:𝑓1, 𝑓2, 𝑓3, ⋯,𝑓𝑘,
- 则该数据的加权平均数为:
- 特点:
- 影响因素:组数值,频数
- 频数越多,该组影响最大
几何平均数(geometirc mean)
-
几何平均数是n个变量值乘积的n次方根
- 适用范围
- 平均比率:年利率、合格率等
- 适用范围
-
若一组数据𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑛,则该组数据的几何平均数为
-
若数值为增长率
-
特点
- 几何平均数受极端值的影响较算术平均数小
- 如果变量值有负值,计算出的几何平均数就会成为负数或虚数
- 几何平均数的对数是各变量值对数的算术平均数
算术平均数 vs 几何平均数
- 例:一只股票价格第一年初价格为10元,第一年增长了100%,第二年下降了50%,计算两年平均增长率?
中位数
分位数
- 中位数用1 个点将数据两等分
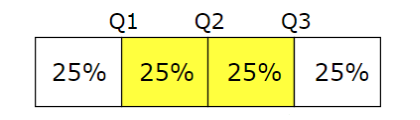
- 类似的,若用3 个点将数据四等分、9 个点将数据十等分、99 个点将数据一百等分,则对应等分点上的值为四分位数(quartile)、十分位数(decile) 和百分位数(percentile)
- 四分位数也称四分位点,它通过3 个点将数据等分成四个部分
- 中间的四分位数就是中位数
- 下四分位数:处在25% 位置上的数值,第一四分位数
- 上四分位数:处在75% 位置上的数值,第三四分位数
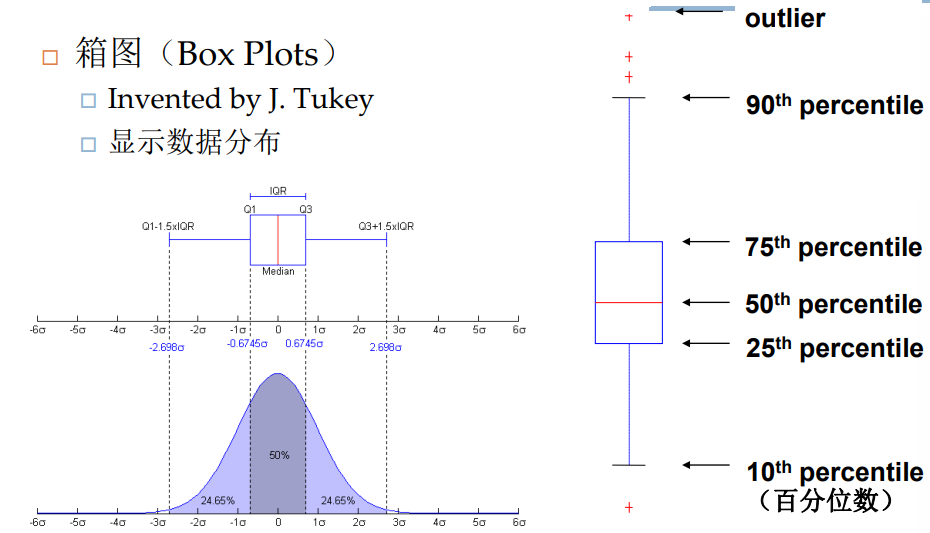
- 四分位距IQR:Q3-Q1
箱图
- 相对稳定的方式描述数据分布
- 不受异常值影响,识别了异常值
众数
离散程度
- 离散程度反映了各个数据属性值远离其中心值的程度,是数据分布的另一个重要特征。
- 数据的离散程度越大,则集中趋势的测度值对该组数据的代表性就越差,反之亦然。
- 四种最常用的反映数据离散程度的指标:
- 方差和标准差
- 极差和四分位差
- 异众比率
- 变异系数
方差和标准差
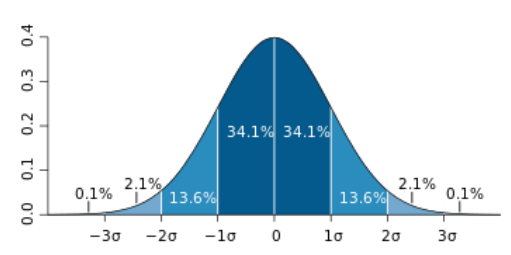
- 在数值型数据中, 刻画数据围绕其中心位置附近分布的数字特征时,最重要且最常用的是方差(variance) 和标准差(standard deviation)
- 衡量平均数对数据的代表性
- 方差是各个变量与均值之差平方的平均数
- 标准差为方差的平方根,两个指标均能较好地反映出数值型数据的离散程度
方差
-
对于未分组数据𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑁,数据的算术平均数为𝜇。数据的总体方差为
-
对于已分为K组的N个数据,各组的值表示为:𝑥1, 𝑥2, 𝑥3,⋯,𝑥K, 各组变量出现的频数表示为:𝑓1, 𝑓2, 𝑓3, ⋯,𝑓𝑘, 数据的加权平均数为𝜇,则数据的总体方差为
标准差
- 标准差为方差的算数平方根,具有量纲(与原数据有相同单位)
- 它与变量值的计量单位相同,实际意义比方差更清楚。
- 对于未分组数据和加权的分组数据(K组)来说,其标准差的计算公式分别为:
极差和四分位差
- 在顺序数据中,当中位数为数据中心位置的指标时,可以用极差或者四分位差反映数据的离散程度
- 衡量中位数对数据的代表性
极差
- 一组数据的最大值和最小值之差为极差(range),也被称为全矩®, 描述数据离散程度的最简单的测度值
- 一组数据𝑥1, 𝑥2, 𝑥3, ⋯,𝑥𝑁,则该组数据的极差为
- 特点
- 极差是数据的振幅,振幅越大表示数据越分散
- 极差只利用了一组数据的两端信息,易受极端值影响。若大部分数据集中在一个较窄的范围,极端值的数据较少,则极差不能准确描述数据的分散程度,即不能反映中间数据的分散程度。