一.定义
二叉搜索树是一种队排序和查找都很有用的特殊二叉树。又称为二叉排序树和二叉查找树。其定义如下:
1.二叉查找树为空树
2.非空左子树所有结点的值小于根节点的值
3.非空右子树所有结点的值大于根节点的值
4.左右子树都是二叉搜索树
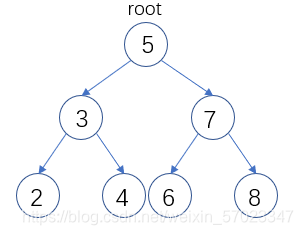
事例:如图就是一颗二叉搜索树,根节点值为5,其左子树值均小于5,右子树的值均大于5,并且在左子树,右子树中均符合这种情况。
二.基本操作
树信息:
typedef int Elementtype;
typedef struct TreeNode{
Elementtype val;
struct TreeNode *left;
struct TreeNode *right;
}Tree;
Tree *FindNode(Tree *obj, Elementtype x);//查找
int MaxData(Tree *obj);//找树的最大值
int MinData(Tree *obj);//找树的最小值
Tree *InsertNode(Tree **obj,Elementtype x);//插入,
Tree *DeletNode(Tree **obj, Elementtype x);//删除
这里的删除与插入为什么传入二级指针,而查找不需要二级指针?
因为插入与删除改变的是树的结构,要往树里插入或删除结点,而我在主函数里定义的是一个树指针变量初始化为空(如下图),改变树结构要将地址作为参数传递(传址)。而查找并没有改变树结构,所以只要传参。
如果,你是封装一个函数创建一树节点,即动态申请内存,将树信息值初始化后返回一地址,就不需要将定义的树指针的地址作为参数传入函数了。树指针变量里存的就是结点地址。
验证代码:
#include"searchtree.h"
int main(){
Tree *s = NULL;
InsertNode(&s, 5);
InsertNode(&s, 1);
InsertNode(&s, 3);
InsertNode(&s, 7);
InsertNode(&s, 6);
InsertNode(&s, 4);
InsertNode(&s, 2);
DeletNode(&s, 6);
//int max = MaxData(s);
//printf("%d\n", max);
//int min = MinData(s);
//printf("%d\n", min);
//Tree *t = FindNode(s, 8);
system("pause");
return 0;
}
1.查找
查找某一结点
在二叉搜索树中找到值为x的结点,并返回地址。
思想:由于二叉搜索树的定义与性质,过程如下:
1. 如果树为空树,返回空,查找失败
2. 如果查找值x比根结点值大,往右子树找。
3. 如果查找值x比根结点值小,往左子树找
4. 如果查找值x等于根节点值,返回地址,查找成功。
代码如下:
//这里注意是先return,再递归函数,要将最后的找到的值一直返回。
Tree *FindNode(Tree *obj, Elementtype x){//递归
if (obj == NULL){
return obj;
}
if (obj->val > x){
return FindNode(obj->left, x);
}
else if (obj->val < x){
return FindNode(obj->right, x);
}
else{
}
return obj;
}
由于递归效率一般比非递归的效率低,一般使用非递归迭代的方式实现查找。
//找某一树结点值为x的结点
//迭代方法,循环,当树不为空时,根据二叉搜索树的性质
//如果结点值比要找的值x大
//往左找,如果小往右找,退出循环时两种条件,为空和找到了
Tree *FindNode(Tree *obj, Elementtype x){//迭代
while (obj){
if (obj->val > x){
obj = obj->left;
}
else if (obj->val < x){
obj = obj->right;
}
else{
break;
}
}
return obj;//如果树为空,返回空,没找到,不为空返回地址。
}
查找树的最大值:
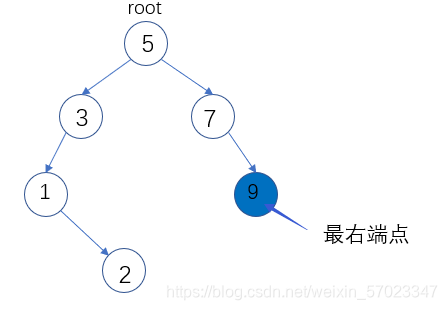
思路:最大值肯定在右边,并且时一直往右子树走,直到结点的右子树为空,当前结点的值就是树的最大值。
int MaxData(Tree *obj){//递归
if (obj == NULL){
return 0;//obj等于空,返回0
}
if(obj->right){
return MaxData(obj->right);
}
return obj->val;
}
迭代:
//根据二叉树的性质,一直往右找,最大的那个结点的右边肯定为空(退出条件)
int MaxData(Tree *obj){//迭代
if (obj == NULL){
return 0;//obj等于空,返回0
}
while (obj->right){
obj = obj->right;
}
return obj->val;
}
查找树的最小值:
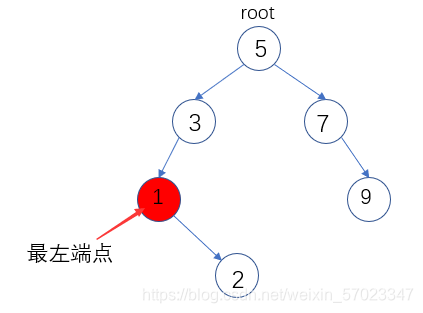
思路:最小值肯定在左子树,并且时一直往左子树走,直到结点的左子树为空,当前结点的值就是树的最小值。
递归:
int MinData(Tree *obj){//递归
if (obj == NULL){
return 0;
}
if (obj->left){
return MinData(obj->left);
}
return obj->val;
}
迭代:
//根据二叉树的性质,一直往左找,最小的那个结点的左边肯定为空(退出条件)
int MinData(Tree *obj){//迭代
if (obj == NULL){
return 0;
}
while (obj->left){
obj = obj->left;
}
return obj->val;
}
上面两个函数不仅可以实现找到树的最大值与最小值,还能实现找到左子树的最大值,右子树的最小值。
对于为什么要实现找树的最大值与最小值?在后面删除时会用到。
2.插入
根据二叉树的性质,插入的结点一定会作为叶节点插入,不会插入到两个结点中间,我实现的插入,如果结点存在的话,就不进行插入。
思路:(与查找的思路差不多,但是返回不一样,将结点返回给上一节点)
**插入的点一定是查找失败的点,并且一定是空节点**。
1. 为空直接创建新节点插入
2. 如果插入值x比根结点值大,往右子树找插入点
3. 如果插入值x比根结点值小,往左子树找插入点
4. 如果插入值x等于根节点值,说明节点已经存在,不进行插入。
5. 如果没有值与插入值x相等并且,走到节点为空,说明查找失败,即为插入点。
要插入树节点,先创造一树节点
static Tree *TreeNodecreate(Elementtype x){//建立树节点
Tree *treenode = (Tree *)malloc(sizeof(Tree));
treenode->left = NULL;
treenode->right = NULL;
treenode->val = x;
return treenode;
}
插入:
//插入的结点肯定会作为叶节点插入
//跟查找差不多,只是要找到插入位置(肯定为空结点),然后建一个结点返回。如果不是空结点说明存在这个结点。
//注意这里不是一直return,是将子节点结点的地址赋给父节点后再返回,相当于一层一层返回。
Tree *InsertNode(Tree **obj, Elementtype x){
if (*obj == NULL){
*obj = TreeNodecreate(x);
}
else{
if ((*obj)->val > x){
(*obj)->left = InsertNode(&((*obj)->left), x);//不是return,而是返回给上一节点
}
else if ((*obj)->val < x){
(*obj)->right = InsertNode(&((*obj)->right), x);
}
else{
printf("已存在\n");
}
}
return *obj;
}
3.删除
删除比其它操作复杂一点,但是思路与之前一样,只是考虑情况比较多。
思路:先找到要删除的点,再进行删除。
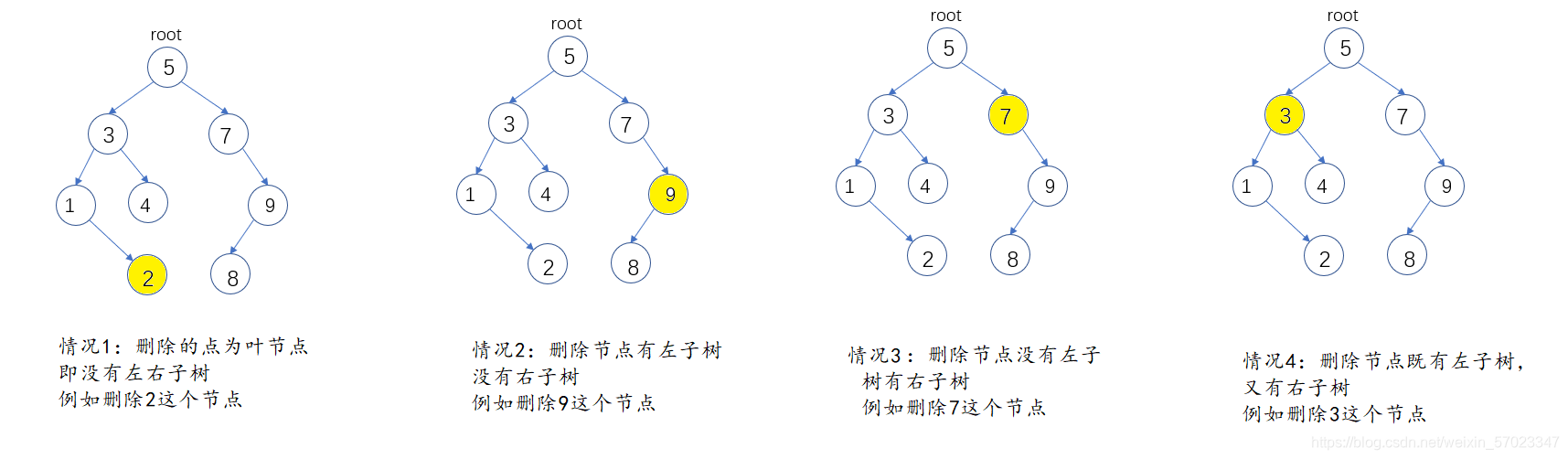
删除时要考虑四种情况:
情况1:删除节点为叶节点
这种情况最简单,直接将其置空,释放,然后返回给父节点即可。
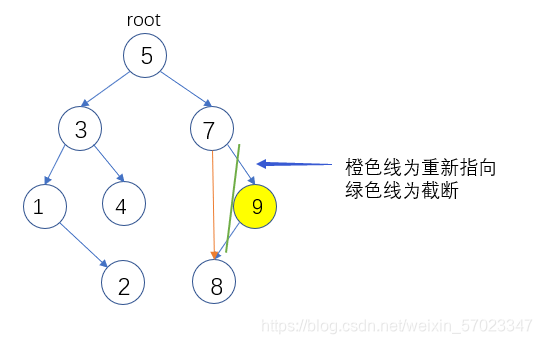
情况2:删除节点有左子树没有右子树
先保存该节点的地址(方便释放),将该节点直接等于左子树地址,也就是将该节点指向左子树。
相当于该节点存的就是左子树的地址,将原来节点地址覆盖了。然后释放。
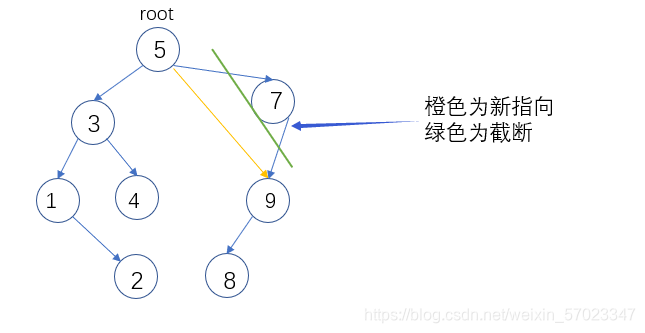
情况3:删除节点有右子树没有左子树
与情况二处理相同,只是将左子树换为右子树。
情况4:既有左子树又有右子树
可以有两种解决办法:
1.找到左子树中的最大值,将值赋给给节点,然后将左子树最大值这个节点删除(删除可以用递归实现)
2.找到左子树中的最小值,将值赋给给节点,然后将右子树最小值这个节点删除
当时这样会有个弊端:当一直删除时,会导致树高度失衡,导致一边高,一边低,解决这样的办法可以删除左右子树最大最小节点交替实行。
或者记录一高度,主要删除,左子树或者右子树高的那一边。
代码如下:
//删除首先要找到要删除结点的位置,我一开始用的循环迭代的方法,当时发现如果删除的结点为叶节点时,不知道前面一个结点,不好删除
//于是想到递归,将要删除的这个结点地址返回给父节点,为叶节点时,直接将这个结点置空。
//找到结点后要考虑几种情况,
//1.左右还有子节点 2.左边有子节点,右边没有 3.左边没有子节点,右边有 4.左右都没有子节点(叶节点)
Tree *DeletNode(Tree **obj, Elementtype x){
if ((*obj)->val > x){//找节点
(*obj)->left = DeletNode(&((*obj)->left), x);
}
else if ((*obj)->val < x){
(*obj)->right = DeletNode(&((*obj)->right), x);
}
else{
if (obj == NULL){//没找到
printf("结点不存在\n");
}
else{//找到
if ((*obj)->left != NULL && (*obj)->right != NULL){
int x = MaxData((*obj)->left);
(*obj)->left = DeletNode(&((*obj)->left), x);//要返回给左指针,不返回,左指针还是指向原来地址,
(*obj)->val = x; //如果左边要删除的不是就是下一个还好,如果就是下一个,不返回做指针存的还是原来地址
//所以要返回
}
else if ((*obj)->left != NULL && (*obj)->right == NULL){
Tree *temp = (*obj);
(*obj) = (*obj)->left;
free(temp);
}
else if ((*obj)->left == NULL && (*obj)->right != NULL){
Tree *temp = (*obj);
(*obj) = (*obj)->right;
free(temp);
}
else{
Tree *temp = (*obj)->right;
(*obj) = NULL;
free(temp);
}
}
}
return (*obj);
}
注意:
为什么情况2/3直接等于左/右子树地址就使得上一个节点指向左/右子树,因为递归返回给了上一节点。
三.性质
二叉搜索树一个实用的性质:对二叉查找树中序遍历,遍历结果是有序的
我们直到二叉搜索树查找数值与树的高度有关,如果调整二叉查找树的形态,使得每个节点尽量有两个节点,那么二叉搜索树的高度就会很低,是得树的高度会在log(N)级别,N为节点数,能实现这一要求的数为平衡二叉树。