【数据结构初阶】--- 归并排序

归并排序

递归

递归的思路

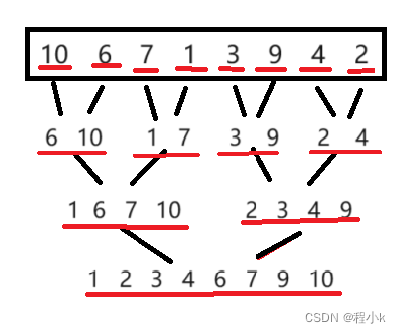
归并的前提是需要两个有序的区间，如何让整个区间变成两个有序的区间？
那就利用递归的思路，将问题分成多个子问题去解决，
想要有两个有序的区间，首先要有两个区间吧，那就从中间划分成两个区间，
想让左区间有序，那就用归并，
要归并就需要两个有序区间，那就将左区间从中间划分成两个区间，再想办法让这两个区间有序…以此类推，这个就是递归的思路

总结一下，想让一个区间有序，划分成左右区间，分别让两个区间有序，然后归并
结束条件：当这个要归并的区间只有一个值时结束

归并的步骤：

两个区间的边界：begin1,end1,begin2,end2
挨个比较两个区间的值，谁小就将谁放入临时数组中，直到一个区间拷贝完
此时另一个区间还有剩余，剩余的都比前面的值要大，所以就全部按顺序拷贝到临时数组中
将临时数组的值拷贝回原数组

代码示例

void _MergeSort(int* a, int left, int right, int* tmp)
{
	//当区间只有一个值时停止，不存在区间不存在的情况
	if (left == right)
		return;
	int mid = left + (right - left) / 2;

	//让左右两个区间都有序
	_MergeSort(a, left, mid,tmp);
	_MergeSort(a, mid + 1, right,tmp);

	//归并
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int begin = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[begin++] = a[begin1++];
		}
		else
		{
			tmp[begin++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[begin++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[begin++] = a[begin2++];
	}
	//拷贝回原数组
	memcpy(a+left, tmp+left, sizeof(int)*(right - left + 1));
				
}

//归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
	
}

非递归

快排为什么可以用栈模拟：

快排的非递归可以用栈模拟递归的过程，每次弹出区间的两个边界，从这个区间固定一个值的位置，再压入这个值的左右两个区间，这样的过程实际上模拟的是递归的前序遍历，先将本层的事做完，然后去遍历左右区间

归并可以用栈模拟吗？

不能的，因为归并排序是后序遍历的过程，先让左右区间各自有序，再进行归并操作。用栈模拟的过程中，试想一下，要让左右区间有序，所以先压右区间，再压左区间，然后要弹出栈顶元素，也就是左区间，再将这个区间的右区间、左区间压入栈中，以此类推，在过程中是没有机会进行归并操作的。

非递归的思路

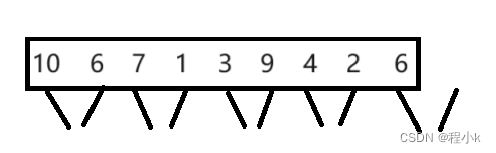
在这里插入图片描述

一一归并，两两归并，四四归并…
归并一轮就把数据拷贝回原数组，再进行下一轮归并
用gap控制每轮归并一次的数据个数，初始化gap=1，每轮结束，gap=gap*2
直到gap>n时结束（一次归并的数据个数大于n时结束）
begin1,end1,begin2,end2表示归并时数据的范围

初版代码示例

//归并非递归方法
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int begin = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[begin++] = a[begin1++];
				}
				else
				{
					tmp[begin++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[begin++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[begin++] = a[begin2++];
			}
		}
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2;
	}
}

问题：越界

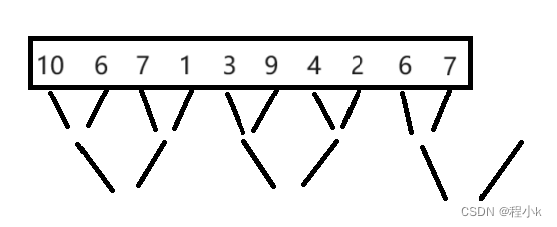
上面的情况刚好对数据的个数为2的次方时有效，如果是9个数，10个数呢，
9个数时：在第一轮归并时就会越界在这里插入图片描述
10个数时：第二轮归并时越界

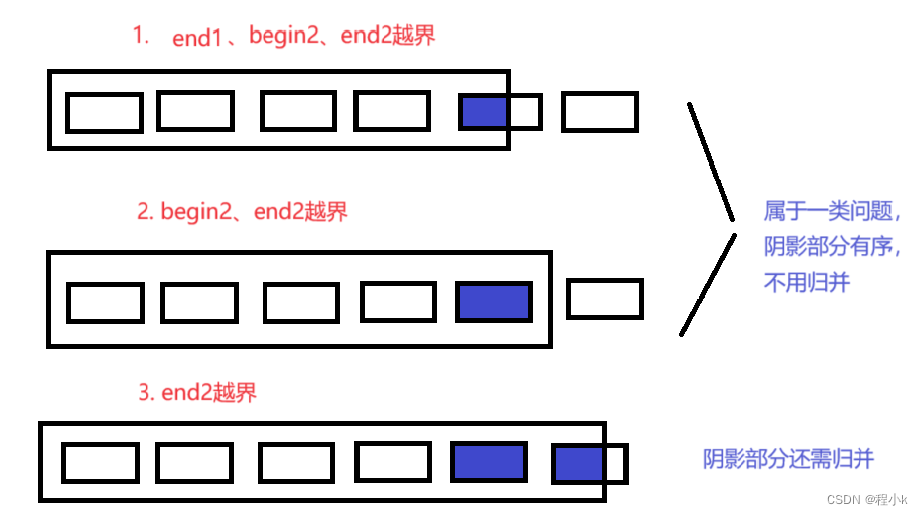
分析：

解决办法：

方法一：
每次归并前判断

if(end1 > n || begin2 > n)
{
	break;
}

如果是情况1、2，那就不用归并直接结束本轮归并，但是每轮结束后会将临时数组整体拷贝回原数组，那么没有归并的区间对应的临时数组那部分就是随机值，拷贝的时候就会用随机值覆盖原数组的这部分，为了避免覆盖，每次归并后就及时拷贝回数组，这样没归并的部分就不会被覆盖
如果是情况3，还需要归并的情况就只需把end2修改成n-1

if(end2 > n)
{
	end2 = n-1;
}

修改后的整体代码：

//归并非递归方法:每次归并后及时拷贝回原数组(解决越界)
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int begin = i;
			
			//判断越界问题
			if (end1 > n || begin2 > n)
			{
				break;
			}
			if (end2 > n)
			{
				end2 = n - 1;
			}

			//归并
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[begin++] = a[begin1++];
				}
				else
				{
					tmp[begin++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[begin++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[begin++] = a[begin2++];
			}
			//每次归并后及时拷贝回原数组
			memcpy(a+begin, tmp+begin, sizeof(int) * (end2-begin1+1));
		}
		gap *= 2;
	}
}

方法二：整体拷贝回原数组
方法一是归并一次就拷贝一次，为的是避免未归并的区域会被覆盖
想要整体拷贝还保证未归并的区域不会被覆盖，就需要将未归并的区域也先拷贝到临时数组中，然后一轮归并结束，整体拷贝回原数组
根据上面的代码知道，想将数据拷贝到临时数组中就要进入归并的操作中，如果，归并的区间一个存在，一个不存在时，还能不能进入归并的操作呢，可以的，这种情况就类似，两个区间中一个区间已经拷贝完了，另一个区间还有一部分需要拷贝到临时数组。那么现在回到越界的区域，越界的区域本质就是不存在的范围，那我们将越界的范围修改成不存在的范围，再进行归并，就可以将这未越界的部分拷贝到临时数组中，最后一轮归并结束，就可以整体拷贝回原数组了

if(end1 > n)
{
	end1 = n - 1;
	begin2 = n; //将begin2和end2修改为不存在的区间[n,n-1]
	end2 = n - 1;
}
else if(begin2 > n)
{
	begin2 = n;
	end2 = n - 1;
}
else if(end2 > n)
{
	end2 = n - 1;
}

时间复杂度

由于每次都是将区间平分成两个区间，让左区间有序，让右区间有序，再进行归并，类似递归的过程类似二叉树的结构，因此，

时间复杂度为：O(N*logN)
空间复杂度：O(N)
实际是O(N)+O(logN)
- O(N)是开辟的临时数组的大小，
- O(logN)是递归的高度，每层递归都需要建立栈帧

针对递归的优化

小区间优化

if(right - left + 1 < 10)
{
	InsertSort(a,left,right);
	return;
}

递归时，最后几层的递归调用次数占了整体的80%、90%，最后一层就占50%，所以要排的数的个数小于10个时，也就是最后三层，利用插入排序可以减少大量的递归次数，不过这种优化不会发生质的改变。