操作环境:
MATLAB 2022a
1、算法描述
差分进化算法(Differential Evolution, DE)是一种有效的实数编码的进化算法,主要用于解决实值函数的全局优化问题。本文将详细介绍差分进化算法的背景、原理、操作步骤、参数选择以及实际应用,旨在提供一个全面的理解。
1. 差分进化算法的背景
差分进化算法由Storn和Price在1997年提出,最初是为了解决Chebyshev多项式的优化问题。由于其简单、高效、易于实现等特点,DE迅速成为解决各种复杂优化问题的热门选择,尤其在工程优化、经济学、生物信息学等领域得到广泛应用。
2. 差分进化算法的原理
差分进化算法基于种群的迭代搜索。其基本思想是通过种群中个体间的差分信息引导搜索过程,通过迭代更新种群,逐渐逼近全局最优解。DE算法主要包含四个基本操作:初始化、变异、交叉和选择。
2.1 初始化
差分进化算法首先随机生成一个包含NP个D维实数向量的初始种群。每个向量代表一个潜在的解。初始种群通常在问题定义的边界内随机生成。
2.2 变异
对于种群中的每一个目标向量 𝑥𝑖,𝑔xi,g,算法通过以下公式生成一个变异向量 𝑣𝑖,𝑔+1vi,g+1:
𝑣𝑖,𝑔+1=𝑥𝑟1,𝑔+𝐹×(𝑥𝑟2,𝑔−𝑥𝑟3,𝑔)vi,g+1=xr1,g+F×(xr2,g−xr3,g)
其中,𝑟1,𝑟2,𝑟3r1,r2,r3 是从种群中随机选择的三个不同的索引,𝐹F 是缩放因子,用于控制差分扰动的幅度。
2.3 交叉
交叉操作用于增加种群的多样性。对于每个目标向量和对应的变异向量,算法按照一定的交叉概率CR进行交叉操作,生成试验向量 𝑢𝑖,𝑔+1ui,g+1:
{𝑣𝑗,𝑖,𝑔+1if 𝑟𝑎𝑛𝑑𝑗(0,1)≤𝐶𝑅 or 𝑗=𝑟𝑎𝑛𝑑(𝑖)𝑥𝑗,𝑖,𝑔otherwise{vj,i,g+1xj,i,gif randj(0,1)≤CR or j=rand(i)otherwise
其中,𝑟𝑎𝑛𝑑𝑗(0,1)randj(0,1) 是一个随机数,𝑟𝑎𝑛𝑑(𝑖)rand(i) 是一个随机选择的维度索引,保证每个试验向量至少有一个来自变异向量的分量。
2.4 选择
选择操作基于贪心策略。对于每个目标向量和对应的试验向量,如果试验向量的适应度(通常是目标函数值)优于目标向量的适应度,那么在下一代种群中替换目标向量;否则,目标向量保持不变。
3. 参数选择
差分进化算法的性能在很大程度上依赖于参数的选择,主要包括种群大小NP、缩放因子F和交叉概率CR。种群大小NP影响算法的多样性和收敛速度;缩放因子F影响搜索步长,过大可能导致过快收敛,过小可能导致收敛速度慢;交叉概率CR决定了试验向量的多样性。
4. 实际应用
差分进化算法由于其结构简单和高效性,在许多实际应用中都表现出色。例如,在工程设计中优化结构尺寸,在生物信息学中用于基因表达数据的特征选择,在金融领域优化投资组合等。
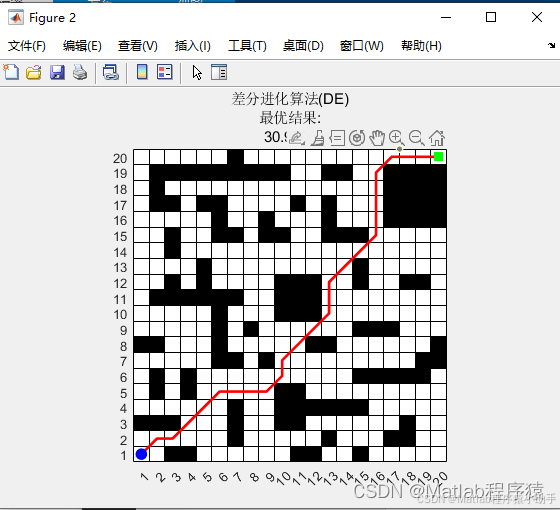
2、仿真结果演示
3、关键代码展示
略
4、MATLAB 源码获取
点击下方原文链接获取

 https://blog.csdn.net/Koukesuki/article/details/138729890?ops_request_misc=%257B%2522request%255Fid%2522%253A%25220184CDC8-B65A-45AA-B369-A4059BC2BB86%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=0184CDC8-B65A-45AA-B369-A4059BC2BB86&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-138729890-null-null.nonecase&utm_term=206&spm=1018.2226.3001.4450
https://blog.csdn.net/Koukesuki/article/details/138729890?ops_request_misc=%257B%2522request%255Fid%2522%253A%25220184CDC8-B65A-45AA-B369-A4059BC2BB86%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=0184CDC8-B65A-45AA-B369-A4059BC2BB86&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-138729890-null-null.nonecase&utm_term=206&spm=1018.2226.3001.4450