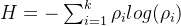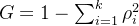1. 决策树原理介绍
通俗的理解,决策树就是对样本集根据某一个维度d和某一个阈值v进行二分,得到二叉树,即为决策树。通过样本训练计算出维度d和阈值v,即可对预测数据进行分类,如果对二叉树的各子节点value值求平均,将平均值赋予待分类样本,即完成待测样本的回归预测。
1.1 决策边界的划分
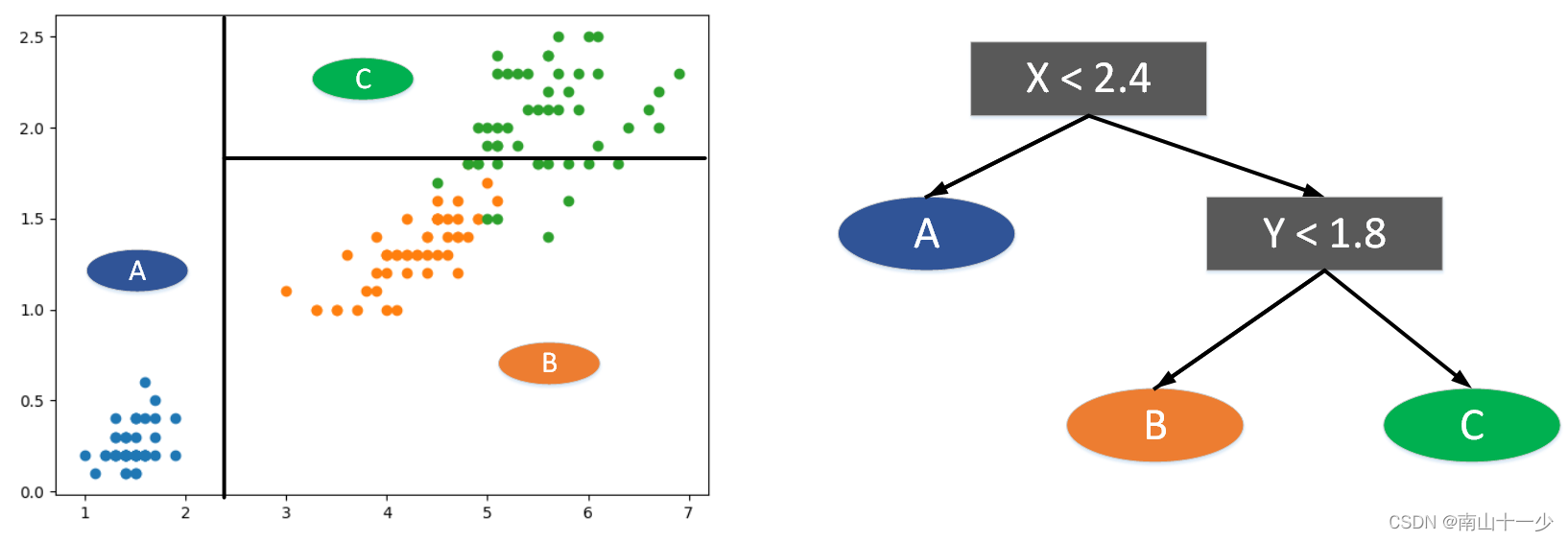
最佳阈值能够最大限度的把样本区分开,让其各自分类中单一类别比重最大,使其分类确定性更大。阈值的选取是来自特征向量相邻两个值的平均值,直观的看如上图所示。图中先以x=2.4作为分割线,小于这个阈值的完全属于A类,大于这个阈值的完全属于非A类,接下来再对非A值进行分割,以y=1.8作为分割线,小于这个阈值的属于B类比重最大,大于这个阈值的属于C类比重最大。
上述思想用代码实现如下所示,入参
X::样本输入空间
y:样本输出空间
d:分割维度
value:分割阈值
出参:
X[index_a]:分割左节点的输入空间
X[index_b]:分割右节点的输入空间
y[index_a]:分割左节点的输出空间
y[index_b]:分割右节点的输出空间
def split(X, y, d, value):
index_a = (X[:, d] <= value)
index_b = (X[:, d] > value)
return X[index_a], X[index_b], y[index_a], y[index_b]1.2 不确定性的度量
从图中可以直观的找到这个分割阈值,使其分类单一比重最大。但实际应用中, 如何找到这个阈值,我们是否有一个可以量化的评判标准呢?
可以通过信息熵和基尼系数量化的评判每一次分割对样本集的确定性进行度量,单一性越好,能够最大限度的分开两个类别,其信息熵和基尼系数值越小,否则越大。我们可以通过网格搜索的思想,对所有样本各个维度的分割点进行信息熵或基尼系数的计算,找到最小值,从而确定每个节点在哪个维度做划分,某个维度在哪个值上做分割。
信息熵的公式如下:
基尼系数的公式如下:
如果某一分割线能够完全将样本中的某一类别区分开,即某节点中的类别单一性最佳,确定度最大,为100%纯单一类别。根据以上公式可得信息熵和基尼指数值均为0。使用代码表示以上公式如下所示:
def entropy(y):
counter = Counter(y)
res = 0.0
for num in counter.values():
p = num / len(y)
res += -p * log(p)
return res
def gini(y):
counter = Counter(y)
res = 1.0
for num in counter.values():
p = num / len(y)
res -= p**2
return res1.3 决策边界的寻找
通过阈值对样本分类后,可将分类中的输出空间代入以上方法入参,即可计算得出此分类样本左右节点的信息熵或基尼系数。
假如先以x轴特征向量为判断条件,将所有样本横坐标从小到大依次排列,所有相邻两个样本值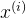
的中值
依次作为阈值分别进行分割,计算分割后两个类别(左右节点数据集)的信息熵或基尼系数。同理,以y轴特征向量为判断条件,依次计算信息熵或基尼系数。最后,将左右节点的信息熵或基尼系数相加,遍历所有维度所有阈值,找到最小值。此时的维度和阈值作为分隔点分割出A类和非A类,然后用同样的方法对非A类再进行分隔,得到B类和C类。
值得注意的是,先以x轴还是y轴进行分隔,最后的决策边界可能完全不同,因其分割线只能是某个向量的值,有可能在多个维度上寻找到相同的最小值,又因决策树无法在一次分隔中同时兼顾多个向量,所以导致最后的决策边界会因遍历维度的先后顺序不同而不同。其具体代码实现如下:
def try_split(X, y):
best_entropy = float('inf')
best_d, best_v = -1, -1
for d in range(X.shape[1]): # 列,维度,特征 数量
sorted_index = np.argsort(X[:, d])
for i in range(1, len(X)):
if X[sorted_index[i], d] != X[sorted_index[i - 1], d]:
v = (X[sorted_index[i], d] + X[sorted_index[i - 1], d]) / 2
X_l, X_r, y_l, y_r = split(X, y, d, v)
e = entropy(y_l) + entropy(y_r)
if e < best_entropy:
best_entropy, best_d, best_v = e, d, v
return best_entropy, best_d, best_v1.4 自编决策树的验证
以鸢尾花数据集为例,根据上述方法,进行试验,进行深度为2的切割,数据准备及相关包引入代码:
import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from collections import Counter
from math import log
# 鸢尾花数据集准备
def dataInit(type="iris"):
if type == "iris":
iris = datasets.load_iris()
X = iris.data[:, 2:] # 使用后两个特征
y = iris.target # 三分类
elif type == "boston":
data_url = "http://lib.stat.cmu.edu/datasets/boston"
boston = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([boston.values[::2, :], boston.values[1::2, :2]])
target = boston.values[1::2, 2]
X, y = data, target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
return X_train, X_test, y_train, y_test, X, y首先对样本集进行第一层二叉分割,由于左节点信息熵和基尼系数为0,故不需要对左节点进行第二层划分,右节点基尼系数为0.69,还比较偏大,进行第二次划分,代码实现如下所示:
def myDecisionTree():
X = dataInit(type="iris")[4]
y = dataInit(type="iris")[5]
# 第一个节点的阈值的计算
best_entropy, entropy_left, entropy_right, best_d, best_v = try_split(X, y)
print("第一个节点的阈值的计算 best_entropy = {},entropy_left = {} ,entropy_right = {}, best_d = {}, best_v = {}".format(
best_entropy, entropy_left, entropy_right, best_d, best_v))
# 根据阈值切分第一层左右子节点
X1_left, X1_right, y1_left, y1_right = split(X, y, best_d, best_v)
# 对第一层右节点进行二次分类,并计算其分类阈值
best_entropy2, entropy_left2, entropy_right2, best_d2, best_v2 = try_split(X1_right, y1_right)
print("第二个节点的阈值的计算 best_entropy2 = {},entropy_left2 = {} ,entropy_right2 = {}, best_d2 = {}, best_v2 = {}".format(
best_entropy2, entropy_left2, entropy_right2, best_d2, best_v2))
# 根据阈值切分得到第二层左右子节点
X2_left, X2_right, y2_left, y2_right = split(X1_right, y1_right, best_d2, best_v2)2. 基于sklearn的决策树实现
上述是通过决策树的原理进行手敲代码实现,但在实际应用中,笔者还是建议使用sklearn封装的方法进行实现,手敲决策树只是为了方便读者理解其实现原理,封装的代码做了更多的性能优化和超参数设置。具体代码如下:
def decisionTreeClassification():
# 基于信息熵的决策树分类
X_train, X_test, y_train, y_test, X, y = dataInit(type="iris")
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy", random_state=42)
dt_clf.fit(X_train, y_train)
train_score = dt_clf.score(X_train, y_train)
test_score = dt_clf.score(X_test, y_test)
print("基于信息熵的决策树分类 训练集得分 = {}, 测试集得分 = {}.".format(train_score, test_score))
# 基于基尼系数的决策树分类
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="gini", random_state=42)
dt_clf.fit(X_train, y_train)
train_score = dt_clf.score(X_train, y_train)
test_score = dt_clf.score(X_test, y_test)
print("基于基尼系数的决策树分类 训练集得分 = {}, 测试集得分 = {}.".format(train_score, test_score))
决策树解决回归问题,以房价数据集为例,调用方法如下所示:
# 决策树回归
def decisionTreeRegression():
X_train, X_test, y_train, y_test, X, y = dataInit(type="boston")
dt_reg = DecisionTreeRegressor()
dt_reg.fit(X_train, y_train)
train_score = dt_reg.score(X_train, y_train)
test_score = dt_reg.score(X_test, y_test)
print("决策树回归 训练集得分 = {}, 测试集得分 = {}.".format(train_score, test_score))3. 决策树常用超参数介绍
3.1 DecisionTreeClassifier的参数
-criterion:衡量分割质量的指标。默认为"gini"表示基尼系数,也可以设置为entropy表示信息熵
-splitter:选择分裂节点的策略。默认为"best"表示最优分裂,也可以设置为random"表示随机分裂
-max_depth:树的最大深度。默认为 None 表示不限制树的深度,也可以设置为整数来限制树的深度
-min_samples_split :分裂节点所需的最小样本数。默认为2,表示至少需要2个样本才能进行分裂,可以设置为整数或浮点数来调整这个值。
-min_samples_leaf:叶子节点所需的最小样本数。默认为1,表示叶子节点至少需要一个样本,可以设置为整数或浮点数来调整这个值。
-min_weight_fraction leaf:叶子节点的最小权重比例。默认为0,表示不考虑叶子节点的权重,可以设置为浮点数来调整这个值
-max_features:每个节点分裂时考虑的特征数。可以设置为整数或浮点数,表示考虑的特征数目或比例。默认为"auto"表示考虑所有特征
-random state:随机种子。如果设置了随机种子,每次练都会得到相同的结果。默认为 None,表示使用系统默认的随机种子
-maxleaf_nodes:最大叶子节点数。默认为None,表示不限制叶子节点数目,可以设置为整数来限制叶子节点数目
-class_weight:类别权重。可以设置为"balanced"表示根据训练样本自动调节类别权重,也可以设置为一个字典来指定每个类别的权重
-ccp_alpha:剪枝系数。默认为 0,表示不剪枝,可以设置为一个非负浮点数来进行剪枝。
3.2 DecisionTreeRegressor的参数
-criterion:这个参数指定了决策树的分裂策略, {“squared_error”平均平方误差, “friedman_mse”平均平方误差与Friedman改进得分, “absolute_error”平均绝对误差, “poisson”减少泊松偏差}, default=”squared_error”
-splitter:这个参数指定了决策树的分裂策略,可以选择“best”(最优)或“random”(随机)。
-max_depth:这个参数指定了决策树的最大深度,用于控制决策树的复杂度
-min_samples_split:这个参数指定了最小分裂样本数,用于控制决策树的分裂策略。
-min samples_leaf:这个参数指定了最小叶子节点样本数用于控制决策树的剪枝策略
-max_features:这个参数指定了每个节点可选的特征数,用于控制决策树的复杂度和泛化能力。
-random_state:这个参数指定了随机种子,用于控制每次运行的结果是否一致。
4 总结
本文讲解了决策树的原理以及信息熵和基尼系数对决策树分类的作用,并通过手写代码进一步阐述了决策树的实现原理。最后通过调用sklearn封装的函数使用决策树算法解决分类及回归问题,以及函数中诸多超参数的含义。