Bootstrap

数据结构C语言描述1(图文结合)--顺序表讲解，实现，表达式求值应用，考研可看

前言

  • 这个专栏将会用纯C实现常用的数据结构和简单的算法；
  • 用C基础即可跟着学习，代码均可运行；
  • 准备考研的也可跟着写，个人感觉，如果时间充裕，手写一遍比看书、刷题管用很多，这也是本人采用纯C语言实现的原因之一；
  • 欢迎收藏 + 关注，本人将会持续更新。

顺序表基本概念

什么是线性表？

线性表是一组具有相同特征元素的有序序列，记作：（a1, a2, …, ai-1, a！, ai+1, …, an），当然这有点官方了，但是核心就两个特征：相同特征、有序序列；但我从《大话数据结构中》中看到了另外一个描述，我感觉听通俗易懂的：

  • 线性表的数据对象集合{a1, a2, …, ai-1, a！, ai+1, …, an}，每个元素的类型均为DataType。其中，除了第一个元素a1 外，每一个元素有且只有直接前驱元素，除了最后一个元素an 外，每一个元素有且只有一个直接后驱元素。且数据元素之间关系是一一对应的。

线性表相关概念

  • 直接前驱元素：ai-1 领先于ai ，则称ai-1 是ai 的直接前驱元素；
  • 直接后驱元素：ai+1 领先于ai ，则称ai+1 是ai 的直接后驱元素；
  • 前驱元素：a1,a2,a3,……ai-1, 都是ai 的前驱元素；
  • 后驱元素：ai+1,ai+2,ai+3,……ai+n, 都是ai 的前驱元素；
  • 线性表长度：线性表中包含所有元素的个数；
  • 空线性表：不包含任何元素的线性表；
  • 位序：元素在线性表第几个位置

什么是顺序表？

顺序表就是用一段连续的内存空间依次存储数据，顺序表的存储大概图如下(参考《大话数据结构》)：

在这里插入图片描述

顺序表特点

  • 存储数据内存地址连续
  • 可以支持下标访问
  • 删除、添加中间位置元素麻烦
  • 数据容量固定

顺序表的抽象设计

把顺序表存储的东西，看成是一个集合中存储，从**抽象数据类型(ADT)**角度来看，这个我们需要数据的实现可以有一下几个基本操作：

  • 创建、初始化循序表
  • 插入元素
  • 删除元素
  • 查找元素
  • 判空操作
  • 判满操作

总之一句话：增删改查外加排序。

顺序表程序实现

封装顺序表

  • 对数据类型进行取别名，这样是代码更具有泛化性；
  • 采用结构体进行封装，可以更好描述顺序表
typedef int DataType;

typedef struct SeqList {
	DataType* data;     // 储存数据
	size_t size;	   // 当下储存了多少数
	size_t capacity;   // 当下能够储存数据的最大容量
}SeqList;

创建顺序表

利用calloc函数，他会在申请内存的时候自动初始化为空，这里具体他做了一下几件事情：

  • 事情一块内存空间，大小为sizeof(Seqlist)
  • data = NULL
  • size = 0
  • capacity = 0
SeqList* create_seqlist()
{
	SeqList* new_data = (SeqList*)calloc(1, sizeof(SeqList));
	if (!new_data) {
		printf("顺序表创建失败\n");
		return new_data;
	}

	return new_data;
}

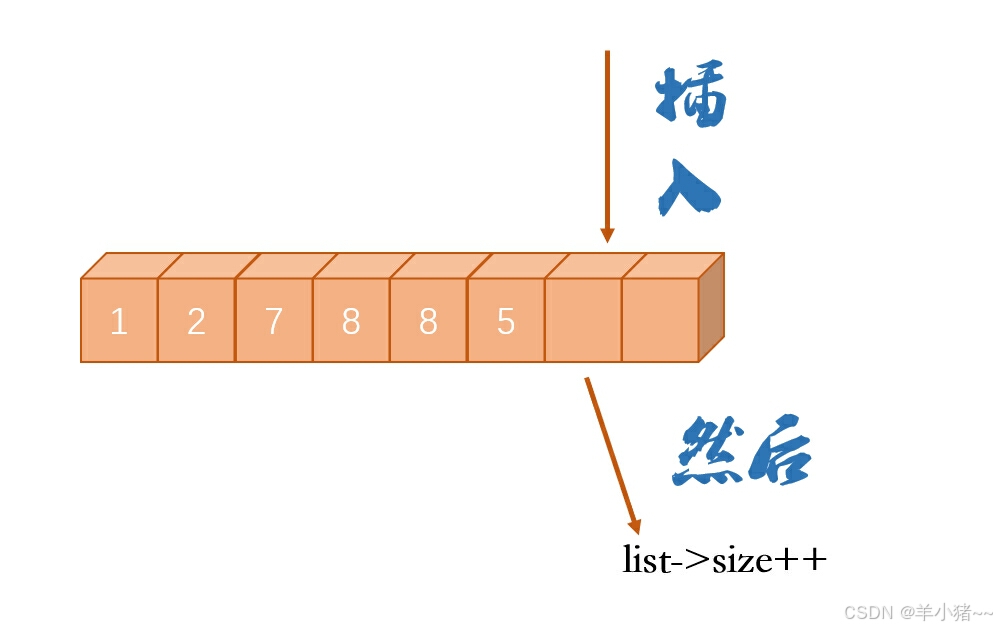
插入元素

这里是向后插入，扩容规则如下(自己定义的，不是一定的)：

  • 如果capacity为0，则赋值为10，当作初始化
  • 否则如果容量不够，则按照两倍扩容

向后插入图示如下(也可以有序插入，这个需要按照具体场景)：

在这里插入图片描述

void insert_seqlist(SeqList* list, DataType data)
{
	assert(list);   // list为空，则断言

	// 是否需要扩容
	if (list->size >= list->capacity) {
		// 2倍扩容
		if (list->capacity == 0) {
			list->capacity = 10;
		}
		else {
			list->capacity = 2 * list->capacity;
		}
		// 扩容
		DataType* new_data = (DataType*)realloc(list->data, list->capacity * sizeof(DataType));
		assert(new_data);  // 判断内存是否申请失败
		list->data = new_data;
	}

	// 直接在后面插入，但是也可以有序插入，这个要根据业务
	list->data[list->size++] = data;
}

查找–按值查找

  • 目的：通过值找到返回他在顺序表中的存储的下标，规则：如果改顺序表中不存在该元素，则返回-1。
  • 方法：遍历，从第一个遍历到最后，时间复杂度为O(n)
int search_value_seqlist(SeqList* list, DataType data)
{
	// 防止空表
	assert(list);

	for (size_t i = 0; i < list->size; i++) {
		if (list->data[i] == data) {
			return i;
		}
	}
		
	return -1;  
}

查找–按位查找

  • 目的：通过下标找到返回他在顺序表中的存储的元素，规则：如果传递位有误，则返回-1。
DataType search_position_seqlist(SeqList* list, size_t k)
{
	assert(list);

	if (k >= list->size || k < 0) {
		return -1;
	}

	return list->data[k];
}

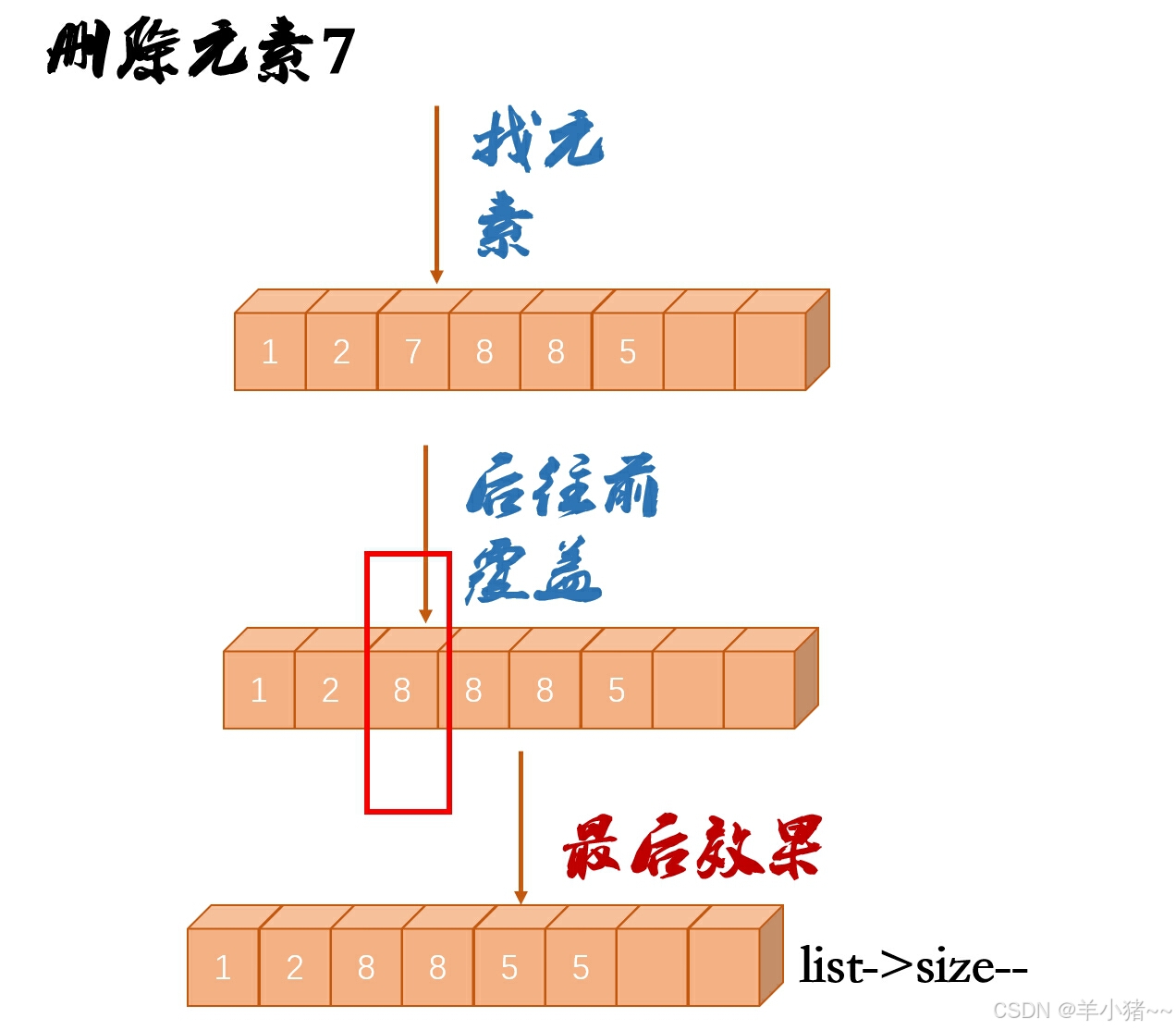
删除–通过下标

  • 目的：删除下标为k的元素
  • 数组的删除为伪删除，不是真正的删除，将删除的元素移动到最后而已，具体过程图示如下：

在这里插入图片描述

void erase_seqlist_index(SeqList* list, size_t index)
{
	assert(list);

	if (index < 0 || index >= list->size) {
		printf("无效位置\n");
		return;
	}

	for (int i = index; i < list->size - 1; i++) {
		list->data[i] = list->data[i + 1];
	}

	list->size--;
}

删除–通过指定元素

  • 删除第一个符合元素，具体过程如图示(和上图一样)：

在这里插入图片描述

void erase_seqlist_data(SeqList* list, DataType data)
{
	assert(list);

	for (size_t i = 0; i < list->size; i++) {
		if (list->data[i] == data) {
			erase_seqlist_index(list, i);   // 原理一样
		}
	}
}
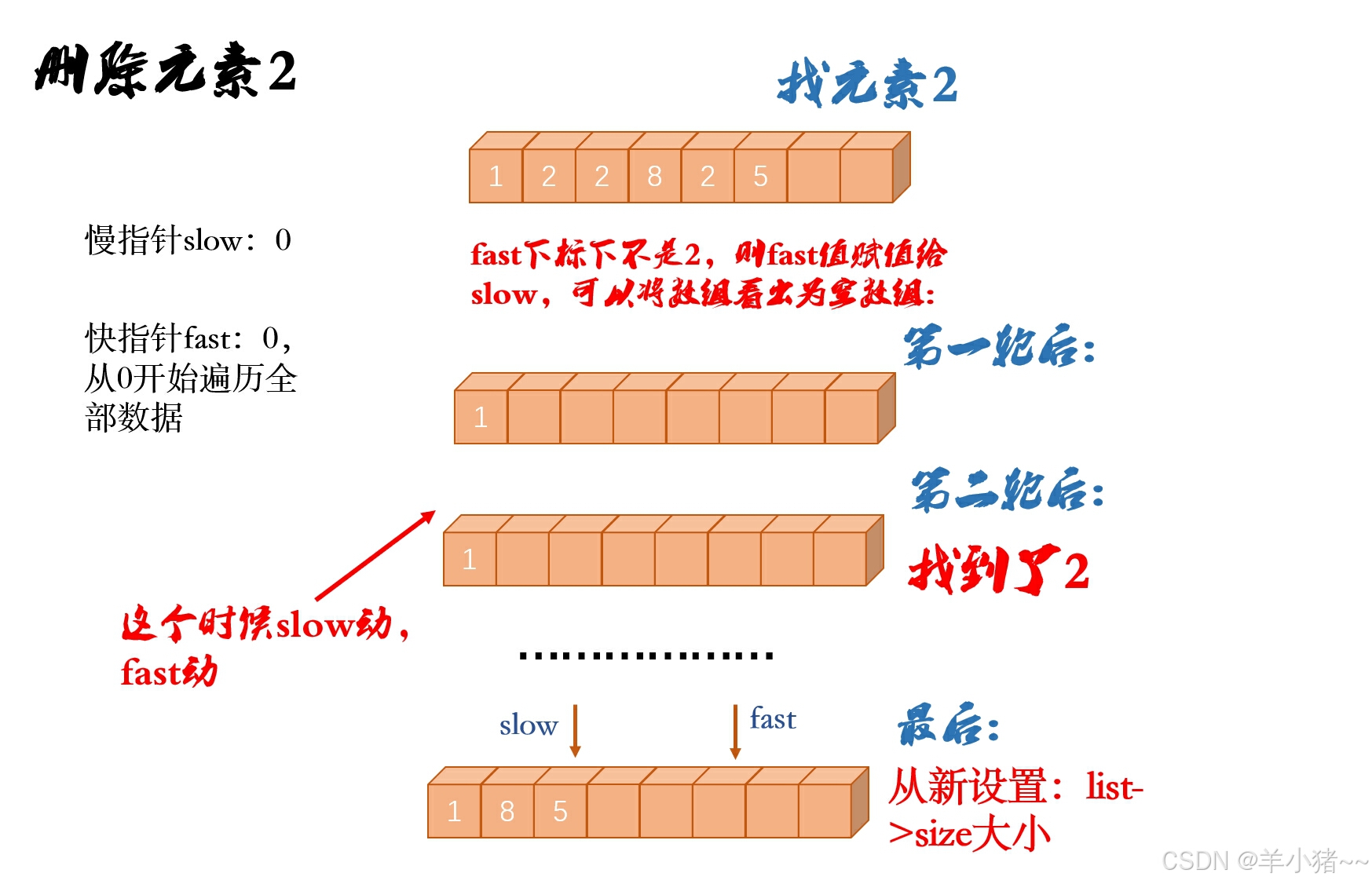
  • 删除全部符合元素删除，采用双指针算法，最快理解就是通过图示，如下：

在这里插入图片描述

void erase_seqlist_all(SeqList* list, DataType data)
{
	assert(list);

	// 第一种方法：暴力，这里不写

	// 第二种方法: 双指针
	size_t slow = 0, fast = 0;
	int num = 0;
	for (; fast < list->size; fast++) {
		if (list->data[fast] == data) {
			num++;
			continue;
		}
		else {
			list->data[slow++] = list->data[fast];
		}
	}
	list->size -= num;
}

判断是否为空

判断链表是不是没有存储元素，但是要注意，没有存储元素只是代表SeqList->size==0，但不代表数组里没有储存元素，没有内容空间，具体为什么，可以想一想？？？？

bool emtpy_seqlist(SeqList* list) {
	return list->size == 0;
}

查询顺序表大小

查找当前顺序表中储存元素的数量

int size_seqlist(SeqList* list) {
	return list->size;
}

销毁

释放顺序表，将申请的内存空间全部释放：

  • 第一步：释放数据空间
  • 第二步：释放创建的顺序表

注意：释放完毕后，指针需要赋值为NULL

void destory_seqlist(SeqList* list)
{
	assert(list);

	// 释放数据
	if (list->data != NULL) {
		free(list->data);
		list->data = NULL;
	}
	// 释放链表
	free(list);
	list = NULL;
}

总代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

// 增删改查外加排序

typedef int DataType;

typedef struct SeqList {
	DataType* data;
	size_t size;
	size_t capacity;
}SeqList;

// 创建顺序表
SeqList* create_seqlist();

// 插入
void insert_seqlist(SeqList* list, DataType data);

// 查找--按值查找，找得到则返回下标(0开始)，找不到就返回-1
int search_value_seqlist(SeqList* list, DataType data);
// 查找--按位查找，越界：-1，正常：下标
DataType search_position_seqlist(SeqList* list, size_t k);

// 删除--通过下标(位置), index从0开始
void erase_seqlist_index(SeqList* list, size_t index);
// 删除--通过指定元素
void erase_seqlist_data(SeqList* list, DataType data);  // 删除一个
void erase_seqlist_all(SeqList* list, DataType data);   // 删除全部

// 万金油函数
bool emtpy_seqlist(SeqList* list) {
	return list->size == 0;
}
int size_seqlist(SeqList* list) {
	return list->size;
}

// 打印
void print_seqlist(SeqList* list);

// 销毁
void destory_seqlist(SeqList* list);

int main()
{
	SeqList* list = create_seqlist();

	for (int i = 0; i < 15; i++) {
		insert_seqlist(list, i);
	}
	insert_seqlist(list, 8);
	printf("插入测试：\n");
	print_seqlist(list);
	printf("查找测试：\n");
	DataType value = search_value_seqlist(list, 8);
	int pos = search_position_seqlist(list, 2);
	printf("from_value: %d, from_pos: %d\n", value, pos);
	printf("删除测试: \n");
	erase_seqlist_index(list, 5);  
	print_seqlist(list);
	erase_seqlist_data(list, 9);
	print_seqlist(list);
	erase_seqlist_all(list, 8);
	print_seqlist(list);
	printf("万金油函数: \n");
	printf("是否为空：%d\n", emtpy_seqlist(list));
	printf("大小: %d\n", size_seqlist(list));
	// 销毁
	destory_seqlist(list);

	return 0;
}

SeqList* create_seqlist()
{
	SeqList* new_data = (SeqList*)calloc(1, sizeof(SeqList));
	if (!new_data) {
		printf("顺序表创建失败\n");
		return new_data;
	}

	return new_data;
}

void insert_seqlist(SeqList* list, DataType data)
{
	assert(list);   // list为空，则断言

	// 是否需要扩容
	if (list->size >= list->capacity) {
		// 2倍扩容
		if (list->capacity == 0) {
			list->capacity = 10;
		}
		else {
			list->capacity = 2 * list->capacity;
		}
		// 扩容
		DataType* new_data = (DataType*)realloc(list->data, list->capacity * sizeof(DataType));
		assert(new_data);  // 判断内存是否申请失败
		list->data = new_data;
	}

	// 直接在后面插入，但是也可以有序插入，这个要根据业务
	list->data[list->size++] = data;
}

void print_seqlist(SeqList* list)
{
	for (size_t i = 0; i < list->size; i++) {
		printf("%d ", list->data[i]);
	}
	puts("\n");
}

int search_value_seqlist(SeqList* list, DataType data)
{
	// 防止空表
	assert(list);

	for (size_t i = 0; i < list->size; i++) {
		if (list->data[i] == data) {
			return i;
		}
	}
		
	return -1;  
}

DataType search_position_seqlist(SeqList* list, size_t k)
{
	assert(list);

	if (k >= list->size || k < 0) {
		return -1;
	}

	return list->data[k];
}

void erase_seqlist_index(SeqList* list, size_t index)
{
	assert(list);

	if (index < 0 || index >= list->size) {
		printf("无效位置\n");
		return;
	}

	for (int i = index; i < list->size - 1; i++) {
		list->data[i] = list->data[i + 1];
	}

	list->size--;
}

void erase_seqlist_data(SeqList* list, DataType data)
{
	assert(list);

	for (size_t i = 0; i < list->size; i++) {
		if (list->data[i] == data) {
			erase_seqlist_index(list, i);   // 原理一样
		}
	}
}

void erase_seqlist_all(SeqList* list, DataType data)
{
	assert(list);

	// 第一种方法：暴力，这里不写

	// 第二种方法: 双指针
	size_t slow = 0, fast = 0;
	int num = 0;
	for (; fast < list->size; fast++) {
		if (list->data[fast] == data) {
			num++;
			continue;
		}
		else {
			list->data[slow++] = list->data[fast];
		}
	}
	list->size -= num;
}

void destory_seqlist(SeqList* list)
{
	assert(list);

	// 释放数据
	if (list->data != NULL) {
		free(list->data);
		list->data = NULL;
	}
	// 释放链表
	free(list);
	list = NULL;
}

顺序表案例

顺序表应用常见有很多， 比如说：储存数据(管理系统等)，这里我们做一个多项式合并，多项式次数存储有序，次数从高到低。

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

#define max_num 100

typedef struct Node {
	int data;   // 底数
	int exp;    // 指数
}Node;

typedef struct SeqList {
	Node data[max_num];
	int count;
}SeqList;

void add(SeqList* A, SeqList* B, SeqList* C)
{
	if (A == NULL || B == NULL || C == NULL) {
		return;
	}

	int i = 0, j = 0, k = 0;
	while (i < A->count && j < B->count) {
		// 次数对比
		if (A->data[i].exp > B->data[j].exp) {
			C->data[k++] = A->data[i++];
		}
		else if (A->data[i].exp < B->data[j].exp) {
			C->data[k++] = B->data[j++];
		}
		else {  // 次数相同
			Node t;
			if (A->data[i].data + B->data[j].data == 0) {
				continue;
			}
			t.exp = A->data[i].exp;
			t.data = A->data[i++].data + B->data[j++].data;
			C->data[k++] = t;
		}
		C->count++;
	}

	while (i < A->count) {
		C->data[k++] = A->data[i++];
	}

	while (j < B->count) {
		C->data[k++] = B->data[j++];
	}

}

int main()
{
	// y = 3 * x^2 + 5 * x + 2
	SeqList A = { {{3, 2},{5,1},{2, 0}}, 3 };
	// y = -1 * x^3 + 4 * x^2 + 4
	SeqList B = { {{-1,3},{4, 2},{4, 0}}, 3 };

	SeqList C = { 0 };  // 答案

	add(&A, &B, &C);

	int i = 0;
	while (i < C.count) {
		if (C.data[i].exp == 0) {
			printf("%d ", C.data[i].data);
		}
		else {
			printf("%d * x^%d ", C.data[i].data, C.data[i].exp);
		}

		if (i != C.count - 1) {
			printf("+ ");
		}
		i++;
	}


	return 0;
}

// 输出：
/*
-1 * x^3 + 7 * x^2 + 5 * x^1 + 6
*/

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
数仓之新零售项目
Python爬虫入门实战之猫眼电影数据抓取(理论篇)
分享几个echarts复杂结构和图例字体中数字显示不同颜色
阅读Skeleton-Based Action Recognition with Shift Graph Convolutional Network(CVPR2020)
el-input设置placeholder字体大小
Docker 的数据管理、镜像的创建
omnet++安装 osgEarth步骤详解（ubuntu20.04）
基于tomcat支持完成的WebScoket实现（一对一，一对多聊天）
《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》DIOU论文
「漏洞复现」鲸发卡系统 /pay/xinhui/request_post 任意文件读取漏洞
;