经典排序算法复习

分类

• 交换类

  • 冒泡
  • 快排

• 分配类

  • 计数排序
  • 基数排序

• 选择类

  • 选择排序

  • 堆排序

• 归并类

  • 归并排序

• 插入类

  • 直接插入排序

  • 希尔排序

  • 折半插入排序

冒泡排序

基于交换。每一轮找最大值放到数组尾部

//冒泡排序
void bubSort(int* arr,int size){
	bool sorted=false;
	while(size--&&!sorted){
		sorted=true;//检查某一趟排序是否已完全排好
		for(int i=0;i<size;i++){
			// printf("下标为%d的元素和%d的元素正在比较\n",i,i+1);
			if(arr[i+1]<arr[i]) {
				swap(&arr[i+1],&arr[i]);
				sorted=false;
			}
		}
	// printf("第%d趟已比完\n",size);
	}
}

1. 比较趟数是size-1次,for循环体循环次数为"当前的size"次,即每趟比较次数

2. sorted提高代码效率,只要排好序就不需再进入下一趟排序

快速排序

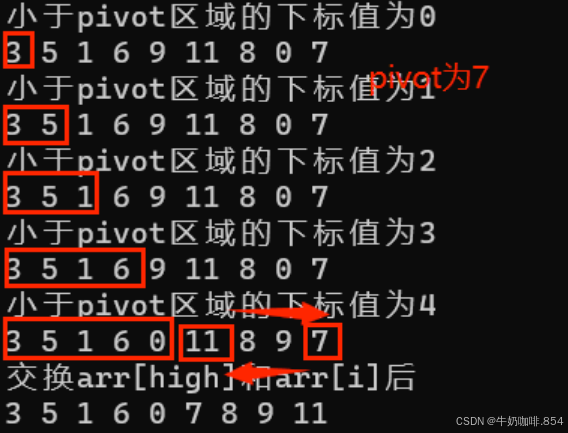
冒泡排序优化版本，每趟将数分为大于某基准和小于某基准的两部分

//快速排序之分区
int partition(int* arr, int low, int high) { //->返回pivot下标
	int pivot = arr[high];//用low下标值做pivot
	int i = low, j;
	for (j=low; j < high; j++) {
		if (arr[j] < pivot) {
			swap(&arr[i], &arr[j]);//将小于pivot的元素交换到左侧
			i++;//大于pivot区域的第一个下标加1
			printf("大于pivot区域的第一个下标值为%d\n", i);
		}
	}
	swap(&arr[i], &pivot);//把pivot归位
	return i;
}
void QuickSort(int* arr, int low,int high) {
	if (low >= high) return;
	int p=partition(arr, low, high);
	QuickSort(arr, low, p - 1);
	QuickSort(arr, p + 1, high);
}

1. i-1为已确定的小于pivot区域的下标值

2. 传参high=size-1,否则越界

归并排序

二路归并，递归实现

//归并排序之两数组合并
void merge(int* arr, int low, int mid, int high) {
	//创建临时数组
	int* tmp_arr = (int*)malloc(sizeof(int) * (high - low + 1));
	int i = low, k = low;
	int j = mid + 1;
	while (i<=mid&&j<=high)//[low---mid]/ [mid+1---high]两个数组
		tmp_arr[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
	while (i <= mid) tmp_arr[k++] = arr[i++];
	while (j <= high) tmp_arr[k++] = arr[j++];
	//复制到原数组
	for (i = low,k=0; i <= high; i++,k++)
		arr[i] = tmp_arr[k];
}
void MergeSort(int* arr, int low, int high) {
	if (low >= high) return;
	int mid = (high + low) / 2;
	//分
	MergeSort(arr, low, mid);
	MergeSort(arr, mid + 1, high);
	//治
	merge(arr, low, mid, high);
}

1. 递归“分”，再依次“治”；分只需两个参数low和high，“治”需三个参数，即两个子数组
2. 递归出口：low>=high而不是low>high
3. 每次将此次将排好序的数放到原区间内，每次动态开辟tmp_arr数组空间

堆排序

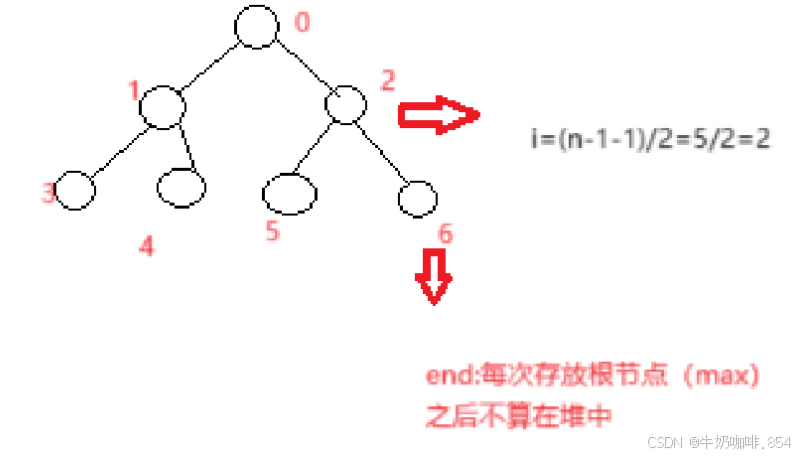
• 大根堆：父亲的权值比左右子树权值大
• 孩子结点下标编号：2i ,2i+1
  

typedef struct Heap{
	int* root;
	int length;
}Heap;
Heap* CreateHeap(int length){
	Heap* heap=(Heap*)malloc(sizeof(Heap));
	assert(heap);
	heap->
}
void pushHeap(Heap* heap,int arr);
int popHeap(Heap* heap);
//伪代码
for(arr){
	pushHeap(heap,arr[i]);
}
for(heap){
	arr[i]=pop(heap)
}
//不定义结构体
void sift(int* array, int low, int high) {
	int parent = low, child = 2 * parent + 1;//即为左孩子
	int tmp = array[parent];//当前需要调整的树的根节点
	while (child <= high) {
		//child+1 <= high为防止数组越界
		if (child+1 <= high && array[child] < array[child + 1]) child = child +1;//存大孩子节点编号
		if (tmp < array[child]) {
			array[parent] = array[child];
			parent = child; child = 2 * parent +1;//继续向下遍历
		}
		else break;
	}
	array[parent] = tmp;
}
void HeapSort(int* array, int size) {
	int i;//非叶子结点的最大编号
	for (i = (size-1-1) / 2; i >= 0; i--) {
		sift(array, i, size-1);
	}//建大根堆
	for (i = size-1; i >= 1; i--) {//循环n-1次完成堆排序
		swap(&array[0],&array[i]);
		// int tmp = array[0];
		// array[0] = array[i];
		// array[i] = tmp;
		sift(array, 1, i - 1);
	}
}

1. sift参数为low,high,high可以取到且为size-1
2. 大根堆建立的基础是孩子也为大根堆,所以从后往前依次建堆
3. 最大数移到数组最后则表示其出堆,high-1

插入排序

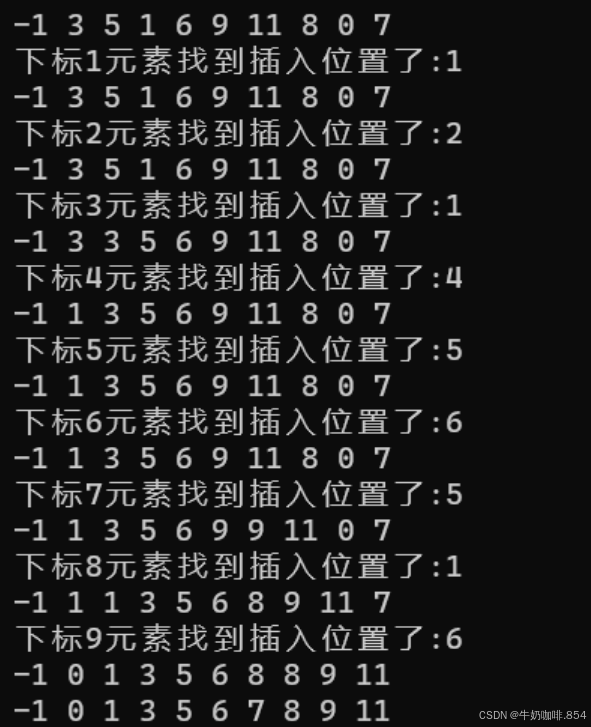
把无序区的元素插入到有序区对应的位置

//直接插入排序(从小到大排)
void insert_sort(int* array, int size) {
	int j,tmp;
	for (int i = 1; i < size; i++) {//n趟
		tmp = array[i];
		int end = i-1;
		for (; end >= 0; end--) {//每趟比较次数因数据有序程度而变化，最坏是i次，则移动次数最坏是i+2次
			if (tmp < array[end]) array[end + 1] = array[end];
		
			else break;//如果大于等于,跳出循环!!!!end不能再--
		}
		printf("下标%d元素找到插入位置了:%d\n",i,end+1);
		printArray(array,size);
		array[end+1] = tmp;
	}
}

1. 找end位置,找到就跳出循环!! else break;如果不加end每次循环到1
2. end+1<size 防止数组越界
3. end+1为第i个节点的插入位置