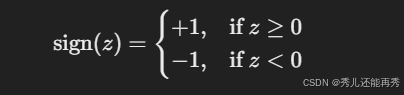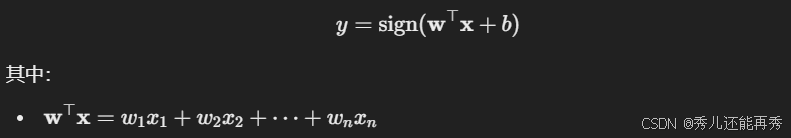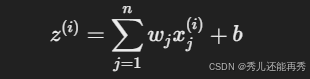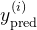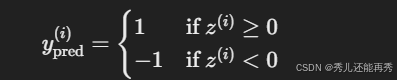此前篇章：

神经网络中常用的激活函数

神经网络（系统性学习一）：入门篇

单层神经网络（又叫感知机）

单层网络是最简单的全连接神经网络，它仅有输入层和输出层，没有隐藏层。即，网络的所有输入直接影响到输出。

结构：输入层 → 输出层

特点：

• 只适用于线性可分问题。即，单层网络只能学习并解决线性可分的问题（例如，二维平面上的两类点可以通过一条直线分开）。

• 单层感知机的输出由输入的加权和经过激活函数（如sigmoid）产生。

优点：结构简单，计算量较小。

缺点：无法解决非线性问题，如XOR问题（异或问题）。因为单层网络只能找到线性决策边界，无法处理更复杂的模式。

详细讲解

感知机最初设计用于二分类问题，用来判断输入样本属于正类还是负类。

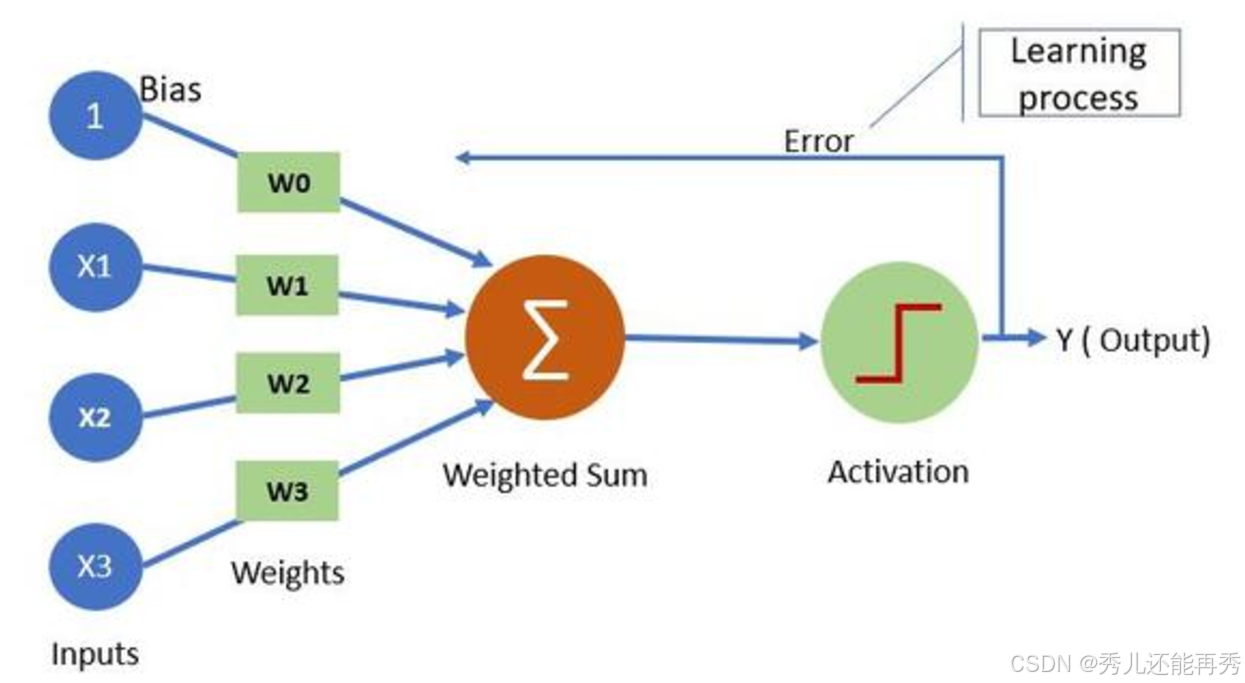
1、模型结构：

感知机的输入：

• 输入特征向量：

• 权重向量：

• 偏置：b

通常，我们还有一个0项权重，或者说常数项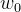 ，即对应的权重。这里我们忽略这一非重点的常数项。

加权和：感知机通过将输入特征与权重进行加权求和，再加上偏置项，得到一个总和值。

激活函数：通常是符号函数sign（z）

感知机模型的输出为：

2、基本步骤

感知机的学习过程是个迭代优化过程，通过不断调整权重和偏置，使模型能够正确分类训练数据。

1、初始化权重和偏置：

在训练开始前，感知机的权重 w1,w2,...,wn 和偏置 b 通常被初始化为小的随机值，或者初始化为零。学习率 η也是一个超参数，通常设置为一个小的正数，如 0.01 或 0.1。

2、对每一个样本计算加权和：

3、通过激活函数预测样本分类标签

4、误差计算与权重更新（反向传播）：

对于每一个样本，如果预测分类结果正确，则不更新权重和偏置。否则利用预测误差更新权重和偏置：

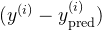
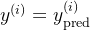
这里的更新规则是通过误差来调整权重和偏置。如果分类正确（即 ，则权重和偏置不发生变化。

5、迭代过程（epoch）

对于每个训练样本，逐个计算加权和、应用激活函数、更新权重和偏置。每一轮迭代，会对所有训练样本进行一次更新。通常需要多轮迭代才能训练出一个合适的模型。

停止条件为：

• 达到最大迭代次数；

• 在某一轮迭代中没有发生任何权重更新（即所以样本都分类正确）。

具体例子

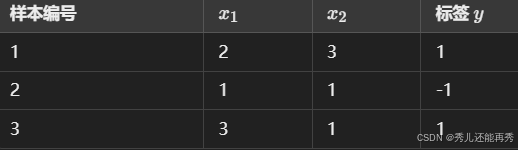
假设我们有以下一个简单的训练数据集。

初始化时设定权重 w1=0.1，w2=0.2，偏置 b=0，学习率 η=0.01。

第一轮迭代：

对于样本1，计算加权和：z=0.1×2+0.2×3+0=0.8。 激活函数输出 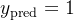，与真实标签一致，因此不更新权重。

对于样本2，计算加权和：z=0.1×1+0.2×1+0=0.3。激活函数输出 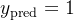，但真实标签是 -1，所以发生分类错误。更新权重和偏置：

对于样本3，计算加权和：z=0.08×3+0.18×1−0.02=0.4。激活函数输出 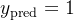，与真实标签一致，因此不更新权重。

第二轮迭代：

...

一直迭代。

直到所有样本分类正确或达到停止条件，得到了我们要的 w 和 b

#  若文章对大噶有帮助的话，点个赞支持一下叭！