机器学习基础--基于k-means实现鸢尾花聚类

k-mean 聚类算法的含义是根据给定的样本集合，按照样本之间的距离大小，将样本划分为K个簇，让簇内的点尽量紧密联系在一起，而簇间的距离尽可能大

鸢尾花数据集描述

1、包含3种类型数据集，共150条数据；2、包含4项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度

导入相关的包

import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans 
from sklearn import datasets

加载数据集

# 直接从sklearn中获取数据集
iris = datasets.load_iris()
X = iris.data
print(X.shape)

iris = datasets.load_iris()
这一行代码加载了鸢尾花（Iris）数据集。datasets.load_iris() 是 sklearn 库中的一个方法，它返回一个包含鸢尾花数据集的字典对象。该数据集包含了 150 个样本，分为 3 类，每一类有 50 个样本。每个样本有 4 个特征。

iris.data 是一个 NumPy 数组，包含了鸢尾花数据集中的所有特征。

定义K-mean类，并定义训练函数

def Model(n_clusters):
    estimator = KMeans(n_clusters=n_clusters)# 构造聚类器
    return estimator

def train(estimator):
    estimator.fit(X)  # 聚类

# 初始化实例，并开启训练拟合
estimator=Model(3)     
train(estimator)

n_clusters表示要聚类的数量，调用kmeans方法进行聚类分析

fit(X) 是训练模型的函数。这里，X 是输入数据，表示你希望进行聚类分析的数据。
fit(X) 会根据 X 中的数据进行训练，学习出数据的簇（clusters）。KMeans 算法会自动根据数据的结构将其划分成指定数量的簇（通过 n_clusters）

绘制图片

label_pred = estimator.labels_  # 获取聚类标签
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
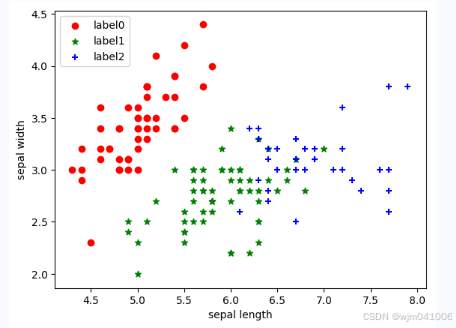
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()

上面就是借助已经封装号的方法来进行K-means聚类，那么下面介绍手动实现K-mean聚类

# 欧氏距离计算
def distEclud(x,y):
    return np.sqrt(np.sum((x-y)**2))  # 计算欧氏距离
 
# 为给定数据集构建一个包含K个随机质心centroids的集合
def randCent(dataSet,k):
    m,n = dataSet.shape #m=150,n=4
    centroids = np.zeros((k,n)) #初始化质心为0，其中K代表簇数，n代表特征数，均为4
    for i in range(k): # 执行四次
        index = int(np.random.uniform(0,m)) # 产生0到150的随机数（在数据集中随机挑一个向量做为质心的初值）
        centroids[i,:] = dataSet[index,:] #把对应行的四个维度传给质心的集合
    return centroids
 
# k均值聚类算法
def KMeans(dataSet,k):
    m = np.shape(dataSet)[0]  #行数150
    # 第一列存每个样本属于哪一簇(四个簇)
    # 第二列存每个样本的到簇的中心点的误差
    clusterAssment = np.mat(np.zeros((m,2)))# .mat()创建150*2的矩阵
    clusterChange = True
 
    # 1.初始化质心centroids
    centroids = randCent(dataSet,k)#4*4
    while clusterChange:
        # 样本所属簇不再更新时停止迭代
        clusterChange = False
 
        # 遍历所有的样本（行数150）
        for i in range(m):
            minDist = 100000.0
            minIndex = -1
 
            # 遍历所有的质心
            #2.找出最近的质心
            for j in range(k):
                # 计算该样本到4个质心的欧式距离，找到距离最近的那个质心minIndex
                distance = distEclud(centroids[j,:],dataSet[i,:])
                if distance < minDist:
                    minDist = distance
                    minIndex = j
            # 3.更新该行样本所属的簇
            if clusterAssment[i,0] != minIndex:
                clusterChange = True
                clusterAssment[i,:] = minIndex,minDist**2
        #4.更新质心
        for j in range(k):
            # np.nonzero(x)返回值不为零的元素的下标，它的返回值是一个长度为x.ndim(x的轴数)的元组
            # 元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。
            # 矩阵名.A 代表将 矩阵转化为array数组类型
            
            # 这里取矩阵clusterAssment所有行的第一列，转为一个array数组，与j（簇类标签值）比较，返回true or false
            # 通过np.nonzero产生一个array，其中是对应簇类所有的点的下标值（x个）
            # 再用这些下标值求出dataSet数据集中的对应行，保存为pointsInCluster（x*4）
            pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]]  # 获取对应簇类所有的点（x*4）
            centroids[j,:] = np.mean(pointsInCluster,axis=0)   # 求均值，产生新的质心
            # axis=0，那么输出是1行4列，求的是pointsInCluster每一列的平均值，即axis是几，那就表明哪一维度被压缩成1

机器学习基础--基于k-means实现鸢尾花聚类

悦读