手机查看图片不知道为什么不能显示,请在电脑上查看。
我们日常 喝的饮料 和 吃的药片 都是由一些 基本元素 调和而成的
比如:
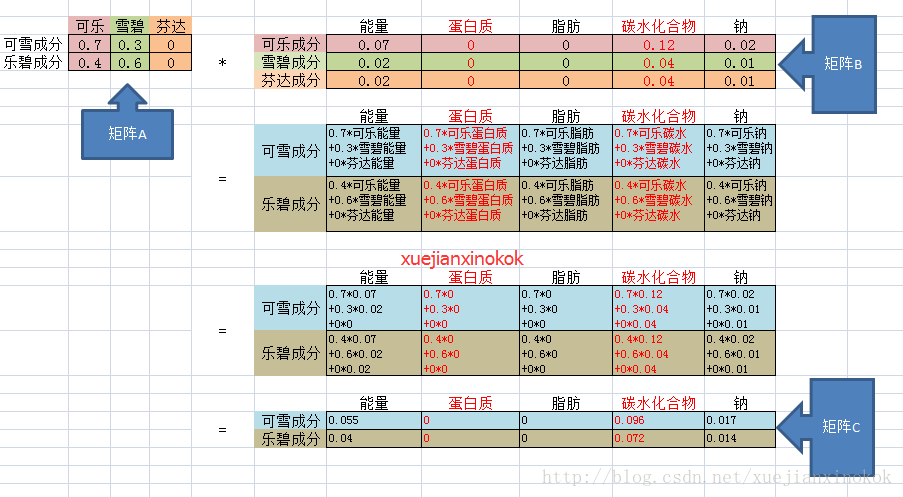
我们列出以下公式 B:
可乐=0.07* 能量+ 0*蛋白质+0*脂肪+0.12* 碳水化合物 +0.02* 钠
雪碧=0.02* 能量+ 0*蛋白质+0*脂肪+0.04* 碳水化合物 +0.01* 钠
芬达=0.02* 能量+ 0*蛋白质+0*脂肪+0.04* 碳水化合物 +0.01* 钠
如果 把可乐和 雪碧,芬达 看成3种 高级成分
我们就可以立刻发明多种新的饮料:比如 可雪,乐碧
这两种饮料的配料成分明细如下 公式A:
可雪=0.7 *可乐+0.3* 雪碧+0*芬达
乐碧=0.4 *可乐+0.6* 雪碧+0*芬达
我们可以这样理解:
现实中的 物品(可雪,乐碧) 都有 一组高级成分(可乐,雪碧,芬达)组成,
而这些高级成分又可以分级为 次级成分(能量,蛋白质,脂肪, 碳水化合物, 钠)
如果 我们想知道 可雪 的具体成分含量(能量,蛋白质,脂肪, 碳水化合物, 钠), 只需要将 A和B 进行矩阵乘法即可
结果应该是 2行 5列的矩阵C,C 表示了可雪 和 乐碧 的具体成分含量
计算过程如下:
假设现在 我们知道矩阵C 现在想把矩阵C 分解成矩阵A 和 B
这样的话 我们把 A 叫做 高阶特征权重矩阵,即 (可雪,乐碧) 由 高阶特征(可乐,雪碧,芬达)线性组合而成 ,
B 叫低阶特征权重矩阵 (可乐,雪碧,芬达) 由 (能量,蛋白质,脂肪, 碳水化合物, 钠)线性组合而成
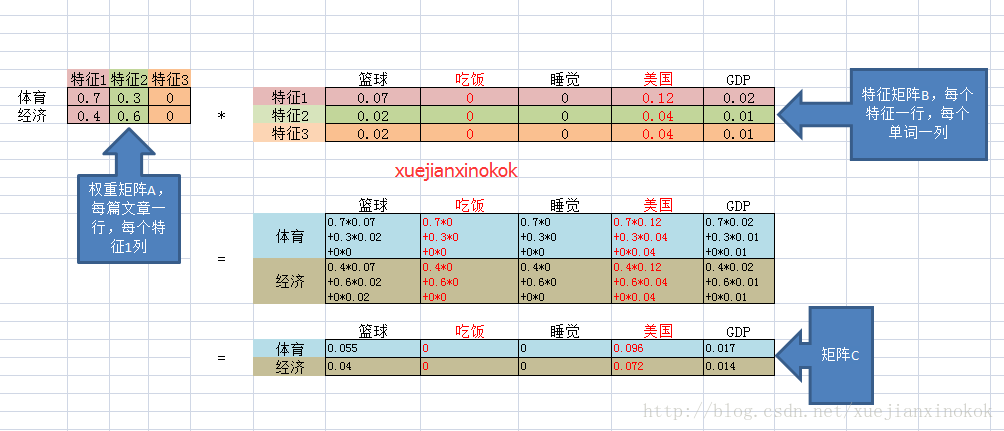
如果换成自然语言处理原理同上(例子有点不太适合,理解意思即可):
在自然语言处理和推荐系统中 我们一般能够直接得到矩阵 C ,C 是非常稀疏的,我们想把C 分解成 高阶特征的线性组合,这样便于分类和预测
这就是为什么要将大矩阵进行分解。
常见的分解方式 有PCA,SVD ,NMF矩阵分解。
参考文章:《数学之美 第二版》 第15章 矩阵运算和文本处理中的两个分类问题
《集体智慧编程》 第10章 寻找独立特征_NMF
《线性代数及其应用》