前言
本篇博客主要记录拓扑排序的实现。包括卡恩算法实现和dfs+深度搜索算法实现。其实这两个算法本质分别是广度优先搜索和深度优先搜索。
一、拓扑排序规则
首先知道入度和出度的概念,箭头指向本顶点,则本顶点的入度就+1,箭头指出。则出度+1。
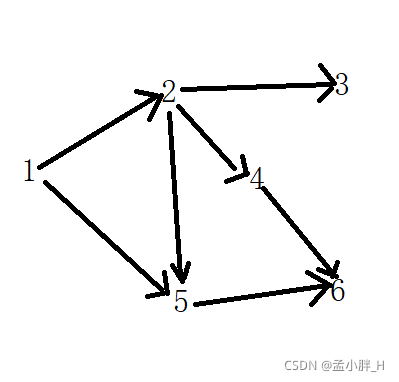
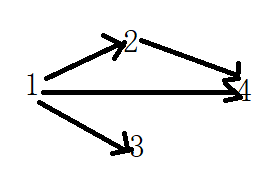
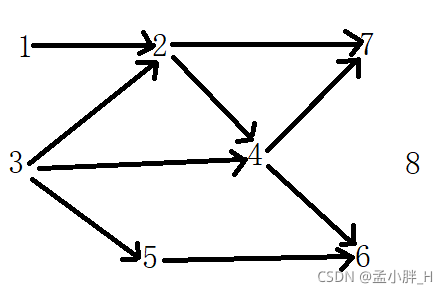
拓扑排序即把入度为0的结点一个一个找出来,看下例子就知道了:
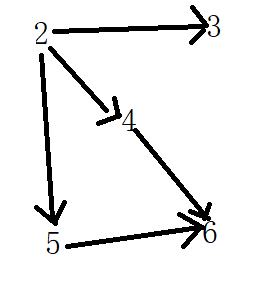
上图中1入度为0,所以1排在前面,此时拓扑排序为{1},将1指出去的箭头都擦去,将下面的继续进行排序:
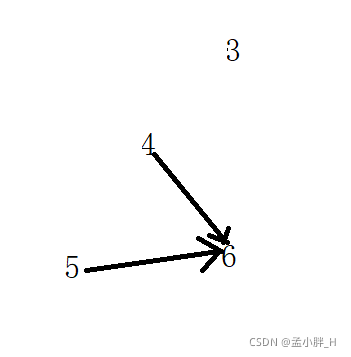
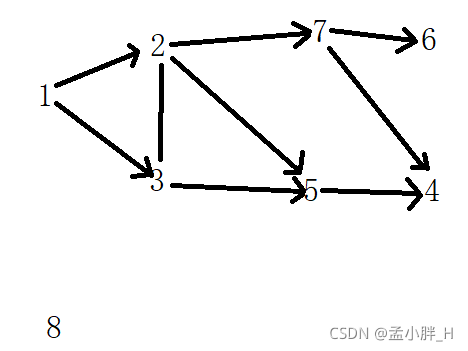
上图中2入度为0,所以2到拓扑排序中,此时拓扑排序为{1,2},将顶点2和从2指出去的箭头擦去,继续进行找入度为0的顶点:
如上图,此时入度为0的顶点有3,4,5三个顶点,所以这三个顶点谁在前面或者后面都行(这也说明了,拓扑排序结果不具有唯一性)。在这里我们按照3,4,5取,那么拓扑排序为{1,2,3,4,5},最后还剩一个6,入度0,将6放进去,拓扑排序为{1,2,3,4,5,6}。
拓扑排序需要注意几点:
(1)AOV网的顶点都是值唯一的,不存在说两个不同的顶点,但是这两个顶点都是A或者说都是1。
(2)拓扑排序的结果不具有唯一性,因为待排序的顶点中,可能同时有多个顶点入度为0。
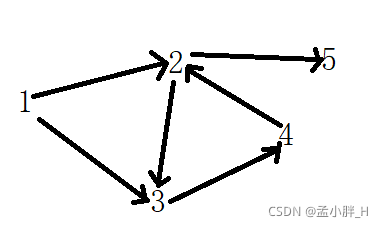
(3)AOV网中不允许存在环,即顺着箭头指向走,不可能再走回到原来的顶点,如下就是有环的(2->3->4->2):
有环的一定会造成死循环,无法进行拓扑排序。
二、卡恩算法实现
1.卡恩算法思想
卡恩算法的思想即将当前的入度为0的顶点取出来,将顶点及和从该顶点出发的箭头擦除,寻找剩下顶点中入度为0的顶点…直到顶点都完成拓扑排序。和上面拓扑排序归则中的思想一样。
2.代码实现
拓扑排序的代码中,有多个数组,比如存放原AOV网关系的二维数组vc{{1,2},{1,3},{1,4},{2,4}}就代表一个AOV网:
(1指向2,我们将2称为1的邻接顶点,1指向3,我们将3称为1的邻接顶点…)
会有一个二维数组neighbor存放每个顶点的邻接顶点,neighbor[1][0]=2表示1的一个邻接顶点是2;neighbor[1][1]=3表示1的一个邻接顶点是3…
另外会有一个一维数组iv存放每个顶点的入度,iv[1] == 0表示1的此时入度为0,iv[4] == 2表示顶点4的此时入度为2。
当我们将入度为0 的顶点1拿走时,会用neighbor查询1的邻接点,然后将1的邻接点的入度都-1,再判断这些邻接点的入度-1后是否为0,为0就把顶点拿走…
由于每个数组之间都有一定的联系,所以导致代码中的数组使用看着有点混乱,但是只要理清楚每个数组什么作用,就比较明了。
代码:
//拓扑排序,Kohn算法,有环返回空数组
vector<int> TuopuSort(vector<vector<int>>& vc, int numV)//numV是顶点的个数
{
vector<int>tar; //存放排序后的顶点
int numE = vc.size(); //numE是边个数
vector<int>iv(numV+1, 0);//iv[i] == j表示顶点i的入度为j
vector<vector<int>>neighbor(numV+1); //neighbor[i][j] == k表示顶点i邻接顶点是k
for (int i = 0; i < numE; i++) //统计每个结点的入度
{
neighbor[vc[i][0]].push_back(vc[i][1]);//记录顶点vc[i][0]的邻接顶点
iv[vc[i][1]]++; //记录顶点的入度
}
queue<int>qu; //记录入度为0的顶点
for (int i = 1; i < iv.size(); i++)//将入度为0的顶点入到队列中
{
if (iv[i] == 0)
{
qu.push(i);
}
}
while (!qu.empty())
{
int t = qu.front(); qu.pop();//取出队列中的一个顶点,队列中的顶点都是入度为0的顶点,注意这里一定要用队列,不能用栈
tar.push_back(t); //将入度为0的顶点加入到tar中
for (int i = 0; i < neighbor[t].size(); i++)
{
if (--iv[neighbor[t][i]] == 0) //将t的邻接顶点的入度-1,并判断这个邻接顶点入度-1后是否为0,入度为0就入到队列中
{
if (neighbor[t][i] != 0)//注意邻接点可能是0,0只是标记,不起作用,也不是顶点,所以要加判断
{
qu.push(neighbor[t][i]);
}
}
}
}
if (tar.size() == numV) //说明所有顶点都放到tar中了,说明都完成了排序
return tar;
else
return {};
}
//拓扑排序,两个顶点值不能重复,否则就认为是指同一个顶点,不允许有环,否则排序过后返回空,代表排序失败
int main()
{
//注意,顶点0不允许使用,顶点最少从1开始,0在拓扑排序中起标识作用
//出度和出度都为0的顶点x一开始用{x,0}表示,如下{8,0}表示8是孤立顶点,既没有入度也没有出度
vector<vector<int>>vc{ {8,0}, {1,2},{2,7},{7,6},{2,3} ,{2,5},{7,4},{1,3},{3,5}, {5,4} };
vector<int>tar = TuopuSort(vc, 8);//传入顶点数
for (auto& x : tar)
{
cout << x << " ";
}
cout << endl;
return 0;
}
运行结果:
三、dfs+深度优先
1.算法思想
主要用dfs和深度优先搜索结合,每次都沿着一条路径一直向下搜索,直到某个顶点的出度为0或被标记已经访问,就停止递归,往回走,在回来的路上记录拓扑排序,即后序遍历。(所以我们得到的拓扑排序是翻着的,反转一下就好了)
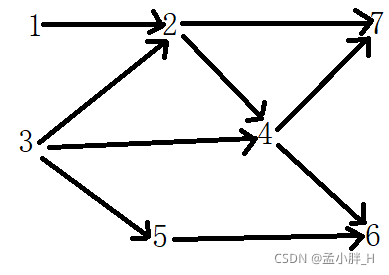
如下图:
从入度为0的顶点深度优先遍历:
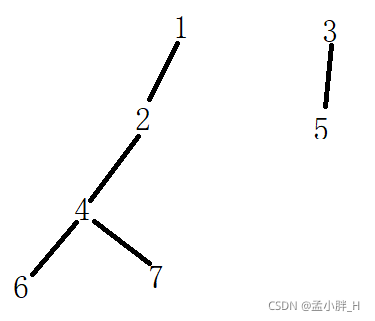
先从1深度优先遍历,再从3深度优先遍历(注意:遍历过的顶点会做标记,不会遍历第二次)
tar中的序列为{6,7,4,2,1,5,3},这个是深度优先遍历的结果,记录的是后序遍历,因为我们是一直向下递归,回退的时候,将结点值一个一个放入到tar中的(见代码实现部分)。反转即为我们要的拓扑排序序列。即拓扑排序序列{3,5,1,2,4,7,6}。
2.代码实现
本代码中和卡恩算法一样,需要用vc,neighbor,iv数组,除此之外,本算法还需要数组visit标识结点是否被访问过,visit[i]==true表明i结点被访问过了。
代码:
void dfs(vector<int>& tar, vector<bool>& visit, vector<vector<int>>& neighbor, int v)
{
for (int i = 0; i < neighbor[v].size(); i++)//从顶点i开始深度优先遍历
{
if (!visit[neighbor[v][i]])//说明邻接点没有被访问,从邻接顶点继续向下深度遍历
{
visit[neighbor[v][i]] = true;
dfs(tar, visit, neighbor, neighbor[v][i]);
}
}
if (v != 0)//防止0入拓扑排序(0是标识,方便操作,0不是顶点)
{
tar.push_back(v);//从后向前记录拓扑序列(得到的是反的拓扑序列)
}
}
vector<int> TuopuSort(vector<vector<int>>& vc, int numV)//numV是顶点的个数
{
vector<int>tar; //存放排序后的顶点
int numE = vc.size(); //numE是边个数
vector<int>iv(numV + 1, 0);//iv[i] == j表示顶点i的入度为j
vector<vector<int>>neighbor(numV + 1); //neighbor[i][j] == k表示顶点i邻接顶点是k
vector<bool> visit(numV + 1, 0);
for (int i = 0; i < numE; i++) //统计每个结点的入度
{
neighbor[vc[i][0]].push_back(vc[i][1]);//记录顶点vc[i][0]的邻接顶点
iv[vc[i][1]]++; //记录顶点的入度
}
for (int i = 1; i <= numV; i++)//遍历顶点
{
if (iv[i] == 0 && !visit[i])//从入度为0的顶点开始深度优先遍历
{
visit[i] = true;//遍历过的顶点标志为true
dfs(tar, visit, neighbor, i);
}
}
reverse(tar.begin(), tar.end());
return tar;
}
//拓扑排序,两个顶点值不能重复,否则就认为是指同一个顶点,不允许有环,否则排序过后返回空,代表排序失败
int main()
{
//注意,顶点0不允许使用,顶点最少从1开始
//出度和出度都为0的顶点x一开始用{x,0}表示,如下{8,0}表示8是孤立顶点,既没有入度也没有出度
vector<vector<int>>vc{ {1,2},{2,4},{2,7},{3,2},{3,4},{3,5},{4,6},{4,7},{5,6},{8,0} };
vector<int>tar = TuopuSort(vc, 8);//传入顶点数
for (auto& x : tar)
{
cout << x << " ";
}
cout << endl;
return 0;
}
运行结果:
总结
卡恩算法本质就是广度优先遍历,比较直接,每次都将产生的入度为0的顶点加到拓扑序列中,直到顶点都被加入进去(除非有环,会导致顶点没有全被加到拓扑序列中,而且也没有入度为0的顶点了,这种情况视为排序失败)。
dfs+深度优先遍历,主要利用了递归的思想,后序遍历将顶点加入到拓扑序列中,dfs思想保证了每个顶点只被遍历一次。得到的拓扑序列反转即为我们需要的拓扑排序后的结果。这算法没有卡恩算法直接,蒜贩思想也没有卡恩算法的思想更容易理解。