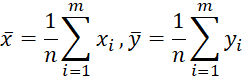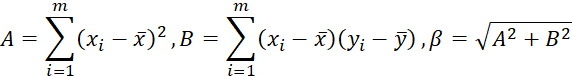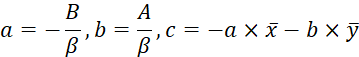C++拟合直线与求拟合误差实验

设计思路

一个平面点由两个坐标(x,y)确定，请编写一个表示平面点的类Point。要求：

在默认构造函数中初始化类对象为原点（0，0）；
添加一个带参数的构造函数，传入两个坐标值。
添加拷贝构造函数。
添加赋值操作函数operator=。
为类的两个成员添加getter函数和setter函数，getter函数为const函数；
平面直线的方程为ax+by+c=0 ，请设计一个类Line，表示一条平面直线。要求：
在默认构造函数中初始化直线为x轴。
添加一个带参数的构造函数，传入直线方程的三个系数。
添加拷贝构造函数。
添加赋值操作函数operator=。
添加一个函数，获取直线的方向。
添加一个函数，获取该直线的三个参数。
添加一个函数，计算点到直线的距离，函数的参数是第一题的Point类对象。
添加一个函数，判断一个点是否在这条直线上，函数的参数是第一题的Point类对象。提示：由于存在计算误差，当点到直线的距离小于一个很小的阈值时，可以认为点在直线上。
编写一个函数，用于生成一组随机点Pi=xi,yi,i=1…m ，这些随机点都是某一条直线l:ax+by+c=0上的点，但是受到很小的噪声污染，即， ,其中ηi 是一个很小的噪声，服从0均值高斯分布（使用std::normal_distrubtion生成满足高斯分布的随机数来模拟这个噪声，参考：http://www.cplusplus.com/reference/random/normal_distribution/）。函数的输入为一个Line对象，样本点数目，输出为随机点数组。提示：使用vector<Point>传回生成的随机点对象数组。
编写一个函数FitLine，该函数传入一组随机点，返回一条直线。该直线是采用最小二乘法，用传入的随机点拟合的直线。
编写一个函数CalcDistance，计算一组点到一条直线的平均距离。
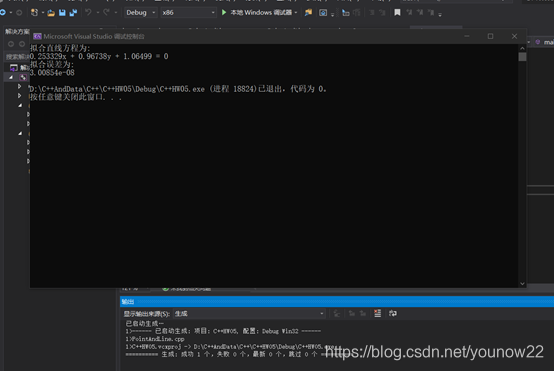
在main函数中，生成一个Line对象L0，并调用上述函数生成随机点集，然后调用你的FitLine函数拟合出直线L1。并用CalcDistance函数计算你所得到的直线L1与样本点集之间的拟合误差（即平均距离）。在main函数中，输出真实直线L0的方程，拟合直线L1的方程，以及拟合误差。

本实验需要了解的算法知识如下：

源码

Main.cpp

//Main.cpp
#include "leastSquare.h"
#include <iostream>
#include<ctime>
#include<random>
using namespace std;
using namespace leastSquare;
using namespace PointAndLine;
int main(int argc, char* argv[])
{
	srand(time(0));
	
	float ran1 = 0 + 1.0 * (rand() % RAND_MAX) / RAND_MAX * (1 - 0);
	float ran2 = 0 + 1.0 * (rand() % RAND_MAX) / RAND_MAX * (1 - 0);
	float ran3 = 0 + 1.0 * (rand() % RAND_MAX) / RAND_MAX * (1 - 0);
	
	PointAndLine::Line L0(ran1,ran2,ran3), L1;
	
	vector<Point> ptr = GenRanPoint(L0, 100);
	L1 = FitLine(ptr);
	float dis = CalcDistance(ptr, L1);

	float a, b, c;
	L1.getter(a, b, c);
	cout << "拟合直线方程为:" << endl;
	cout << a << "x + " << b << "y + " << c <<" = 0" << endl;
	cout << "拟合误差为:" << endl;
	cout << dis << endl;
	return 0;

其他文件和函数

leastSquare.h

//leastSquare.h
#ifndef _LEASQU_H_
#define _LEASQU_H_
#include<iostream>
#include <vector>
#include"PointAndLine.h"
using namespace PointAndLine;
using namespace std;
namespace leastSquare
{
	vector<Point> GenRanPoint(Line l, int num);
	Line FitLine(vector<Point> ptr);
	float CalcDistance(vector<Point> ptr, Line l);
}
#endif

leastSquare.cpp

//leastSquare.cpp
#include"leastSquare.h"
#include<cmath>
using namespace leastSquare;
float gaussrand()
{
	static float V1, V2, S;
	static int phase = 0;
	float X;

	if (phase == 0) {
		do {
			float U1 = (float)rand() / RAND_MAX;
			float U2 = (float)rand() / RAND_MAX;

			V1 = 2 * U1 - 1;
			V2 = 2 * U2 - 1;
			S = V1 * V1 + V2 * V2;
		} while (S >= 1 || S == 0);

		X = V1 * sqrt(-2 * log(S) / S);
	}
	else
		X = V2 * sqrt(-2 * log(S) / S);

	phase = 1 - phase;

	return X;
}
vector<Point> leastSquare::GenRanPoint(Line l, int num)
{
	float a, b, c;
	l.getter(a, b, c);
	float theta = gaussrand();
	vector<Point> p;
	for(int x = 1;x<num+1;x++)
	{
		x = static_cast<float>(x);
		float y = static_cast<float>((-a / b) * x - (c / b) + theta);
		Point index(x, y);
		p.push_back(index);
	}
	return p;
}
Line leastSquare::FitLine(vector<Point> ptr)
{
	float x = 0, y = 0, A = 0, B = 0, beta = 0;
	for(unsigned int i=0;i<ptr.size();i++)
	{
		x += ptr[i].getter_x();
		y += ptr[i].getter_y();
	}
	x = x / ptr.size();
	y = y / ptr.size();
	for (unsigned int i = 0; i < ptr.size(); i++)
	{
		A += pow(x - ptr[i].getter_x(), 2);
		B += (y - ptr[i].getter_y())*(x - ptr[i].getter_x());
	}
	beta = static_cast<float>(sqrt(pow(A, 2) + pow(B, 2)));
	const float a =static_cast<float>( -B / beta);
	const float b = static_cast<float>(A / beta);
	const float c = -a * x - b * y;
	Line line(a,b,c);
	return line;
}
float leastSquare::CalcDistance(vector<Point> ptr, Line l)
{
	float distance  = 0;
	for(int i = 0;i < ptr.size();i++)
	{
		distance += l.calcDistance(ptr[i]);
	}
	distance = distance / ptr.size();
	return distance;
}

PointAndLine.h

#ifndef __PAL_CPP_
#define _PAL_CPP_
#include <cstdlib>
#include <cstddef>
namespace PointAndLine
{
	class Point
	{
	private:
		float x, y;
		friend class Line;
	public:
		Point() :x(0), y(0) {}
		Point(float _x, float _y);
		Point(const Point& p);
		Point& operator=(const Point& p);
		float getter_x()const;
		float getter_y()const;
		void setter(float _x, float _y);
	};

	class Line
	{
	private:
		float a, b, c;
	public:
		Line():a(0),b(1),c(0){}
		Line(float _a,float _b,float _c);
		Line(const Line& l);
		Line& operator=(const Line& l);
		void getter(float& _a, float& _b,float& _c)const;
		float calcDistance(Point p);
		bool point_In_line(Point p);
	};
}
#endif

PointAndLine.cpp

//PointAndLine.cpp
#include"PointAndLine.h"
#include<iostream>
#include<cmath>
using namespace std;
using namespace PointAndLine;
Point::Point(float _x,float _y)
{
	this->x = _x;
	this->y = _y;
}
Point::Point(const Point &p)
{
	x = p.x;
	y = p.y;
}
Point& Point::operator=(const Point& p)
{
	if(this==NULL)
	{
		x = p.x;
		y = p.y;
	}
	return *this;
}
float Point::getter_x() const
{
	return x;
}
float Point::getter_y() const
{
	return y;
}
void Point::setter(float _x,float _y)
{
	x = _x;
	y = _y;
}
Line::Line(float _a, float _b, float _c)
{
	a = _a;
	b = _b;
	c = _c;
}
Line::Line(const Line& l)
{
	a = l.a;
	b = l.b;
	c = l.c;
}
Line& Line::operator=(const Line& l)
{
	if(this!=NULL)
	{
		a = l.a;
		b = l.b;
		c = l.c;
	}
	return *this;
}
void Line::getter(float& _a, float& _b, float& _c)const
{
	_a = this->a;
	_b = this->b;
	_c = this->c;
}
float Line::calcDistance(Point p)
{
	return static_cast<float>(abs(a * p.x + b * p.y + c) / sqrt(pow(p.x, 2)+pow(p.y, 2)));
}
bool Line::point_In_line(Point p)
{
	if(a*p.x+b*p.y+c<static_cast<float>(1e-1))
	{
		return true;
	}
	return false;
}

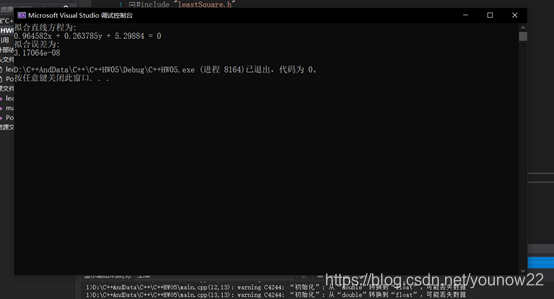
运行结果

5个拟合点：

100个拟合点：

C++拟合直线与求拟合误差实验

设计思路

源码

Main.cpp

leastSquare.h

leastSquare.cpp

PointAndLine.h

PointAndLine.cpp

运行结果

悦读