计算机的错误计算（九）

摘要计算机的错误计算（八）探讨了 Sigmoid 函数的导数的计算误差。本节讨论 Tanh函数（双曲正切函数）的导数的计算误差。

Tanh函数，也称为双曲正切函数，是一种在神经网络中常用的激活函数。它的数学表达式为：

$\textup{tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ .

Tanh函数的导数为：

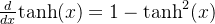
$\frac{d}{dx}\textup{tanh}(x)=1-\textup{tanh}^2(x)$ .

例1. 不妨令 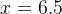x=6.5 ，并用下列C代码计算：

$double \,\,\,x,y1,y2,z1,z2,result;\\ x=6.5;\\ y1=exp(x);\\ y2=1/y1;\\ z1=(y1-y2)/(y1+y2);\\ z2=z1*z1;\\ result=1-z2;\\printf(" \%.30f",result);$

则在 Visual Studio 2010 环境下，含有17位有效数字的输出结果为：0.90412767556058427e-5；而含有17位正确有效数字的结果为 0.90412767553505711e-5. 这样，计算机的输出中有 7 位错误数字。

即使只考虑前 15 或 16 位数字，错误数字也有五六位。

若在 Python 中使用 numpy 库中函数计算：

print("Result:", 1-np.tanh(6.5)**2)

则输出为 9.041276755383798e-06，同样有 5 位错误数字。

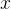
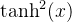
当的值越大， $\textup{tanh}^2(x)$ 越接近 1，这时，误差越大。

对这个误差，大家怎么看？大语言模型的幻觉（即一本正经的胡说八道）怎么来的？这也许是原因之一。