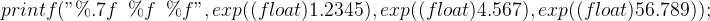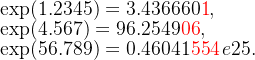计算机的错误计算（二十八）

摘要计算机的错误计算（七）阐述了：exp(x) 函数中有约 x 的整数位数位错误数字。由（二十七）知，其原因是 exp(x)的错数为 x 的整数位数。本节将通过几个实例，帮助大家进一步体验和加深理解。

不妨随机举几个案例：1.2345，4.567，56.789，87.654，123.45，700.123.

首先，若保留 20位有效数字，则正确结果为（由 ISReal 软件提供）

$\exp(1.2345)=0.34366597611704631832\,e1,\\ \exp(4.567)=0.96254911457897243606\,e2,\\ \exp(56.789)=0.46041486070104653690\,e25,\\ \exp(87.654)=0.11685532745660744672\,e39,\\ \exp(123.45)=0.41082209310966896424\,e54,\\ \exp(700.123)=0.11469792299253778723\,e305.$

然后，我们在不同的环境下查看它们的结果。

第一步，在Visual Studio 2010 的单精度下计算前面 3个数的exp(x)的函数值（后面 3 个超出单精度的计算范围）：

$printf("\%.7f\,\,\, \%f\,\,\, \%f",exp((float)1.2345),exp((float)4.567),exp((float)56.789));$

则保留 8位数字的结果分别为

$\exp(1.2345)=3.436660\textcolor{red}{1},\\ \exp(4.567)=96.2549\textcolor{red}{06},\\ \exp(56.789)=0.46041\textcolor{red}{554}\,e25.$

上面红颜色的数字是错误数字。所以，3个值的错误数字个数分别为 1位、2位、3位。

第二步，在Excel 的单元格中计算，则16位的结果为

$\exp(1.2345)=3.43665976117046\textcolor{red}{0},\\ \exp(4.567)=96.254911457897\textcolor{red}{30},\\ \exp(56.789)=0.46041486070104\textcolor{red}{70}\,e\,25,\\ \exp(87.654)=0.116855327456607\textcolor{red}{0}\,e\,39,\\ \exp(123.45)=0.4108220931096\textcolor{red}{700}\,e\,54,\\ \exp(700.123)=0.1146979229925\textcolor{red}{430}\,e\,305.$

同样，上面红颜色的数字是错误数字。因此，6个值的错误数字个数分别为 1位、2位、2位、1位、3位、3位。

那么如何获得准确值呢？不妨参考计算机的错误计算（二十三）。

计算机的错误计算（二十八）

悦读