成长路上不孤单😊😊😊😊😊😊
【😊///计算机爱好者😊///持续分享所学😊///如有需要欢迎收藏转发///😊】
今日分享关于C++中常用的排序方法之3——插入排序的相关内容!
关于【C++中常用的排序方法之3——插入排序】
目录:
- 一、插入排序的定义
- 二、插入排序的的思路及具体步骤
- 三、插入排序的的算法性能
- 四、 插入排序的适用场景
- 五、 插入排序的的特点
- 六、 插入排序的的优点
- 七、插入排序的的缺点
插入排序(Insertion sort)
一、插入排序的定义
选插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 [1]。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动 。
二、插入排序的思路及具体步骤
1、思路
插入排序的工作方式像许多人排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面向下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的,原来这些牌是桌子上牌堆中顶部的牌 。
插入排序是指在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
2、具体步骤
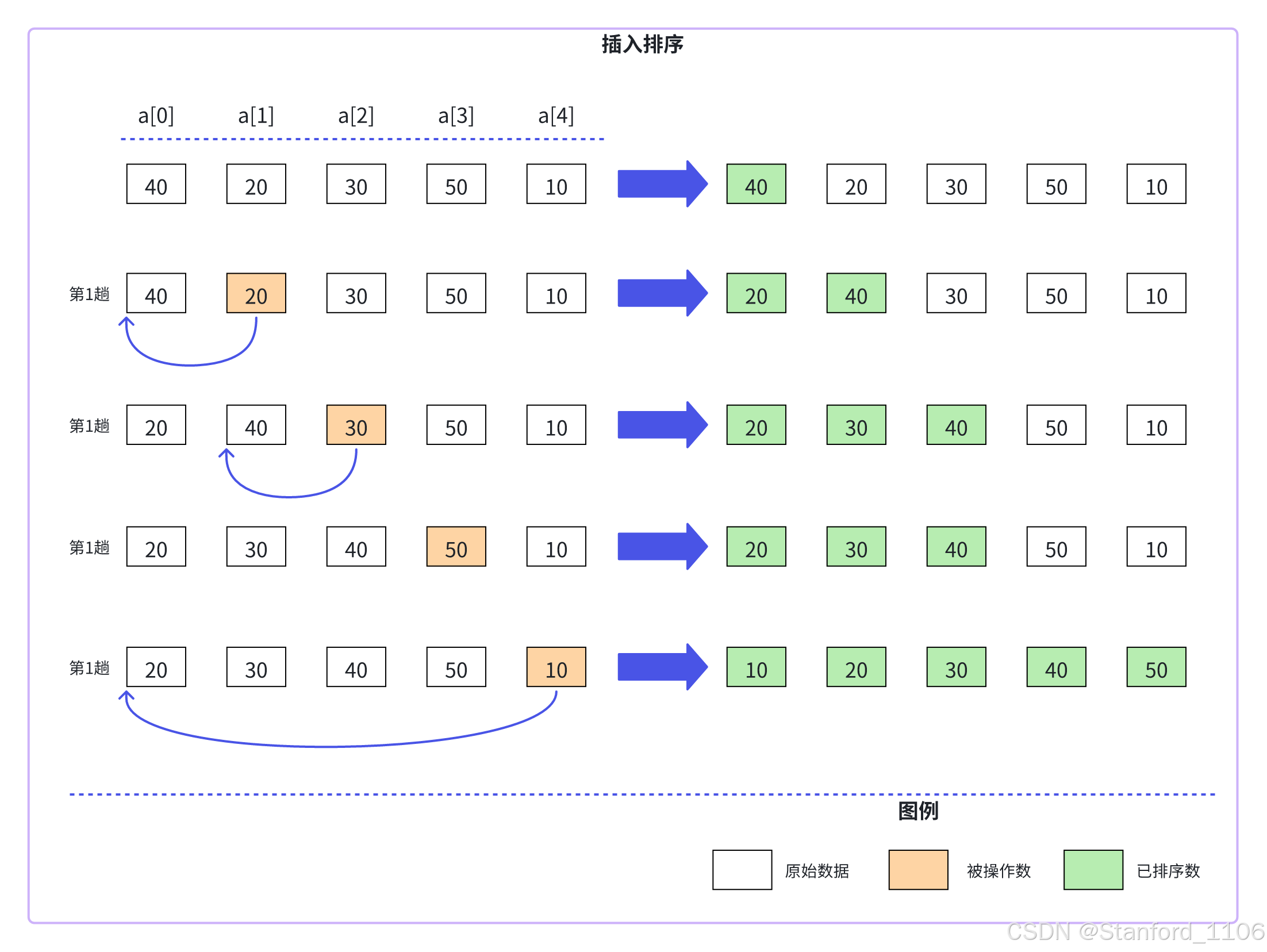
三、插入排序的算法性能
1、时间复杂度
插入排序的时间复杂度分为三种情况:
最好情况:当输入数组已经是有序的,每次插入操作只需要进行一次比较,时间复杂度为O(n)。
最坏情况:当输入数组是逆序的,每次插入操作需要进行n-1次比较和移动,时间复杂度为O(n^2)。
平均情况:当输入数组是随机排列的,时间复杂度大约为O(n^2)。
2、空间复杂度
插入排序的空间复杂度为O(1),因为它只需要一个很小的常数空间来存储变量。
稳定性:
插入排序是一种稳定的排序算法。稳定的排序算法能够保证相等元素的相对顺序不变。在插入排序中,相同元素的相对位置不会发生变化。
四、插入排序的适用场景
插入排序适用于小规模数据或基本有序的数据集。当数据接近有序时,插入排序的效率较高,因为它可以减少比较和移动的次数。
五、插入排序的特点
插入排序是一种简单的排序算法,其特点主要包括以下几个方面:
时间复杂度:插入排序的时间复杂度为O(n^2),在最坏的情况下(即初始序列为逆序),需要进行n*(n-1)/2次比较。然而,在最好的情况下(即初始序列已经有序),只需进行n-1次比较。
空间复杂度:插入排序是一种原地排序算法,其空间复杂度为O(1),因为它只需要常数级别的额外空间。
稳定性:插入排序是一种稳定的排序算法,即相等的元素在排序后保持原有的相对顺序。
适用场景:插入排序适用于数据量较小的情况,或者当数据几乎已经有序时,其效率较高。然而,对于大规模数据集,插入排序的性能较差。
算法思想:插入排序的基本思想是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增加1的有序表。具体过程是从数组的第二个元素开始,依次将其与前面的元素进行比较,找到合适的插入位置并插入。
性能分析:插入排序的性能主要取决于数据的初始顺序。当数据几乎有序时,插入排序的效率较高;反之,当数据完全无序时,其性能较差。
六、插入排序的优点
插入排序的优点主要包括以下几个方面:
实现简单,易于理解和编写:插入排序的算法逻辑非常直观,容易理解和实现,适合初学者学习和使用。
稳定性:插入排序是一种稳定的排序算法。这意味着在排序过程中,如果两个相等的元素在原序列中的顺序被保持,则排序结果是稳定的。例如,对于序列2, 3, 3, 4, 8, 9,排序后仍然是2, 3, 3, 4, 8, 9,保持了相等元素的原有顺序。
适用于小规模序列或基本有序的序列:插入排序在小规模数据或数据基本有序的情况下表现较好,因为它可以充分利用已排序的部分,减少比较和移动的次数。
原地排序:插入排序的空间复杂度为O(1),即它是一种原地排序算法,不需要额外的存储空间。
较好的最坏情况性能:尽管插入排序的最坏时间复杂度为O(n^2),但在某些情况下,如数据基本有序时,其性能可以接近O(n)。
七、插入排序的缺点
插入排序的主要缺点包括以下几个方面:
时间复杂度较高:插入排序的时间复杂度在最坏的情况下是O(n^2),其中n是待排序元素的数量。这意味着当数据量较大时,插入排序的效率会显著下降,不适合处理大规模数据集。
不适用于部分有序的数据:虽然插入排序在数据部分有序的情况下表现较好,但如果数据已经接近排序状态,其他排序算法(如归并排序或快速排序)通常会更高效。
不稳定:插入排序是一种不稳定的排序算法,相同的元素在排序后可能会改变它们原有的顺序。这意味着如果输入数组中有重复的元素,排序后这些元素的相对顺序可能会发生变化。
不适合实时应用:由于插入排序的时间复杂度较高,它不适合需要快速响应的应用场景,如实时数据处理系统。

