描述
有一个由按钮组成的矩阵,其中每行有6个按钮,共5行。每个按钮的位置上有一盏灯。当按下一个按钮后,该按钮以及周围位置(上边、下边、左边、右边)的灯都会改变一次。即,如果灯原来是点亮的,就会被熄灭;如果灯原来是熄灭的,则会被点亮。在矩阵角上的按钮改变3盏灯的状态;在矩阵边上的按钮改变4盏灯的状态;其他的按钮改变5盏灯的状态。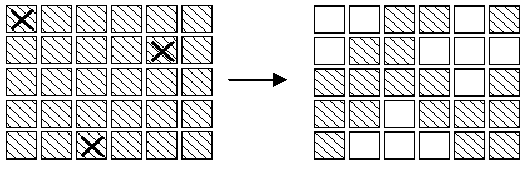
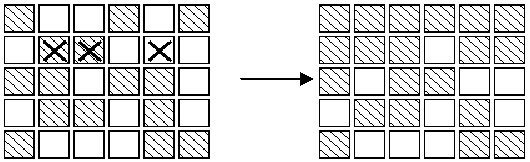
输入
5行组成,每一行包括6个数字(0或1)。相邻两个数字之间用单个空格隔开。0表示灯的初始状态是熄灭的,1表示灯的初始状态是点亮的。输出
5行组成,每一行包括6个数字(0或1)。相邻两个数字之间用单个空格隔开。其中的1表示需要把对应的按钮按下,0则表示不需要按对应的按钮。
如果直接枚举,每个灯有0、1两种状态,共30盏灯,就有2的30次方=1073741824种情况,肯定超时了。根据题意,我们可以采取部分枚举的方式,只枚举第一行或者第一列的状态。例如,当第一行的状态确定后,第二行只需扫描第一行的状态,如果发现第一行的某盏灯是亮的,就按下对应位置的按钮(同一列)熄灭这盏灯即可,第三行扫描第二行,第四行扫描第三行,第五行扫描第四行,最后,检测第五行灯的状态,如果全部都熄灭,即为所求解,如果仍有灯亮,则返回继续操作。
部分枚举,只枚举第一行,则只有2的6次方=64种情况,很显然不会超时。我们可以用二进制的方式来模拟这64种情况,从000000-111111。
#include <bits/stdc++.h>
using namespace std;
int a[10][10],b[10][10],c[10][10]; //数组a接收输入,记录灯的原始状态;数组b记录按钮的操作情况;数组c是a的备份,因为
void op(int x,int y){ //在一次操作中,a的值会发生改变,当不满足条件返回时,要将a回到原始状态
a[x][y]=!a[x][y];
a[x+1][y]=!a[x+1][y],a[x-1][y]=!a[x-1][y];
a[x][y+1]=!a[x][y+1],a[x][y-1]=!a[x][y-1];
}
bool check(){
for(int i=1;i<=6;i++)
if(a[5][i]==1)return false;
return true;
}
bool solve(){
for(int i=1;i<=6;i++) //根据第一行的状态,进行按钮操作
if(b[1][i]==1)op(1,i);
for(int i=2;i<=5;i++)
for(int j=1;j<=6;j++)
if(a[i-1][j]==1){ //根据前一行的状态,依次改变2、3、4、5行的状态
op(i,j);
b[i][j]=1;
}else b[i][j]=0;
if(check()){
for(int i=1;i<=5;i++,cout<<endl)
for(int j=1;j<=6;j++)
printf("%d ",b[i][j]);
return true;
}else{
for(int i=1;i<=5;i++)
for(int j=1;j<=6;j++)
a[i][j]=c[i][j];
return false;
}
}
int main(){
int t;
for(int i=1;i<=5;i++)
for(int j=1;j<=6;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=5;i++)
for(int j=1;j<=6;j++)
c[i][j]=a[i][j];
while(!solve()){ //枚举第一行的64种情况,从000000到111111,逢2进1
b[1][1]++;
t=1;
while(b[1][t]>1){
b[1][t]=0;
t++;
b[1][t]++;
}
}
return 0;
}