IK学习笔记（2）——TwoBones IK

几何法

Two Bones IK（二维情况）

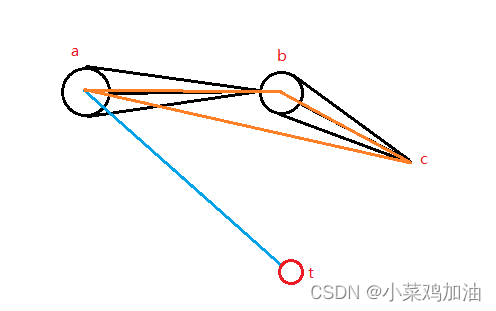
确定target的可达范围

在这里插入图片描述

首先根据ab和bc的长度确定target的可达范围

其中，at最长可以为ab + bc

最短需要简单分类讨论下，当ab > bc的时候，最短为ab - bc；当ab = bc的时候，最短为0；当ab < bc的时候，最短为bc - ab

因此，最短的情况综合起来是abs(ab - bc)

∴|at|∈[abs(ab - bc)，ab + bc]

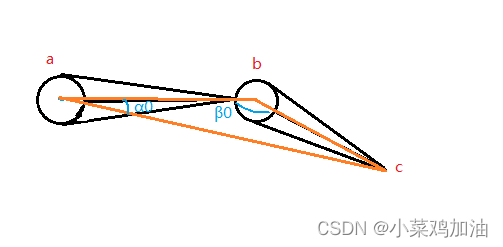
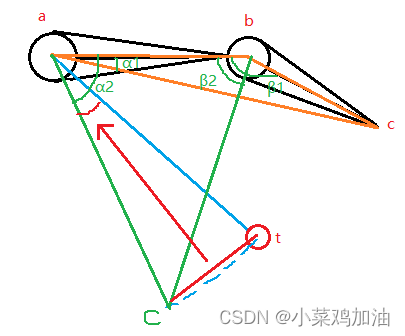
利用点积计算初始状态的夹角

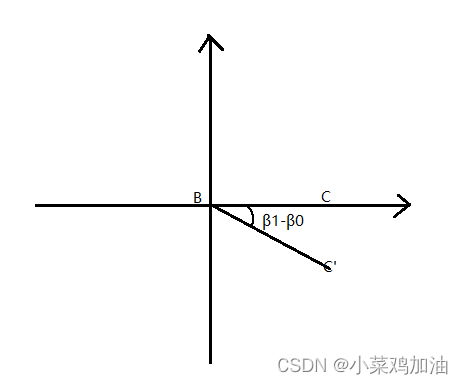
在这里插入图片描述

其中∠α $_{0}$ = $acos(\tfrac{AC·AB}{|AC||AB|})$

其中∠β $_{0}$ = $acos(\tfrac{BA·BC}{|BA||BC|})$

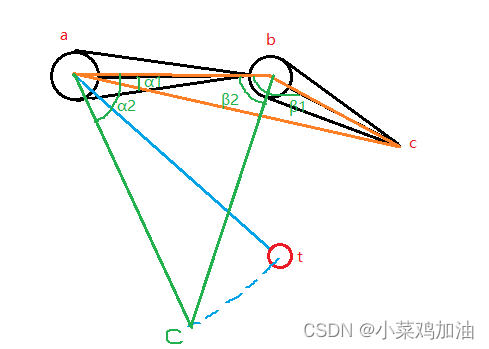
计算当|at| = |ac| 时的∠α ${_1}$ 和∠β ${_1}$

这里要把a看成圆点，然后利用|at| = |ac|这个条件使用余弦定理去计算

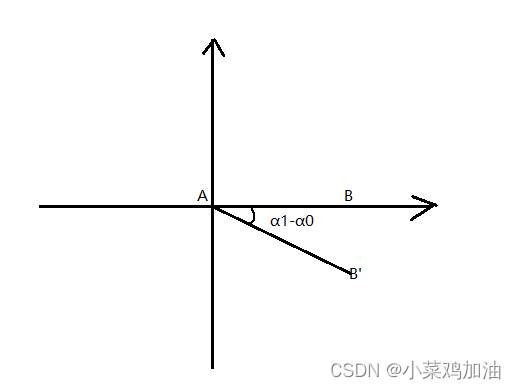
在这里插入图片描述

其中∠α $_{1}$ = $acos(\tfrac{bc^2-ab^2-at^2}{-2|ab||at|})$

其中∠β $_1$ = $acos(\tfrac{at^2-ab^2-bc^2}{-2|ab||bc|})$

在各自的local空间旋转

我们计算的时候使用的是世界空间坐标系，在这里旋转角度的时候使用local坐标系进行旋转，这样最终更新世界矩阵的时候的得到的是旋转后的结果

在这里插入图片描述

在a点旋转一个角度，让c点和t点重合

在这里插入图片描述

∠tac= $acos(\tfrac{at·ac}{|at||ac|})$

Two Bones IK（三维情况）

三维情况和二维情况的不同在于旋转的方向需要使用到向量的叉积得到法线，再利用正交化后的法线进行角度旋转

代码实现参考：https://zhuanlan.zhihu.com/p/447895503

void TwoBonesIK(const Vector3& target_pos)
{
	assert(m_bones_chain.size() >= 3);
	float eps = 0.01;

	Vector3 a = m_bones_chain[1].position - m_bones_chain[0].position; // AB 向量
	Vector3 inv_a = m_bones_chain[0].position - m_bones_chain[1].position; // BA向量
	float lab = a.Length();

	Vector3 b = m_bones_chain[2].position - m_bones_chain[1].position; // BC 向量
	float lbc = b.Length();

	Vector3 c = m_bones_chain[2].position - m_bones_chain[0].position; // AC 向量

	Vector3 tar_dir = target_pos - m_bones_chain[0].position; // AT向量
	float lat = tar_dir.Length();
	// 第一步：限制
	//if (lat <= fabs(lab - lbc)) lat = fabs(lab - lbc);
	if (lat <= eps) lat = eps;
	if (lat >= lab + lbc - eps) lat = lab + lbc - eps;

	// 第二步：计算初始状态的角度
	a.Normalize();
	inv_a.Normalize();
	b.Normalize();
	c.Normalize();
	tar_dir.Normalize();

	float temp1 = (c.Dot(a) / (c.Length() * a.Length()) );
	if (temp1 <= -1.0f) temp1 = -1.0f;
	if (temp1 >= 1.0f) temp1 = 1.0f;
	float ac_ab_0 = acos(temp1);
	float temp2 = (inv_a.Dot(b)/(inv_a.Length() * b.Length()));
	if (temp2 <= -1.0f) temp2 = -1.0f;
	if (temp2 >= 1.0f) temp2 = 1.0f;
	float ba_bc_0 = acos(temp2);
	// 最后一步旋转要用
	float temp3 = (c.Dot(tar_dir) / (c.Length() * tar_dir.Length()));
	if (temp3 <= -1.0f) temp3 = -1.0f;
	if (temp3 >= 1.0f) temp3 = 1.0f;
	float ac_at_0 = acos(temp3);
	// 第三步：计算|at|=|ac|时的新角度(余弦定理)
	float temp4 = (lbc * lbc - lab * lab - lat * lat) / (-2 * lab * lat);
	if (temp4 <= -1.0f) temp4 = -1.0f;
	if (temp4 >= 1.0f) temp4 = 1.0f;
	float ac_ab_1 = acos(temp4);
	float temp5 = (lat * lat - lab * lab - lbc * lbc) / (-2 * lab * lbc);
	if (temp5 <= -1.0f) temp5 = -1.0f;
	if (temp5 >= 1.0f) temp5 = 1.0f;
	float ba_bc_1 = acos(temp5);

	// 第四步：在各自的local空间进行旋转，得到|ac|=|at|
	Vector3 axis0;
	if (openAxis)
	{
		Vector3 d;
		Rotation temp = m_bones_chain[1].rotation;
		temp.RotateVector(d, math3d::Vector3(0,0,1));
		c.Cross(d, axis0);
	}
	else c.Cross(a, axis0);
	axis0.Normalize();

	Vector3 axis1; // 最后一步旋转使用
	c.Cross(tar_dir, axis1);
	axis1.Normalize();
		// 通过角度求四元数
	Rotation copy0 = m_bones_chain[0].rotation;
	copy0.Normalize();
	Rotation a_gr = copy0.Inverse(); // 世界坐标旋转 into local space
	Vector3 vec_dest0;
	a_gr.RotateVector(vec_dest0, axis0);
	Rotation r0(vec_dest0, ac_ab_1 - ac_ab_0);
		// 通过角度求四元数
	Rotation copy1 = m_bones_chain[0].rotation;
	copy1.Normalize();
	Rotation b_gr = copy1.Inverse(); // 世界坐标旋转 into local space
	Vector3 vec_dest1;
	b_gr.RotateVector(vec_dest1, axis0);
	Rotation r1(vec_dest1, ba_bc_1 - ba_bc_0);

	// 第五步：最后在a点旋转一个角度，让c与t重合
	Vector3 vec_dest2;
	a_gr.RotateVector(vec_dest2, axis1);
	Rotation r2(vec_dest2, ac_at_0);


	auto& a_lr = m_bones_chain[0].local_rot;
	a_lr *= (r0 * r2);

	auto& b_lr = m_bones_chain[1].local_rot;
	b_lr *= (r1);

	Update(0);
}

参考文章

https://zhuanlan.zhihu.com/p/541104837
https://zhuanlan.zhihu.com/p/447895503