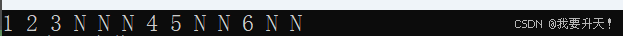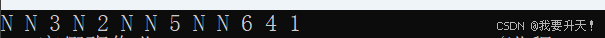二叉树中的前序、中序、后续遍历（C语言）

前序遍历

概念

概念：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
简单点来说就是：根左子树右子树的访问顺序
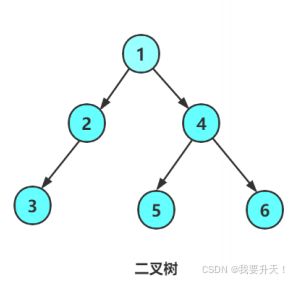
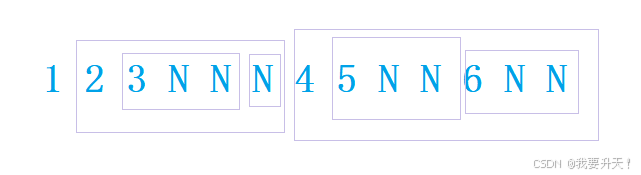
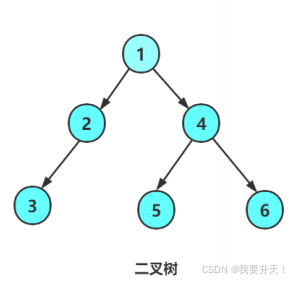
例如：
在这里插入图片描述
这颗二叉树使用前序遍历的结果为：1 2 3 N N N 4 5 N N 6 N N （N表示空）

始终记住，访问顺序为根左子树右子树

代码

节点的结构体

typedef int BTDateType;
typedef struct BinaryTreeNode
{
	BTDateType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

在这里插入图片描述

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

在这里插入图片描述

递归分解图

在这里插入图片描述

这里我只画了一部分，对递归不熟悉的话，可以根据以上的递归图，画出完整的递归图~

中序遍历

概念

概念：中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
简单点来说就是：左子树根右子树的访问顺序
例如：
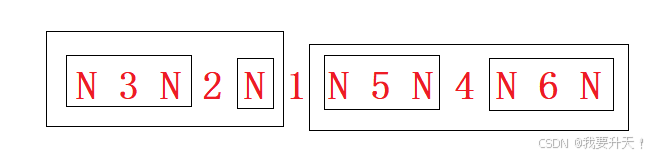
在这里插入图片描述
这颗二叉树使用中序遍历的结果为：N 3 N 2 N 1 N 5 N 4 N 6 N （N表示空）

始终记住，访问顺序为左子树根右子树

代码

节点的结构体

typedef int BTDateType;
typedef struct BinaryTreeNode
{
	BTDateType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

在这里插入图片描述

void InOreder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOreder(root->left);
	printf("%d ", root->val);
	InOreder(root->right);
}

在这里插入图片描述

后序遍历

概念

概念：后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
简单点来说就是：左子树右子树根的访问顺序
例如：
在这里插入图片描述
这颗二叉树使用后序遍历的结果为：N N 3 N 2 N N 5 N N 6 4 1 （N表示空）

始终记住，访问顺序为左子树右子树根

代码

节点的结构体

typedef int BTDateType;
typedef struct BinaryTreeNode
{
	BTDateType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

在这里插入图片描述

void BackOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	BackOrder(root->left);
	BackOrder(root->right);
	printf("%d ", root->val);
}

在这里插入图片描述
注意：由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。