目录
一、刷题ing
1、梯形面积
题目描述:
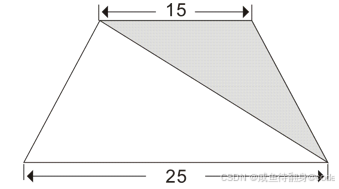
在梯形中阴影部分面积是150平方厘米,求梯形面积。
输出格式
输出梯形面积(保留两位小数)。
#include<stdio.h>
//阴影面积150平方厘米,求梯形面积
//阴影部分为三角形
int main(){
double area(double h,double d1,double d2);
double d1 = 15;
double d2 = 25;
double h = 150 * 2 / d1;
printf("%.2f\n",area(h,d1,d2));
}
double area(double h,double d1,double d2){
double S = (d1 + d2) *h / 2;
return S;
}2、牛吃牧草(数学问题)
题目描述:
有一个牧场,牧场上的牧草每天都在匀速生长,这片牧场可供15头牛吃20天,或可供20头牛吃10天,那么,这片牧场每天新生的草量可供几头牛吃1天?
输出格式
如题所述,牛的数量。
#include<stdio.h>
//每天新生的草量:newNum
//牧场原本的草量:origin
//一头牛每天能吃的草量:eatNum
/*
origin + newNum * 20 = eatNum * 300
origin + newNum * 10 = eatNum * 200
最终得出:newNum = 10 * eatNum 即
每天新生的草量可供十头牛吃一天
*/
int main(){
printf("10");
}3、格式控制
题目描述
依旧是输入三个整数,要求按照占8个字符的宽度,并且靠左对齐输出
输入格式
一行三个整数,空格分开
输出格式
输出它们按格式输出的效果,占一行
样例输入
123456789 -1 10
样例输出
123456789-1 10
#include<stdio.h>
int main(){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
printf("%-8d%-8d%-8d",a,b,c);
}“%-8d”是C语言中
printf函数的格式化字符串的一部分,用于控制输出整数的格式。具体含义如下:
- “%d”表示输出一个十进制整数。
- “-”表示左对齐。如果没有这个符号,默认是右对齐。
- “8”表示输出的字段宽度为8个字符的空间。如果输出的整数位数小于8位,则在左边用空格补齐;如果大于8位,则按照实际位数输出。
4、拆分位数
题目描述:
拆分一个三位数的个位、十位、百位!
你已经完全可以做了哦!输入格式:
输入一个三位数
输出格式:
逆序输出这个三位数,输出个位、十位、百位,三个数字,用空格分开
#include<stdio.h>
/*
个位 n % 10
十位 n / 10 % 10
百位 n / 100
*/
int main(){
int n;
scanf("%d",&n);
printf("%d %d %d",n % 10,n / 10 % 10,n / 100);
}5、陶陶摘苹果
题目描述:
陶陶家的院子里有一棵苹果树,每到秋天树上就会结出10个苹果。苹果成熟的时候,陶陶就会跑去摘苹果。陶陶有个30厘米高的板凳,当她不能直接用手摘到苹果的时候,就会踩到板凳上再试试。
现在已知10个苹果到地面的高度,以及陶陶把手伸直的时候能够达到的最大高度,请帮陶陶算一下她能够摘到的苹果的数目。假设她碰到苹果,苹果就会掉下来。
输入格式:
输入包括两行数据。第一行包含10个100到200之间(包括100和200)的整数(以厘米为单位)分别表示10个苹果到地面的高度,两个相邻的整数之间用一个空格隔开。第二行只包括一个100到120之间(包含100和120)的整数(以厘米为单位),表示陶陶把手伸直的时候能够达到的最大高度。
输出格式:
输出包括一行,这一行只包含一个整数,表示陶陶能够摘到的苹果的数目。
#include<stdio.h>
int main(){
int h;
int count = 0;
int apple[10];
for(int i = 0; i < 10 ; i++){
scanf("%d",&apple[i]);
}
scanf("%d",&h);
for(int j = 0; j < 10 ; j++){
if( (h + 30) >= apple[j] ){
count++;
}
}
printf("%d",count);
}
二、数据结构与算法
初步了解:
- 数据结构:组织和存储数据的方式
- 算法:在有限时间内为解决问题而设计的一组指令和操作步骤
- 复杂度:评估算法效率,分为时间复杂度和空间复杂度
迭代:一种重复执行某种任务的控制结构(for循环、while循环、嵌套循环等)
递归:通过函数调用自身来解决问题。
- 递,即程序不断深入地调用自身,通常传入更小或者简化的参数,直到达到“终止条件”。
- 归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
迭代是在自下而上的解决问题,从基础的步骤开始不断重复累加这些步骤,直至任务完成。
递归是在自上而下的解决问题,将原问题分解为更小的问题,这些子问题和原问题具有相同的形式,接下来将子问题继续分为更小的子问题,直至到达解是已知的基本情况为止。
时间复杂度:分析统计的不是算法运行时间,而是算法运行时间随着数据量变大时的增长趋势。
如何确定渐近上界 ?
1、统计操作数量
- 忽略 T(n) 中的常数项。因为它们都与 n 无关,所以对时间复杂度不产生影响。
- 省略所有系数。例如,循环 2n 次、5n+1 次等,都可以简化记为 n 次,因为 n 前面的系数对时间复杂度没有影响。
- 循环嵌套时使用乘法。
2、判断渐进上界
时间复杂度由 T(n) 中最高阶的项来决定。这是因为在 n 趋于无穷大时,最高阶的项将发挥主导作用,其他项的影响都可以忽略。
设输入数据大小为 n ,常见的时间复杂度类型如下所示(按照从低到高的顺序排列)
常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 指数阶 < 阶乘阶
注意:算法的时间效率往往不是固定的,而是与输入数据的分布有关
空间复杂度:用于衡量算法占用内存空间随着数据量变大时的增长趋势
一般情况下,空间复杂度的统计范围是“暂存空间”加上“输出空间”。
暂存空间可以进一步划分为三个部分。
- 暂存数据:用于保存算法运行过程中的各种常量、变量、对象等。
- 栈帧空间:用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
- 指令空间:用于保存编译后的程序指令,在实际统计中通常忽略不计。
在分析一段程序的空间复杂度时,我们通常统计暂存数据、栈帧空间和输出数据三部分。
设输入数据大小为 n ,下面展示了常见的空间复杂度类型(从低到高排列)。
常数阶 < 对数阶 < 线性阶 < 平方阶 < 指数阶