1.插入排序
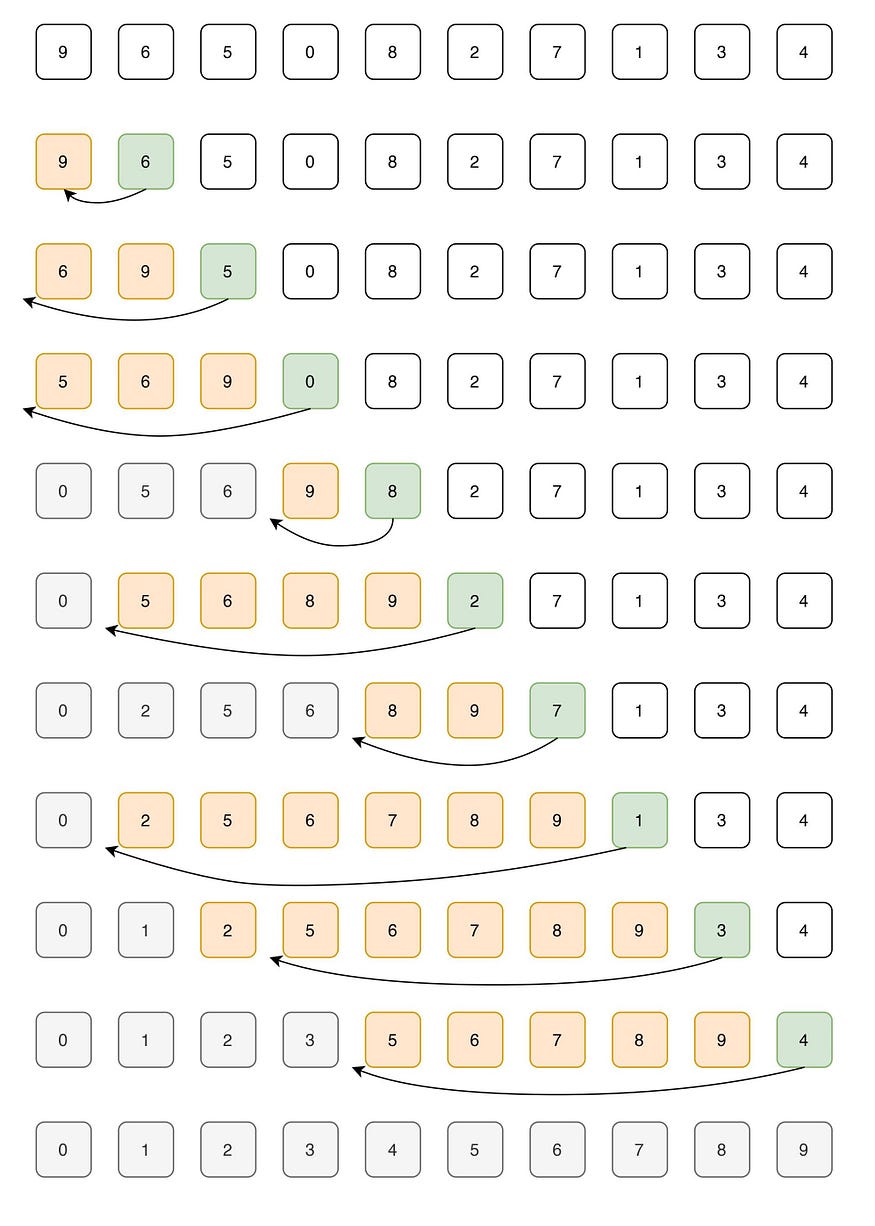
插入排序是一种简单的排序算法,其工作原理类似于对手中的扑克牌进行排序。该数组实际上分为已排序部分和未排序部分。未排序部分的值被拾取并放置在已排序部分的正确位置。当问题规模较小(因为它的开销较低)或当数据接近排序时(因为它是自适应的),插入排序速度很快并且最适合。
示例:
elements: 9, 6, 5, 0, 8, 2, 7, 1, 3, 4
i : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
让我们循环 for i = 1(数组的第二个元素)到 9(数组的最后一个元素)
我=1。由于 6 小于 9,因此移动 9 并在 9 之前插入 6
6 , 9, 5, 0, 8, 2, 7, 1, 3, 4
我=2。由于 5 小于 6 和 9,因此将 5 移到 6 和 9 之前
5, 6, 9, 0, 8, 2, 7, 1, 3, 4
我=3。由于 0 小于 5,6 和 9,因此将 0 移到 5,6,9
0, 5, 6, 9, 8, 2, 7, 1, 3, 4之前
我=4。由于 8 小于 9,因此将 8 移到 9 之前
0, 5, 6, 8, 9, 2, 7, 1, 3, 4
我=5。由于 2 小于 5,6,8 和 9,因此将 2 移到 5,6,8,9
0, 2, 5, 6, 8, 9, 7, 1, 3, 4之前
我=6。0, 2, 5, 6, 7, 8, 9, 1, 3, 4
i=7。0, 1, 2, 5, 6, 7, 8, 9, 3, 4
i=8。0, 1, 2, 3, 5, 6, 7, 8, 9, 4
i=9。0、1、2、3、4、5、6、7、8、9
插入排序
算法:
插入排序(A)
{
for j=i to A.length
key = A[i];
// 将 A[i] 插入已排序序列 A[1,2,3,..,i-1]
j= i-1;
while (j>0 且 A[j]>key)
A[j+1] = A[j]
j= j-1
A[j+1] = key
}
// C program for insertion sort
#include <math.h>
#include <stdio.h>
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
/* Driver program to test insertion sort */
int main()
{
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
2. 选择排序
选择排序算法通过从未排序的部分中重复查找最小元素(考虑升序)并将其放在开头来对数组进行排序。该算法在给定数组中维护两个子数组:
- 已经排序的子数组
- 剩余未排序的子数组
在选择排序的每次迭代/传递中,都会从未排序的子数组中选取最小元素(考虑升序)并将其移至已排序的子数组。选择排序具有最小化交换次数的特性。因此,当交换成本较高时,它是最佳选择。
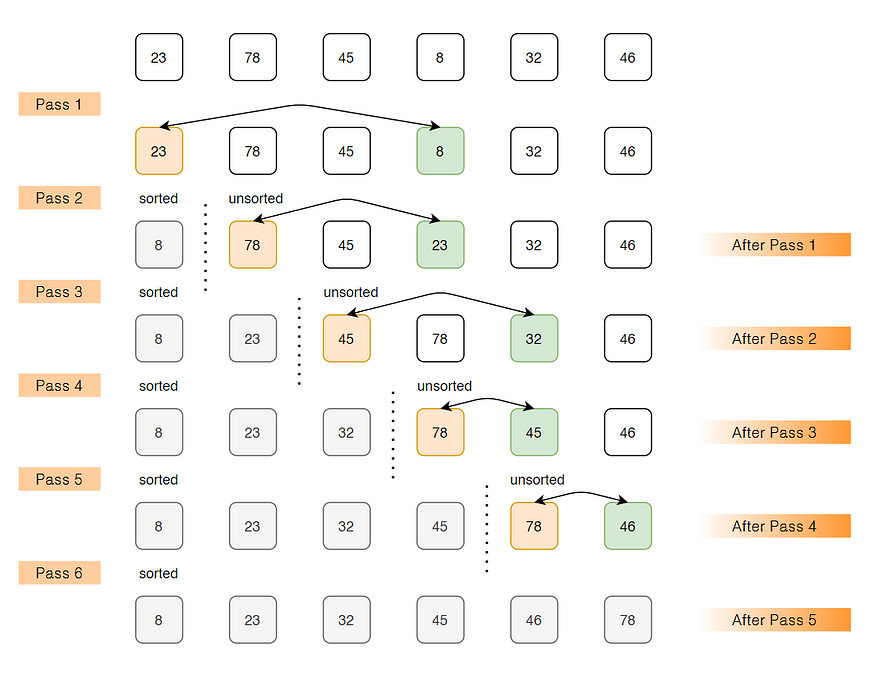
示例:
arr[]= 23 78 45 8 32 46
Pass 1
// 找到arr[0...5]中的最小元素并将其放在开头
8 78 45 23 32 46
Pass 2
// 找到arr[1...5]中的最小元素并将其放在arr[1...5]的开头
8 23 45 78 32 46
Pass 3
// 找到arr[2...5]中的最小元素并将其放在arr[2...5]的开头
8 23 32 78 45 46
Pass 4
// 找到arr[3...5]中的最小元素并将其放在arr[3...5]的开头
8 23 32 45 78 46
Pass 5
// 找到arr[4...5]中的最小元素并将其放在arr[4...5]的开头
8 23 32 45 46 78
选择排序
算法:
void SelectionSort (int a[], int n)
{
int i,j, temp, min;
for (i=0; i<n-1; i++)
{
min = i;
for (j=i+1; j<n; j++)
if (a[j] < a[min])
{
min = j;
}
温度 = a[i];
a[i] = a[min];
a[分钟] = 温度;
}
}
// C program for implementation of selection sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n - 1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr) / sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
3.冒泡排序
冒泡排序是一种排序算法,如果相邻元素的顺序错误,则重复交换相邻元素。每次迭代或传递后,最大的元素到达末尾(在升序的情况下)或最小的元素到达末尾(在降序的情况下)。重复遍历列表直到列表被排序。该算法不适合大型数据集,因为其平均和最坏情况复杂度为 Ο(n^2),其中n是项目数
示例:
64 34 25 12 22 11 90
迭代 1:
( 64 34 25 12 22 11 90) -> ( 34 64 25 12 22 11 90),这里,算法比较前两个元素,并从 64 > 34 开始交换。
(34 64 25 12 22 11 90) - > (34 25 64 12 22 11 90),从 64 开始交换 > 25
(34 25 64 12 22 11 90) -> (34 25 12 64 22 11 90),从 64 开始交换 > 12
(34 25 12 64 22 11 90) ) -> (34 25 12 22 64 11 90),从 64 > 22 开始交换
(34 25 12 22 64 11 90) -> (34 25 12 22 11 64 90),从 64 > 11 开始交换
(34 25 12 22 11) 64 90 ) -> (34 25 12 22 11 64 90 ),现在,由于这些元素已经按顺序排列 (90 > 64),算法不会交换它们。
迭代 2:(
34 25 12 22 11 64 90) -> ( 25 34 12 22 11 64 90),从 34 > 25 开始交换
( 25 34 12 22 11 64 90) -> (25 12 34 22 11 64 90),自 34 > 12 起交换(25 12 34 22 11 64 90) -> (25 12 22 34 11 64 90),自 34 > 22 起交换(25 12 22 34 11 64 90) -> (25 12 22 11 34 64 90) ),交换自 34 > 11(25 12 22 11 34 64 90) -> (25 12 22 11 34 64 90),现在,由于这些元素已经按顺序排列 (64 > 34),算法不会交换它们。
迭代 3:
( 25 12 22 11 34 64 90) -> ( 12 25 22 11 34 64 90),从 25 > 12 开始交换
(12 25 22 11 34 64 90) -> (12 22 25 11 34 64 90),自 25 > 22 起交换
(12 22 25 11 34 64 90) -> (12 22 11 25 34 64 90), 自 25 > 11 起交换
(12 22 11 25 34 64 90) -> (12 22 11 25 34 64 90) ),现在,由于这些元素已经按顺序排列 (34 > 25),算法不会交换它们。
迭代 4:
( 12 22 11 25 34 64 90) -> ( 12 22 11 25 34 64 90)
(12 22 11 25 34 64 90) -> (12 11 22 25 34 64 90),从 22 > 11 开始交换
( 12 11 22 25 34 64 90) -> (12 11 22 25 34 64 90)
迭代 5:(
12 11 22 25 34 64 90) -> ( 11 12 22 25 34 64 90),从 12 开始交换 > 11
(11 12 22 25 34 64 90) -> (11 12 22 25 34 64 90)
迭代 6:(
11 12 22 25 34 64 90) -> ( 11 12 22 25 34 64 90)
现在,数组已经排序了,但是我们的算法不知道它是否已完成。该算法需要一整遍而不需要任何交换才能知道它已排序。
迭代7:
( 11 12 22 25 34 64 90) -> ( 11 12 22 25 34 64 90)
(11 12 22 25 34 64 90) -> (11 12 22 25 34 64 90 ) ( 11 12 22 25 34 64 90) -> (11 12 22 25 34 64 90) (11 12 22 25 34 64 90) -> (11 12 22 25 34 64 90) (11 12 22 25 34 64 90) -> (11 12 22 25 34) 64 90) (11 12 22 25 34 64 90 ) -> (11 12 22 25 34 64 90 )
冒泡排序
算法:
Bubble_Sort(int a[], n)
{
int swapped, i, j;
for (i=0; i<n; i++)
{
交换 = 0;
for (j=0; j<ni-1; j++)
{
if (a[j] > a[j+1])
{
交换 (a[j], a[j+1]); }
交换=1; if (交换== 0)
中断 ; } }
// C program for implementation of Bubble sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n-1; i++)
{
swapped = false;
for (j = 0; j < n-i-1; j++)
{
if (arr[j] > arr[j+1])
{
swap(&arr[j], &arr[j+1]);
swapped = true;
}
}
// IF no two elements were swapped by inner loop, then break
if (swapped == false)
break;
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("n");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
4. 归并排序
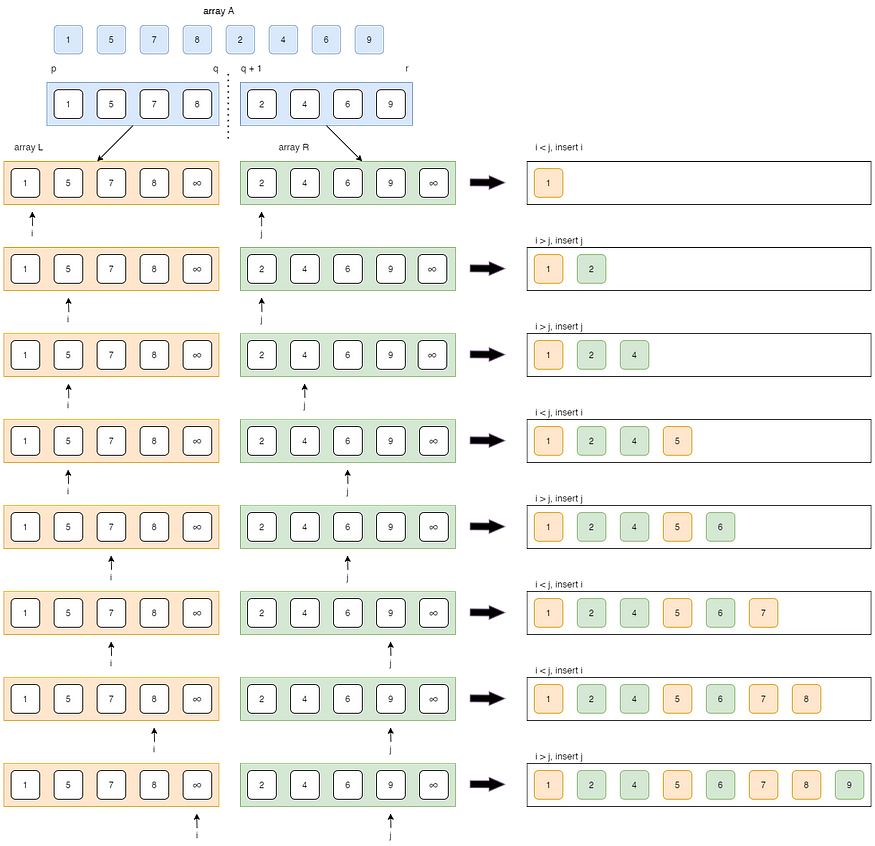
与上述三种排序算法不同,该算法基于分而治之技术。它将输入数组分为两半,为两半调用自身,然后合并已排序的两半。归并排序的核心是函数merge(),用于合并两半。merge(A, p, q, r) 是一个关键过程,它假设 A[p…q] 和 A[q+1…r] 已排序,并将两个已排序的子数组合并为一个。
当您需要稳定且 O(N log N) 排序时,合并排序是唯一的选择。
合并()函数
合并过程也称为异地过程
算法:
merge(A, p, q, r)
{
n1= q-p+1
n2= rq
设 L[1:n+1] 和 R[1:n2+1] 为
(i=1:n1) 的新数组
L[i]= A[p+i-1]
for (j=1:n2)
R[j]= A[q+j]
L[n1 + 1]= 无穷大
R[n2 + 1]= 无穷大
i= 1、j=1
for (k=p:r)
{
if (L[i] <= R[j])
A[k] = L[i]
i= i+1
else
A[k] = R[j ]
j= j+1
}
}
/* C program for Merge Sort */
#include <stdio.h>
#include <stdlib.h>
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
/* create temp arrays */
int L[n1], R[n2];
/* Copy data to temp arrays L[] and R[] */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays back into arr[l..r]*/
i = 0; // Initial index of first subarray
j = 0; // Initial index of second subarray
k = l; // Initial index of merged subarray
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
/* Copy the remaining elements of L[], if there
are any */
while (i < n1)
### 最后的话
最近很多小伙伴找我要Linux学习资料,于是我翻箱倒柜,整理了一些优质资源,涵盖视频、电子书、PPT等共享给大家!
### 资料预览
给大家整理的视频资料:
给大家整理的电子书资料:

**如果本文对你有帮助,欢迎点赞、收藏、转发给朋友,让我有持续创作的动力!**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化的资料的朋友,可以点击这里获取!](https://bbs.csdn.net/topics/618542503)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
hile (i < n1)
### 最后的话
最近很多小伙伴找我要Linux学习资料,于是我翻箱倒柜,整理了一些优质资源,涵盖视频、电子书、PPT等共享给大家!
### 资料预览
给大家整理的视频资料:
[外链图片转存中...(img-IH46Hk3e-1714121534814)]
给大家整理的电子书资料:
[外链图片转存中...(img-VhmtDo16-1714121534815)]
**如果本文对你有帮助,欢迎点赞、收藏、转发给朋友,让我有持续创作的动力!**
**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化的资料的朋友,可以点击这里获取!](https://bbs.csdn.net/topics/618542503)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**