【数据结构】—— 堆

前言

上一章我们学习了二叉树的定义、性质等..现在，我们将要学习二叉树的第一个实际用例——堆。同时，因为堆的“特性”，本章会对排序专题——堆排序进行讲解。本你文所书写的代码大部分为伪代码！没有去具体实现或封装。更多的还是讲解原理和底层。你也可以像之前学习链表、队列、栈一样将堆进行封装。（注：C++提供的priority_queue，该容器的底层就是堆！)

堆的定义

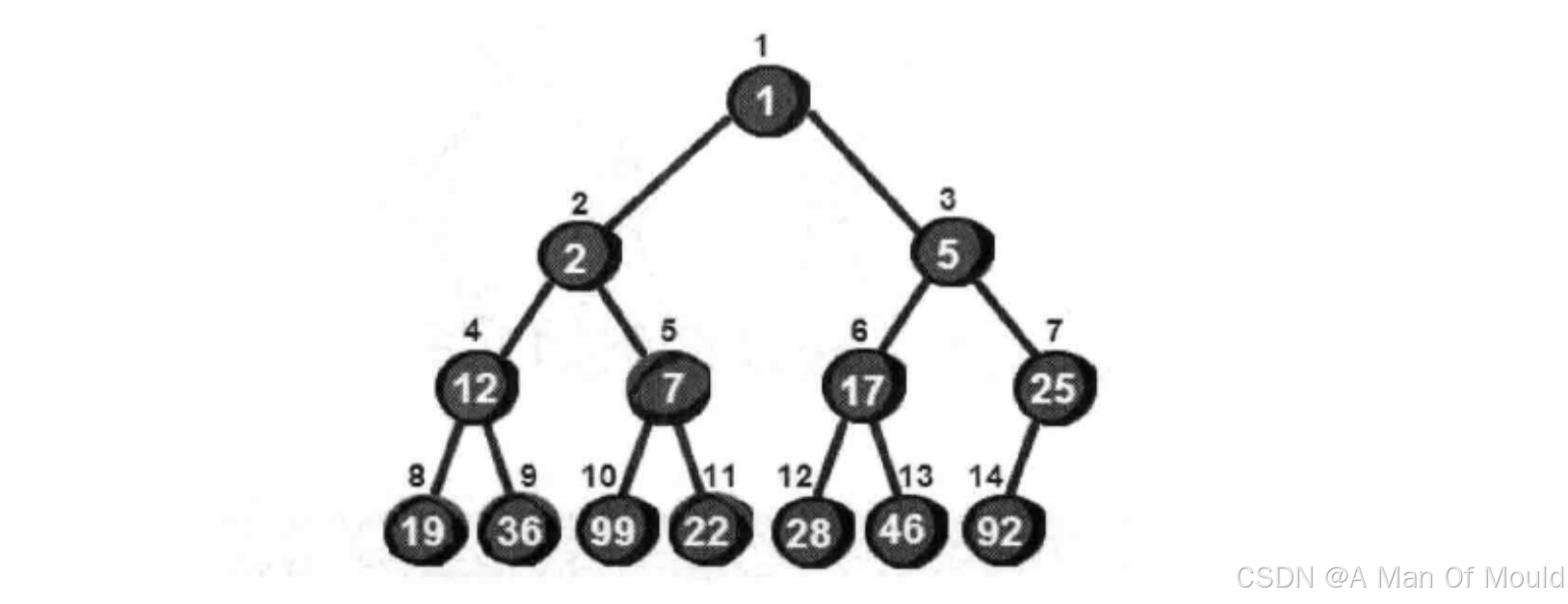
前面我们已经提到过堆是二叉树的用例，所有堆的本质还是一颗二叉树。但是说它是一颗二叉树又不太准确！更严谨的说法：它是一颗完全二叉树，就像下面这颗树一样！！！

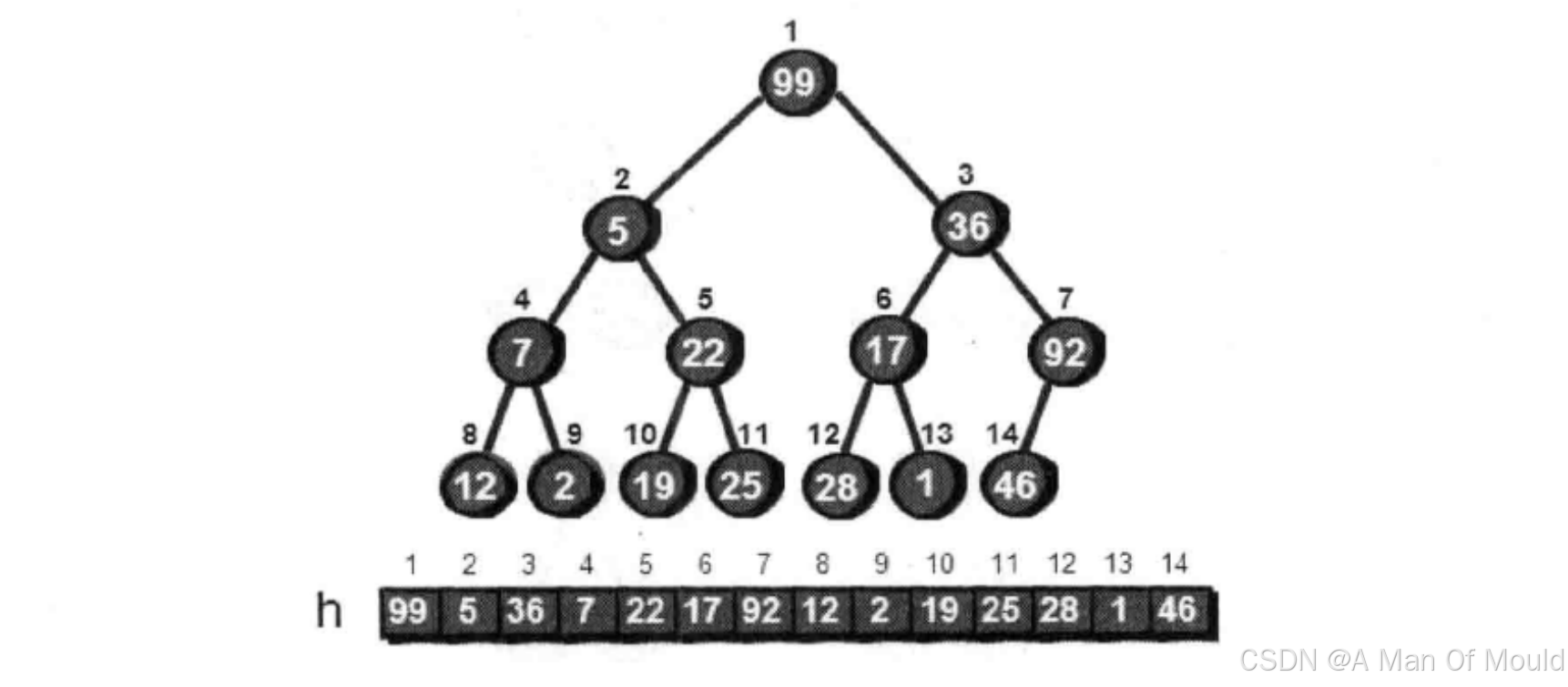
有没有发现这棵完全二叉树有一个特点？就是所有父结点都比其左右子结点要小(注意:圆圈里面的数是值，圆圈上面的数是这个结点的编号)。符合这样特点的完全二叉树我们称为小堆。反之，如果所有父结点都比其左右子结点要大，这样的完全二叉树称为大堆。同时，我们再观察每个结点的编号，是不是全部连续，没有间断！那么因此，堆十分契合我们之前讲过的树的顺序存储结构，因此堆可以利用一个一维数组进行存储，并且从下标为1开始存储数据（这是为了我们后续书写代码提供便利！)。

基于此我们可以给出严格的定义：

堆是具有下列性质的完全二叉树：

每个结点的值都大于或等于其左右孩子结点的值，称为大堆；或每个结点的值都小于或等于其左右孩子结点的值，称为小堆。

基础铺垫

向下调整算法

那么利用大堆、小堆的特性究竟有什么用呢？假如有 14个数，分别是99、5、36、7、22、17、46、12、2、19、25、28、1和92，请找出这14个数中最小的数，请问怎么办呢？最简单的方法就是将这14个数从头到尾依次扫遍，用一个循环就可以解决。这种方法的时间复杂度是O(14)，也就是O(N)跟数据的个数有关。

伪代码实现如下：

	int Min = INT_MAX;
	for (int i = 0; i < N; ++i)
		if (Min > num[i])
			Min = num[i];

现在我们需要删除其中最小的数，并增加一个新添加数 23，再次求这14个数中最小的一个数。请问该怎么办呢？只能重新扫描所有的数，才能找到新的最小的数，这个时间复杂度也是O(N)。假如现在有14次这样的操作(删除最小的数后再添加一个新数)，那么整个时间复杂度就是O(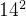 $14^{2}$ )即O( $n^{2}$ )。那有没有更好的方法呢？堆这个特殊的结构恰好能够很好地解决这个问题。

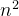
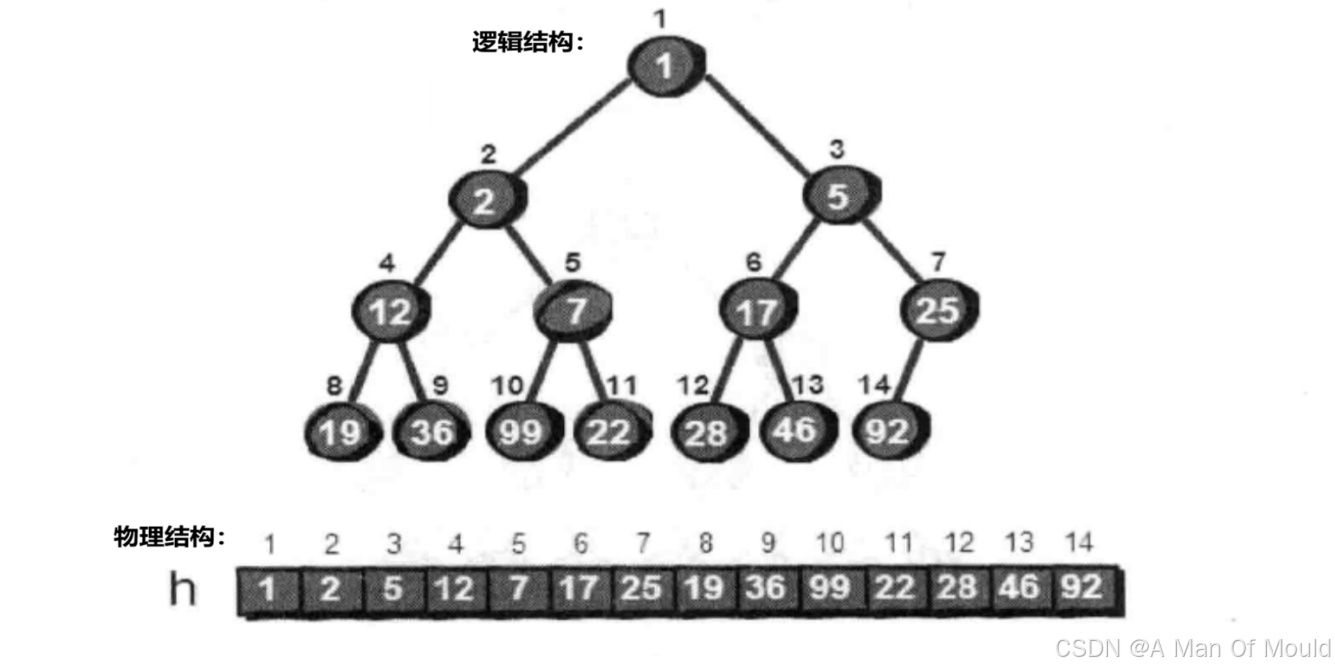
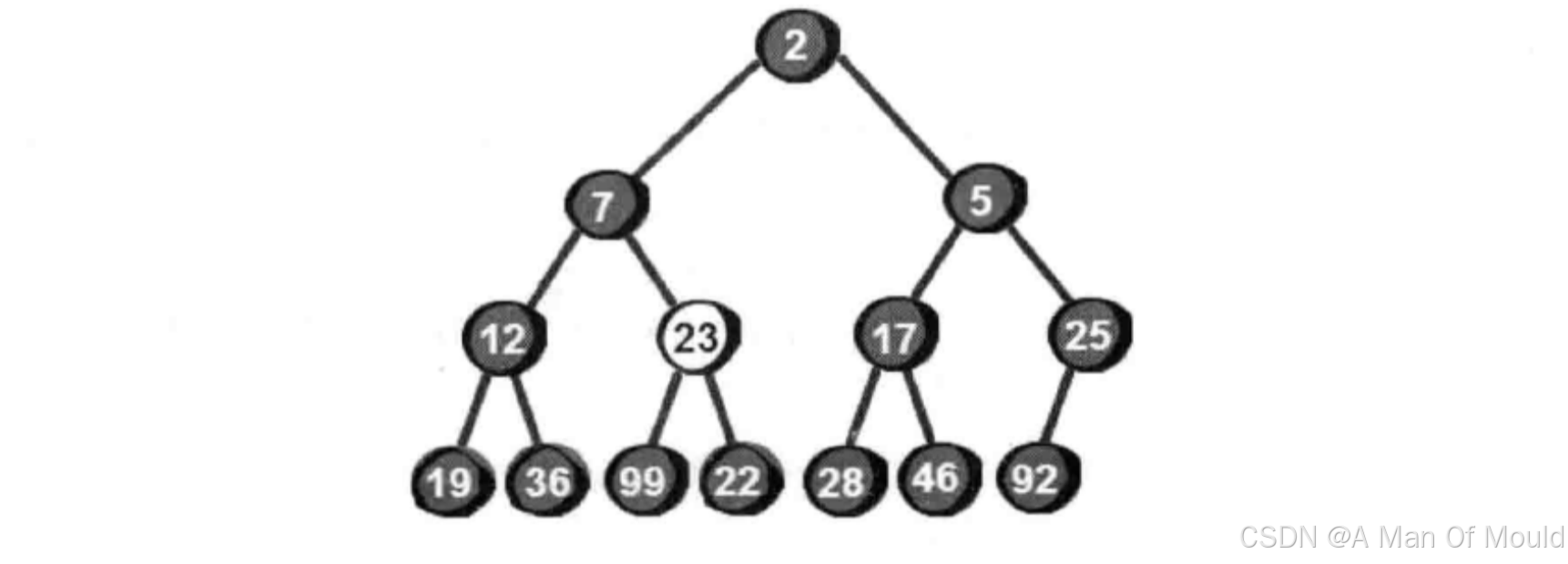
首先我们把这14个数按照最小堆的要求(就是所有父结点都比子结点要小)放入一棵完全二叉树，就像下面这棵树一样。

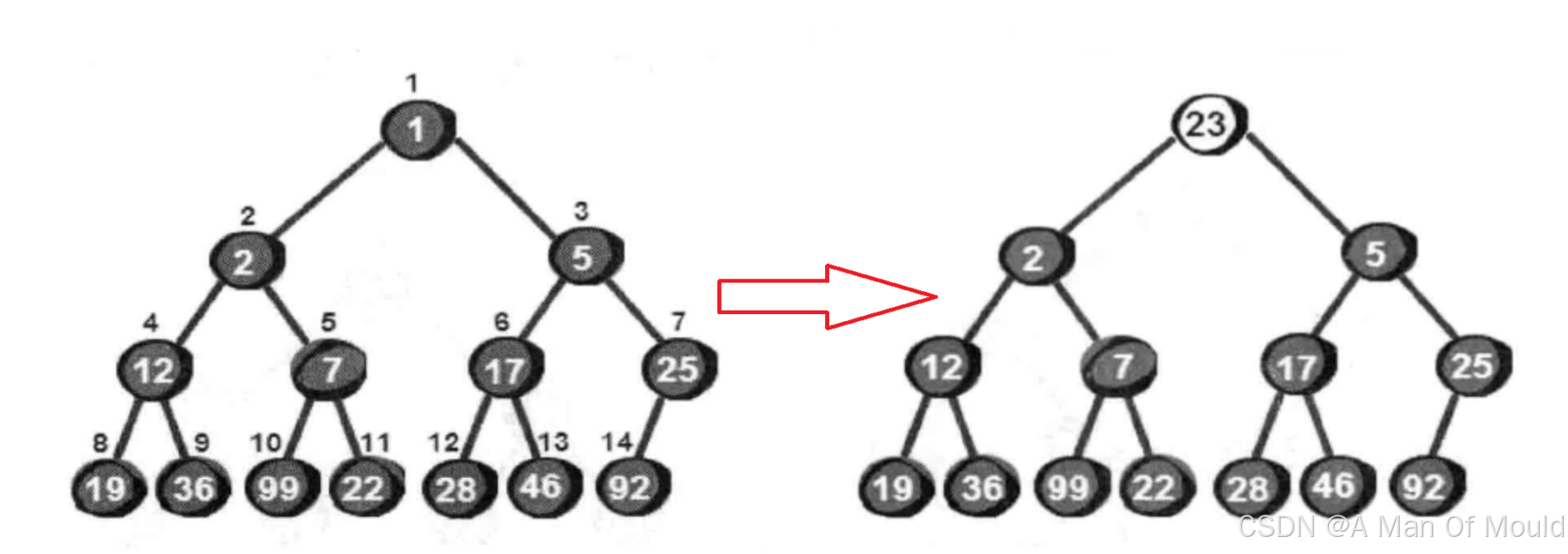
很显然最小的数就在堆顶，假设存储这个堆的数组叫做h的话，最小数就是h[1]。接下来，我们将堆顶部的数删除。将新增加的数23放到堆顶。显然加了新数后已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。那如何调整呢？这就引入堆的一个重要操作：向下调整。

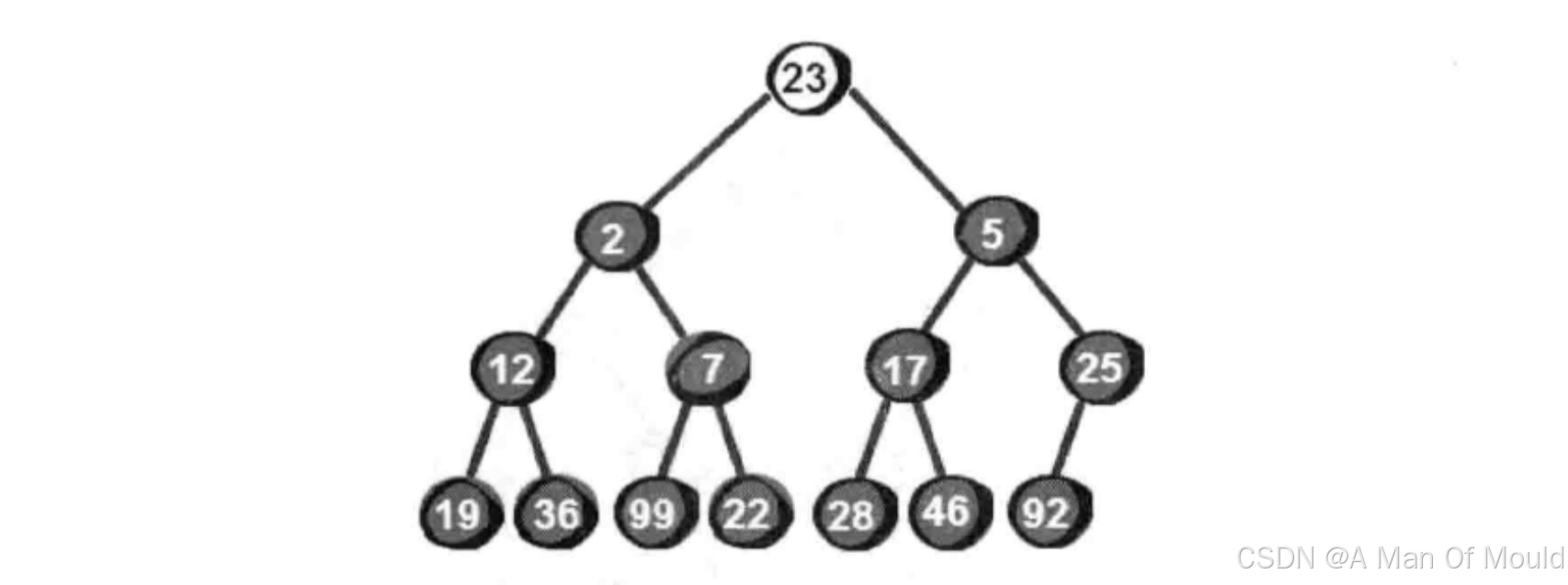
向下调整的具体做法：选择下标为i的那个数作为看成堆顶，将堆顶的数和堆顶的左右孩子进行比较，如果当前堆顶的数小于左右孩子中较小的那一个，那么说明当前的堆符合小堆的性质，停止调整。反之，则将堆顶的元素和较小元素进行交换，重复上述操作，直到堆顶的元素符合小堆的特性！调整案例如下所示：假设在将小堆的堆顶元素替换成23，那么该如何调整这个小堆呢？

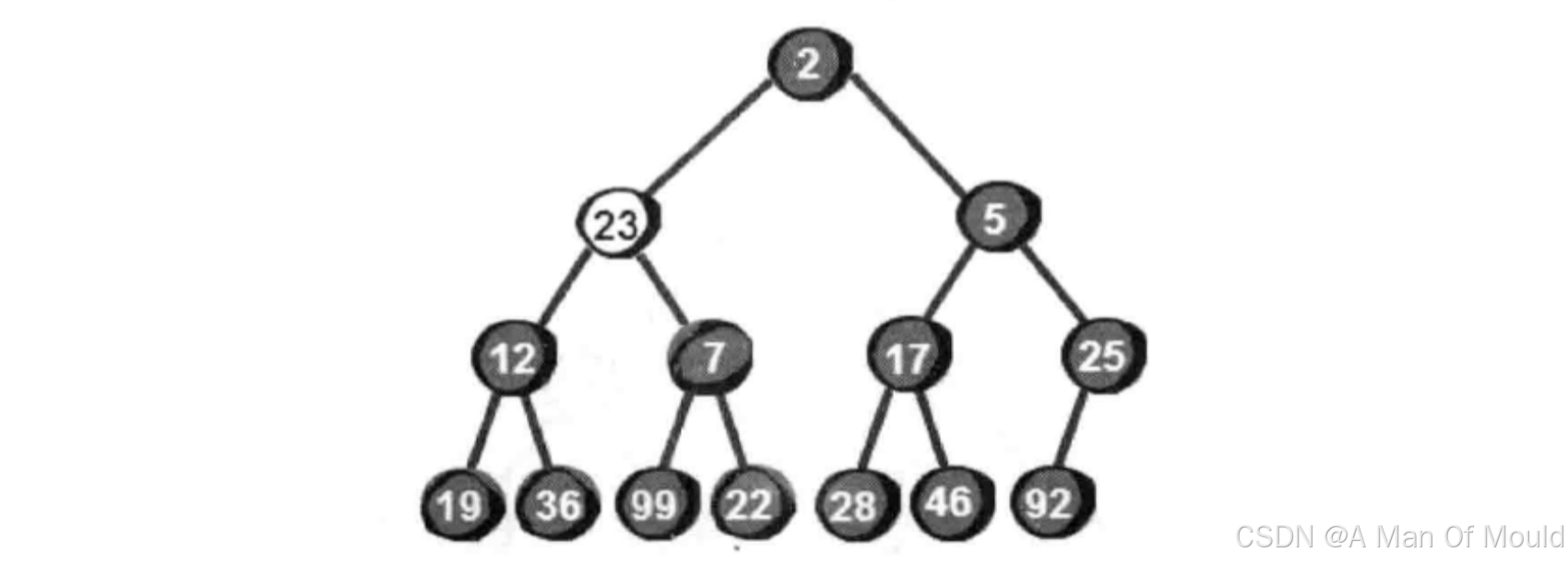
向下调整，我们需要将这个数和它的左右孩子（2，5)进行比较，选择较小的一个个它进行交换。交换结果如下。

我们发现此时还是不符合小堆的特性，因此还需要继续向下调整。于是继续将23与它的两个左右孩子12和7比较，选择较小一个交换，交换之后如下。

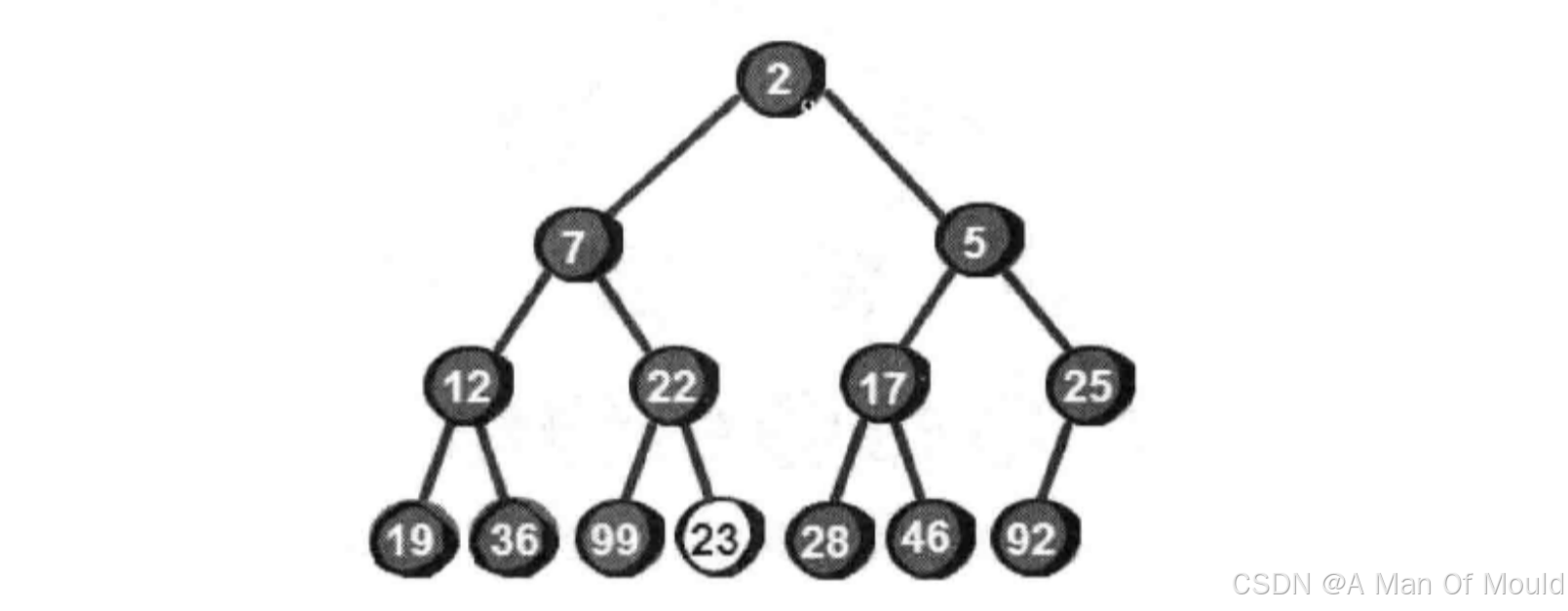
到此，还是不符合小堆的特性，仍需要继续向下调整，直到符合小堆的特性为止。

现在我们发现已经符合小堆的特性了。综上所述，当新增加一个数被放置到堆顶时，如果此时不符合最小堆的特性，则需要将这个数向下调整，直到找到合适的位置为止，使其重新符合最小堆的特性。

向下调整的思路已经理清了！那就剩代码的实现。首先我们先思考一下，假设我们知道一个数据的准确下标，那么这么知道它的左右孩子的下标呢？回到二叉树的性质解决这个问题，假设现在当前的元素的下标为i，那么它的左孩子的下标为：2 * i；右孩子的下标为：2 * i + 1，（看下面这个图的序号，自己推导一下）

那就很好写了！只要注意下标的限制即可，代码如下所示：

// i：开始调整的下标, n：堆的元素个数，即数组的有效元素个数
void AdjustDown(int* h, int i, int n)
{
	int heapTop = i;
	//判断当前结点是否存在左孩子
	while (2 * heapTop <= n)
	{
		int minChildIndex = 2 * heapTop;

		if (2 * heapTop + 1 <= n)//判断右孩子是否存在
		{
			//记录左右孩子较小的下标
			if (h[minChildIndex] > h[2 * heapTop + 1]) 
				minChildIndex = 2 * heapTop + 1;
		}
		if (h[heapTop] > h[minChildIndex])
		{
			//交换元素
			swap(h[minChildIndex], h[heapTop]);//偷个懒，直接调用C++现成的接口
			//迭代
			heapTop = minChildIndex;

		}
		else
			break;
	}
}

我们刚才在对 23进行调整的时候，只进行了3次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶，为2。而使用之前从头到尾扫描的方法需要14次比较，现在只需要3次就够了。也就是说，对一个堆顶元素进行调整，最多只需要调整这颗完全二叉树的深度即可。根据二叉树的性质可知，二叉树的深度为O(logN)，即向下调整的时间复杂度为O(logN)。

向上调整算法

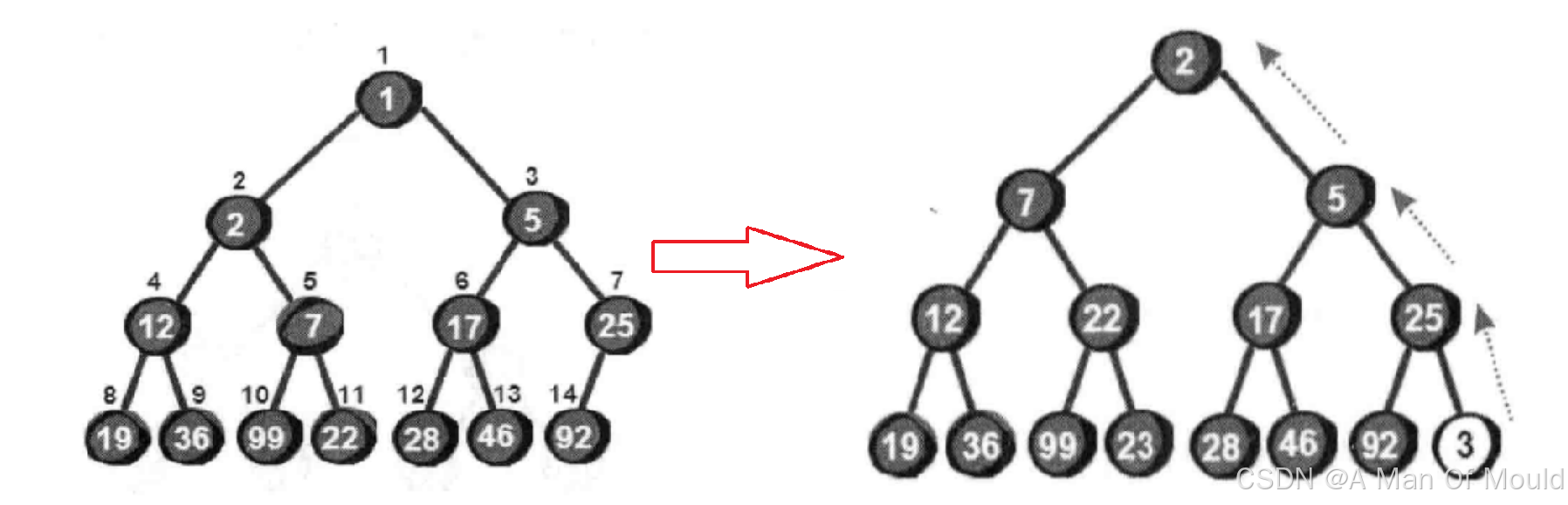
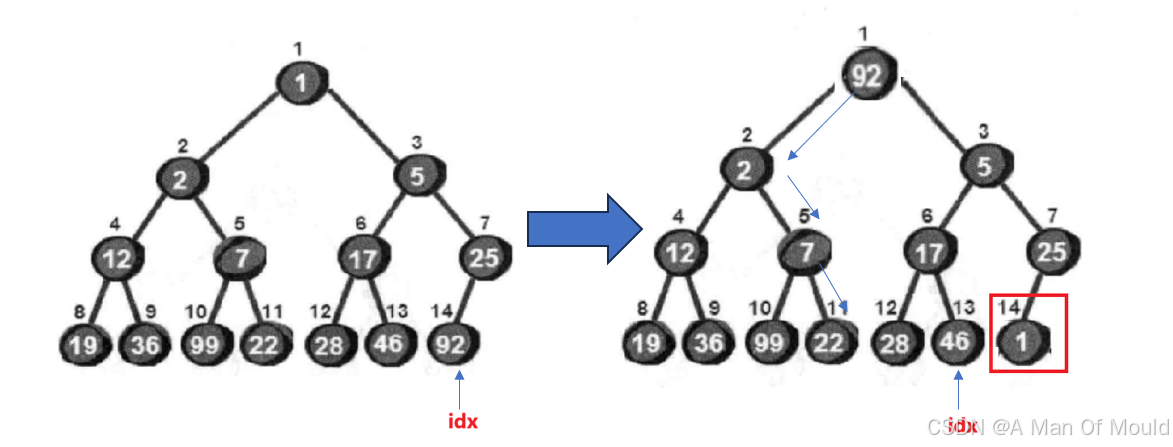
说到这里，如果只是想新增一个值，又该如何操作呢？即如何在原有的堆上直接插入一个新元素呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为N(即有N个元素)，那么插入一个新元素所需要的时间为O(logN)。例如我们现在要新增一个数3。

先将3与它的父结点25比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点5小，因此再次与父结点交换，到此又重新满足了最小堆的特性。向上调整代码实现如下：

void AdjustUp(int* h, int i, int n)
{
	int parent = i / 2;
	while (i > 1)
	{
		//如果当前结点的值大于父结点的值，说明不符合小堆的特性
		if (h[parent] > h[i])
		{
			//交换
			swap(h[parent], h[i]);
			//迭代
			i = parent;
			parent = i / 2;

		}
		else 
			break;
	}
}

堆的核心操作

建堆(build heap)

我们前面铺垫了这么多，现在到了检验成果的时候到了！首先要对堆进行操作的前提是有堆啊。那么摆在我们面前的第一个问题是这么建堆？

回到之前的案例，直接把 99、5、36、7、22、17、46、12、2、19、25、28、1和 92这 14个数放入一个完全二叉树中(这里我们还是用一个一维数组来存储完全二叉树)。

在这棵完全二叉树中，我们从最后一个结点开始，依次判断以这个结点为根的子树是否符合小堆的特性。如果所有的子树都符合小堆的特性，那么整棵树就是小堆了。首先我们从叶结点开始。因为叶结点没有儿子，所以所有以叶结点为根结点的子树(其实这个子树只有一个结点)都符合小堆的特性，即父结点的值比子结点的值小。这里所有的叶结点连子结点都没有，当然符合这个特性。因此所有叶结点都不需要处理，直接跳过。从第n/2个结点(n为完全二叉树的结点总数，这里即7号结点)开始处理这棵完全二叉树。注意完全二叉树有一个性质：最后一个非叶结点是第n/2个结点。所有基于该特性，我们从起始位置定为n /2，即i= n /2; 从起始位置开始调用向下调整算法，直到i == 1；代码实现逻辑如下：

for (int i = n / 2; i >= 1; --i)
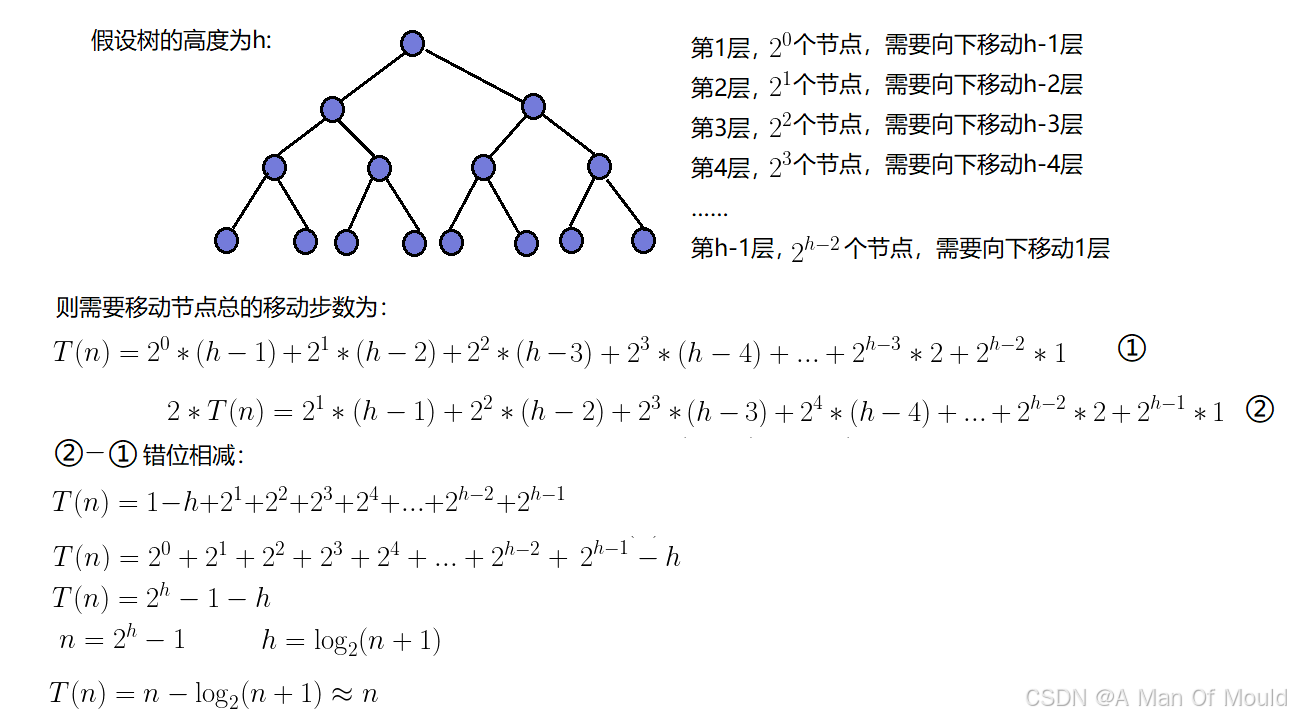
	AdjustDown(h, i, n);

小结一下这个创建堆的算法。把n个元素建立一个堆，首先我可以将这n个结点以自顶向下、从左到右的方式从1到n编码。这样就可以把这n个结点转换成为一棵完全二叉树。紧接着从最后一个非叶结点(结点编号为n/2)开始到根结点(结点编号为1)，逐个扫描所有的结点，根据需要将当前结点向下调整，直到以当前结点为根结点的子树符合堆的特性。而这个建堆的时间复杂度为O(n)，证明如下：（高中知识：错位相减——等差 * 等比数列）

堆的插入(heap insert)

堆的插入其实已经讲过了，在讲解向上调整算法的时候，我们就是举例在原有的堆上插入元素。回顾一下，要在原有的堆上插入新的元素，直接在插入到数组的末尾上，再调用向上调整算法即可。

代码实现如下：

void heapInsert(int* h, int x)
{
    /*
    idx：标记插入位置
    假设现在堆中有7个元素，那么新插入的元素的下标应该为h[8],
    8又代表了插入新的元素后，堆的元素个数
    */
	h[++ idx] = x;
	AdjustUp(h, idx -1, idx);
	++idx;
}

堆的删除(heap erase)

删除堆是删除堆顶的数据，将堆顶的数据跟最后一个数据一换，然后删除数组最后一个数据，再从堆顶(i = 1)进行向下调整算法。

代码实现如下：

void heapErase(int* h)
{
	swap(h[1], h[idx]);
	--idx;
	AdjustDown(h, 1, idx);
}

当然，如果你想也可以实现一个任意位置的删除操作，和删除堆顶元素的操作一样！只是调整的位置差异而已！

堆的应用

堆排序

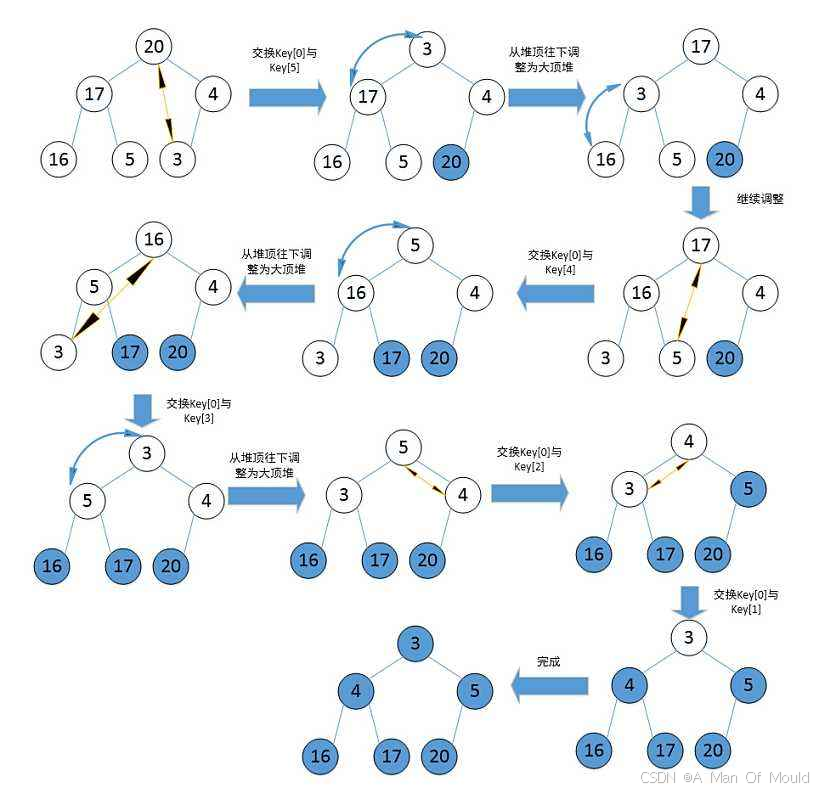
堆排序(Heap Sort)就是利用堆(假设利用大堆)进行排序的方法。它的基本思想是，将待排序的序列构造成一个大堆。此时，整个序列的最大值就是堆顶的元素。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)，然后将剩余的 n-1个序列重新构造成一个堆，这样就会得到n个元素中的次小值。如此反复执行，便能得到一个有序序列了。

这个图就很全面解释了堆排序的过程和思想（COPY的）

基于此思想，代码实现如下:

void heapSort(int num[], int n)
{
	for (int i = n / 2; i >= 1; --i)
		AdjustDown(num, i, n);
	while (n > 1)
	{
		swap(num[1], num[n]);
		--n;
		AdjustDown(num, 1, n);
		
	}
}

现在来分析一下堆排序的时间复杂度。我们首先要对需排列的序列进行建堆，建堆的时间复杂度为O(n)，之后在这个堆的基础上不断进行删除堆顶元素，删除操作的时间复杂度为O(logn)，需要进行删除操作n次（n为序列的长度、或元素的个数)，所有总的时间复杂度为O(n * (logn + 1))，即堆排序的时间复杂度为O(n * logn)。

OK，最后还是要总结一下。像这样支持插入元素和寻找最大(小)值元素的数据结构称为优先队列（也叫堆)。如果使用普通队列来实现这两个功能，那么寻找最大元素需要枚举整个队列，这样的时间复杂度比较高。如果是已排序好的数组，那么插入一个元素则需要移动很多元素，时间复杂度依旧很高。而堆就是一种优先队列的实现，可以很好地解决这两种操作。另外 Diikstra算法（——最短路径，在图的章节，我们会来学习！）也可以用堆来优化。

堆还经常被用来求一个含有n个数的序列中第K大的数（简称Top-K问题），只需要建立一个大小为K的小堆，堆顶就是第K大的数。(我举个例子，假设有10个数，要求第3大的数。第一步选取任意3个数，比如说是前3个，将这3个数建成最小堆，然后从第4个数开始，与堆顶的数比较，如果比堆顶的数要小，那么这个数就不要，如果比堆顶的数要大，则舍弃当前堆顶而将这个数做为新的堆顶，并再去维护堆（向下调整算法），用同样的方法去处理第5~10个数)如果求一个数列中第K小的数，只需要建立一个大小为K的大堆，堆顶就是第K小的数，这种方法的时间复杂度是O(N * logK)。当然你也可以用堆来求前K大的数和前K小的数。