今天小编在刷题的时候遇见了一道很有意思的题，LCR 022. 环形链表 II - 力扣（LeetCode），这道题的意思是要找出环形链表的入口点。理解这道题的前提首先要先理解快慢指针原理。那么接下来请跟着小编一起分析这道题（如果有错误的地方欢迎大家指出）。

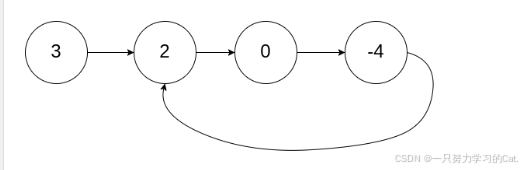
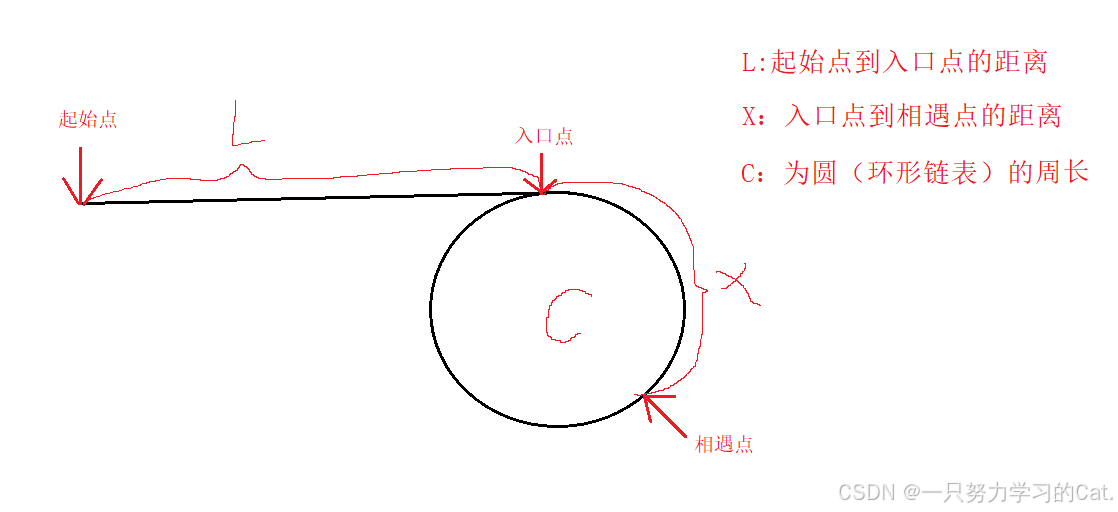
        通过题目给出的示例图，我们可以得知，链表的尾节点指向前面链表的其中某一个节点，这个节点可以在头可以在尾也可以在中间，而我们需要找到链表尾节点的下一个节点及入口循环链表的入口点。那么我们可以画一个逻辑图

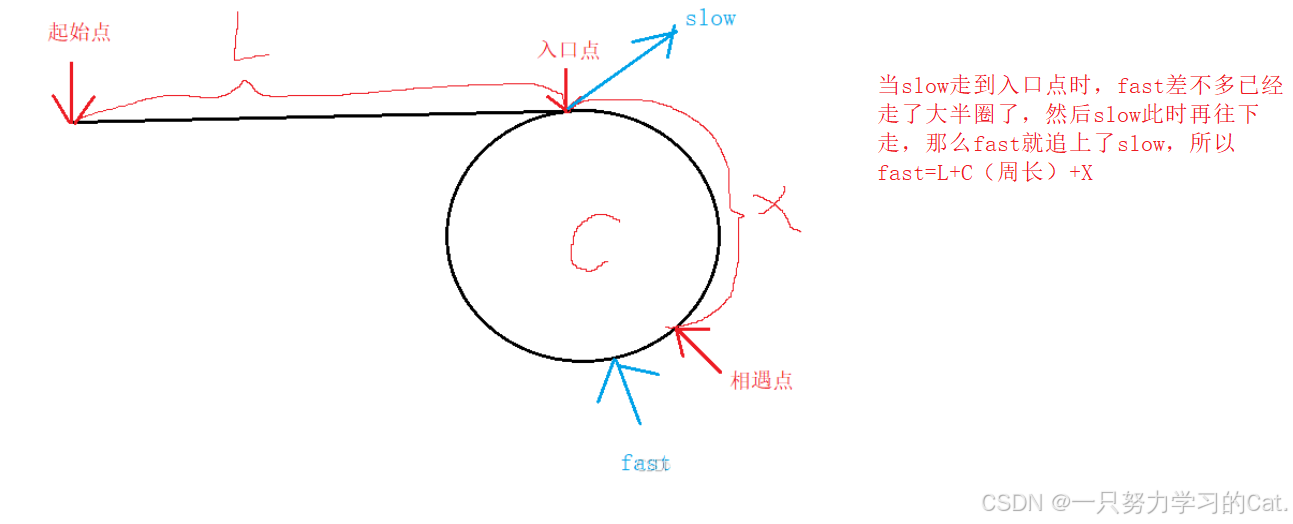
        我们将链表的头节点看作起始点，环状链表起始的点位（尾节点->next）称为入口点，我们会运用到快慢指针。快慢指针最终会相遇（快指针==慢指针），我们将快指针与慢指针相遇的点称为相遇点。

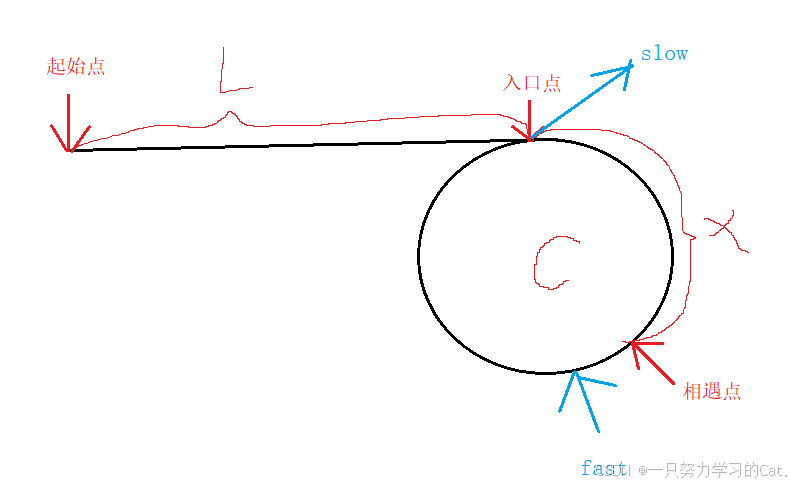
        一开始我们先定义fast与slow,并让他们一开始都指向链表头节点，fast走两步，slow只走一步。

        当slow走到入口点时，假设此时fast的位置在图中标记的地方，这里需要知道由于slow只走一步并且fast只走两步，所以slow必定走不完一个循环，fast会在slow走完一个循环前找到slow。所以X的极限距离=C-1，及0<=X<C。

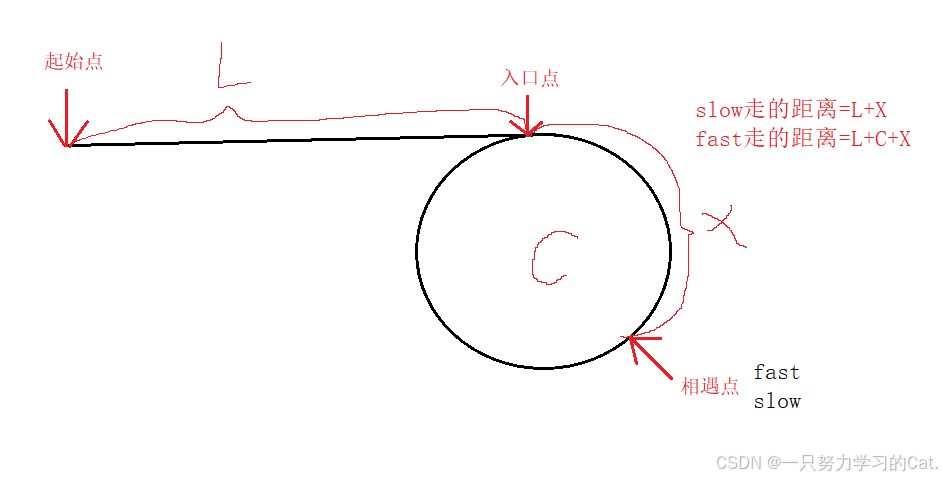
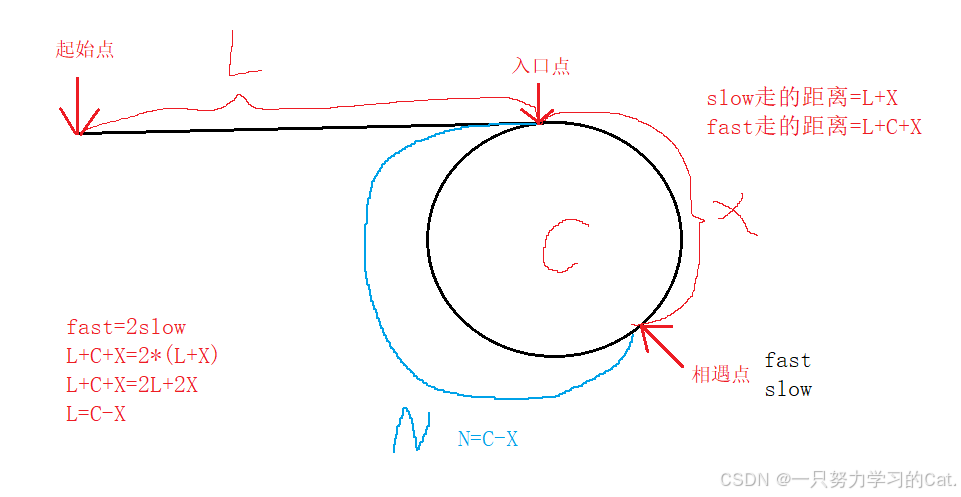
        当slow与fast都到达相遇点时候，此时slow的距离为L+X，而fast为什么是L+C+X呢？

        可以得出一个推断出一个关系式:

        所以在这里就可以推导出结论，一个指针从起始点开始走，一个指针从相遇点开始走，这两个指针会在入口点相遇。

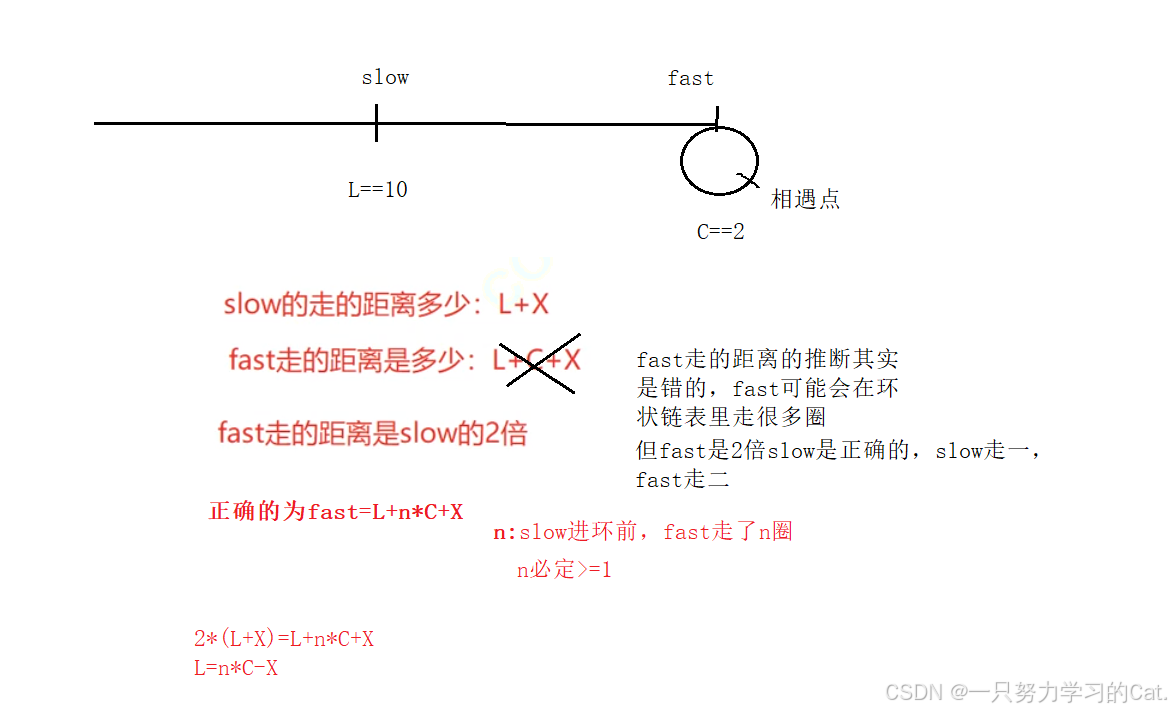
        是不是看到这里有小伙伴说那么这题就是这样分析的，但其实，以上的过程其实是错的，但是结论是正确的。 

        假设L为10，C为2，当fast走到入口点时，slow还要一大段距离要走。

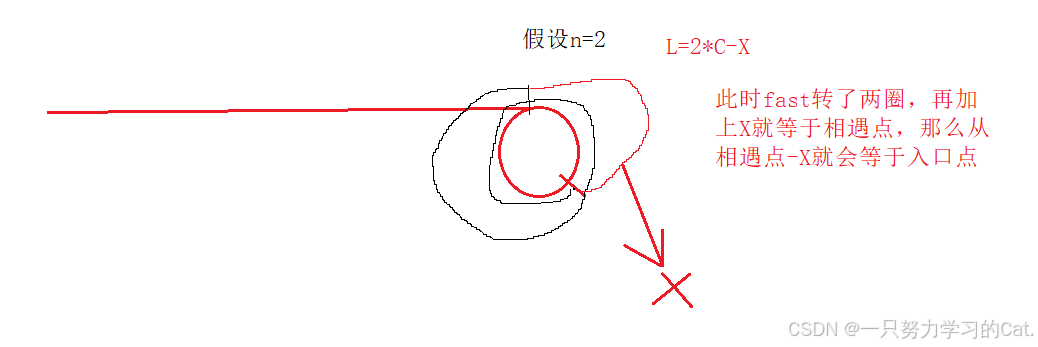
        根据上图的推论最终正确的表达式其实为L=n*C-X。 slow在进环前fast在环里面转了n圈，只是n我们是不知道的。

        在这最后经过前面的正确分析，我们得出最终正确的结论一个指针从起始点开始走，一个指针从相遇点开始走，这两个指针会在入口点相遇。

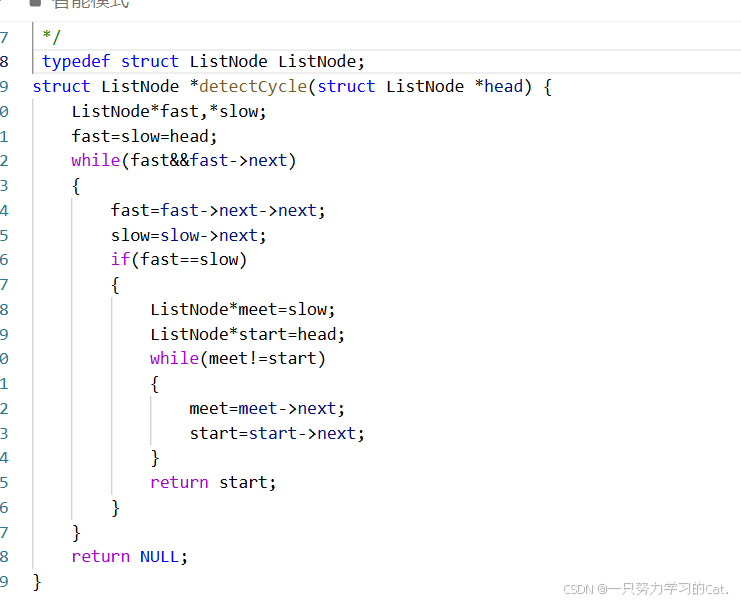
        以下为代码：