1.贪心算法

贪心算法是一种在每一步选择中都采取当前状态下最好或者最优的选择，从而希望导致结果是全局最好或者最优的算策略。贪心算法不保证到最优解，但在某些问题上可以快速找到一个近似解。

 例如在找零钱问题中问题中，买了一样东西36.4元，付款100，找零63.6元，该如何选择币值？显然有多种币值的组合方案。

63.6元=10元*6+1元*3+0.1*6    //15张可用解
63.6=50+10+2+1+0.5+0.1    //6张，最优解

 后者采用的策略是，每次选择一张面值最接近剩余金额的人民币，这是贪心选择策略。

1.1、贪心选择策略

贪心法求解的问题必须有两个性质：最优子结构和贪心选择。

当求解一个问题的最优解时，贪心法将最优子结构问题的求解过程分成若干步骤，每一步都在当下状态做出局部最好选择（称为贪心选择），通过逐步迭代，期望通过各各阶段的局部最优选择获得问题的局部最优解。

下面看一个例子：

求数据序列最小值问题具有最优子结构和贪心选择性质。已知一个数据序列keys有n个元素，采用贪心选择策略，分n步求解如下。

1. 设min表示长度为n+1子序列的最下序号，初值i=0，min=0。
2. 求解过程，i从0~n-1递增，i++，每一步求长度为i+1子序列的最小值，只增加一次比较，若key[i]小于前i个元素的子序列的最小值key[min]，则min=i,记min为最小值。

在逐步求解的过程中，min记载每一步贪心选择的结果，随着子序列的长度递增，min由局部最优选择变成了全局最优解。时间复杂度为O(n).

下面做一个简单的题目来练习一下：

题目：最大子数组和问题

给定一个整数数组nums，找到子数组的最大和。

输入：{-2,1,-3,4,-1,2,1,-5,4};

输出：6

解释：子数组{4，-1,2,1}的和为6；

public class MaxSubArraySum {
    public static void main(String[] args) {
        int[] nums ={-2,1,-3,4,-1,2,1,-5,4};
    }
    public static int maxSubArraySum(int[] nums){
        //初始化最大和为数组的第一个元素
        int maxSum =nums[0];
        //初始化当前的和为0
        int currentSum =0;

        //遍历数组中的每一个元素
        for(int i=0;i<nums.length;i++){
            //如果当前和加上当前元素大于当前元素，说明当前的子数组可以继续扩展
            //否则，重置当前和为当前元素的值
            currentSum=Math.max(nums[i],currentSum+nums[i]);
            maxSum=Math.max(maxSum,currentSum);

        }
        //返回最大子数组的和
        return maxSum;
    }
}

这个代码实现了Kadane算法，它是解决最大子数组的高效方法。

kadane算法步骤：

1. 初始化两个变量max_so_far和max_ending_here，max_so_far用于存储到目前为止找到的最大子数组和，max_ending_here用于存储以当前原数结尾的最大子数组和。初始时，两者都设为数组的第一个元素。
2. 遍历数组：从数组的第二个元素开始遍历
3. 更新全局最大和：对于当前元素nums[i]max_ending_here可以是元素本身，或者是加上前一个max_ending_here的值（如果这样更大）。
4.  currentSum=Math.max(nums[i],currentSum+nums[i]);
5. 继续遍历：移动到下一个元素，重复步骤
6. 最后返回最大结果

1.2、贪心算法不是最优解的情况

给定n个活动，每个活动i都有开始时间start[i]和结束时间end[i]。选择最大数量的活动，使得这些活动互不重叠（即一个活动结束后另一个活动开始）。

示例：

活动1：开始时间 1，结束时间 3
活动2：开始时间 3，结束时间 5
活动3：开始时间 0，结束时间 6
活动4：开始时间 5，结束时间 7
活动5：开始时间 8，结束时间 9

如果我们使用贪心算法，可能会按照结束时间对活动进行排序，然后选择第一个活动，再选择结束时间最接近当前活动的活动。按照这个方法，我们可能会选择活动1,2,5，因为他们互不重叠，但只选择了3个活动。

代码演示：

public class GreedyActivitySelection{
   static class Activity implements Comparable<Activity>{
       int start,end;
       public Activity(int start,int end){
           this.start=start;
           this.end=end;
       }

       @Override
       //用于比较两个对象的结束时间
       public int compareTo(Activity other) {
           return this.end-other.end;
       }
   }
   public static int activitySelection(Activity[] activities){
       Arrays.sort(activities);//按照结束时间排序
       int count =1;//至少选择一个活动
       int end =activities[0].end;//用于记录选择最后一个活动的结束时间，初始值为第一个活动的结束时间
       for (int i=1;i<activities.length;i++){
           //如果当前活动开始的时间大于上一个活动的结束时间
           if (activities[i].start>=end){
               count++;
               end=activities[i].end;//更新结束时间
           }
       }
       return count;

   }

    public static void main(String[] args) {
        Activity[] activities = {
                new Activity(1, 3),
                new Activity(3, 5),
                new Activity(0, 6),
                new Activity(5, 7),
                new Activity(8, 9)
        };
        System.out.println("Maximum number of activities that can be performed: " + activitySelection(activities));
    }

    }

1.3、01背包问题

给定一个背包，它的容量为W（正整数）。同时，有n个物品，每个物品都有各自的重量w[i]（正整数）。特别地，每个物品被选取与否只有一次机会，即每个物品只能选取0次或1次，不能分割。任务是在不超过背包容量的前提下，选择一些物品放入背包，使得背包中的物品总重量最大。

示例：

假设背包的容量为 W = 7，有3个物品，重量分别为 w[1] = 3, w[2] = 4, w[3] = 5。

 我们可以选择物品1和物品2，总重量为3 + 4 = 7。
 我们也可以选择物品3，总重量为5。

首先我们要知道，贪心算法并不能得到最优解，因为它不能回溯到之前的选择。

public class GreedyActivitySelection{
    //贪心算法解决01背包问题
    public static int knapsackGreedy(int w,int[] weights,int[] values,int n ){
        //用于存储物品的索引和价值比
        int[][] items =new int[n][2];
        //将物品及其索引存入数组当中
        for (int i =0;i<n;i++){
            items[i][0]=i;//索引
            items[i][1]=values[i]/weights[i];//价值/重量,选择单位重量的方式
        }
        //按价值/重量降序排序
        Arrays.sort(items, (a,b)->b[1]-a[1]);

        int totalValue =0;//总价值
        int currentWeight=0;//当前背包重量

        for (int i =0;i<n&&currentWeight<w;i++){
            //尝试添加当前价值最高的礼物
            totalValue+=values[items[i][0]];
            currentWeight+=weights[items[i][0]];
        }
        return totalValue;

        }
    public static void main(String[] args) {
        int[] values = {60, 100, 120}; // 物品价值
        int[] weights = {10, 20, 30};  // 物品重量
        int W = 50; // 背包容量
        int n = values.length; // 物品数量

        System.out.println("The maximum value using Greedy approach is " + knapsackGreedy(W, weights, values, n));
    }
};

1.4、贪心算法的局限性

1. 局部最优而非全局最优。
2. 无法回溯：贪心算法一旦做出了选择，就不会改变了，意味着这个结果是最终的。
3. 忽略以后的可能性，贪心算法在做出选择的时候，没有考虑到对未来选择的影响。在01背包问题中，选择一个物品可能会限制背包未来装载其他物品的能力

让我们举个例子来展示一下贪心算法的局限性：

假设我们有以下物品和背包容量：
- 物品A：重量为10，价值为60
- 物品B：重量为20，价值为100
- 物品C：重量为30，价值为120
- 背包容量：50

使用贪心算法，我们可能会按照单位重量价值排序：
- 物品A：价值/重量 = 60 / 10 = 6
- 物品B：价值/重量 = 100 / 20 = 5
- 物品C：价值/重量 = 120 / 30 = 4

按照贪心算法，我们首先选择的是物品A，因为它的单位重量价值最高。然后我们考虑物品B，背包剩下40的容量，可以继续选择B，最后剩下了20，但是C的重量为30，不能选择，所以最终的价值为60+100=160。

但是最优结果是B+C的价值为220。

像这种对全局，且选择对之后的情况有影响的建议使用动态规划。

2.分治法、

2.1、分治算法策略

分治法采用的是分而治之，各个击破的策略。采用这个方法必须有两个重要的性质：最优子结构和子问题独立。

最优子结构：指一个问题可以分解成若干个规模较小的子问题，各个子问题和原问题类型相同：问题规模缩小到一定程度，就可以直接解决；该问题的解包含着其他的子问题的解，将子问题的解合并最终能够得到原问题的解。

2.2、分治算法和递归

1. 分割
2. 求解
3. 合并

结果 求解问题（问题规模）{
if（问题规模足够小）//边界条件
   求解小规模子问题
else 
    while(存在子问题){
          求解问题（问题规模）;
     return 各子问题合并后的解；
 }

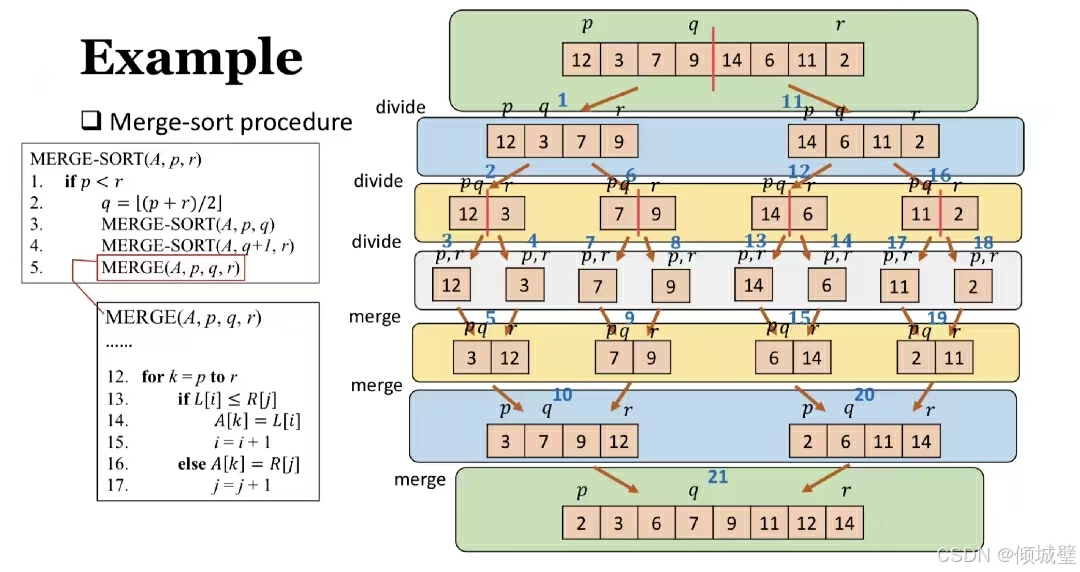
 下面通过解决归并排序的例子，来演示算法过程。

先将数组分成两半，递归对这两半进行排序，然后将排序好的两半合并成一个有序数组。

代码演示：

public class MergeSort {
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            //找到中间索引
            int middle = left + (right - left) / 2;
            //递归调用mergeSort方法，用于将数组分成两个部分
            mergeSort(arr, left, middle);
            mergeSort(arr, middle + 1, right);

            //合并排序好的两半
            merge(arr, left, middle, right);
        }
    }

    private static void merge(int[] arr, int left, int middle, int right) {
        //临时数组存储左右两个部分
        int[] leftTemp = new int[middle - left + 1];
        int[] rightTemp = new int[right - middle];

        //复制数据到临时数组上
        System.arraycopy(arr, left, leftTemp, 0, leftTemp.length);
        System.arraycopy(arr, middle + 1, rightTemp, 0, rightTemp.length);

        //合并临时数组回到原数组arr中
        //初始化三个索引变量
        int leftTempIndex = 0;
        int rightTempIndex = 0;
        //mergeIndex指向数组的起始位置
        int mergeIndex = left;


        while (leftTempIndex < leftTemp.length && rightTempIndex < rightTemp.length) {
            if (leftTemp[leftTempIndex] <= rightTemp[rightTempIndex]) {
                arr[mergeIndex++] = leftTemp[leftTempIndex++];
            } else {
                arr[mergeIndex++] = rightTemp[rightTempIndex++];
            }
        }
        //将剩余的元素复制回原数的arr中
        while (leftTempIndex < leftTemp.length) {
            arr[mergeIndex++] = leftTemp[leftTempIndex++];
        }
        while (rightTempIndex < rightTemp.length) {
            arr[mergeIndex++] = rightTemp[rightTempIndex++];
        }


    }

    public static void main(String[] args) {
        int[] array = {12, 11, 13, 5, 6, 7,2,3,4,5,6,87};
        mergeSort(array, 0, array.length - 1); // 对整个数组进行归并排序

        System.out.println("Sorted array:");
        for (int value : array) {
            System.out.print(value + " ");
        }
    }
}

合并是关键的步骤，下面我来演示代码运行流程帮助理解

假设我们有两个有序子数组：

 左子数组 leftTemp：{1, 3, 5}

 右子数组 rightTemp：{2, 4, 6}

我们的目标是将这两个子数组合并成一个有序数组。合并过程如下：

初始化索引：为两个子数组设置索引，分别指向每个子数组的起始位置。对于 leftTemp 和 rightTemp，索引初始值均为 0。

比较元素：比较两个子数组索引指向的元素。在第一次迭代中，leftTemp[0] 是 1，rightTemp[0] 是 2。

选择较小元素：选择两个元素中较小的一个，并将其复制到结果数组中。在这个例子中，1 小于 2，所以我们将 1 复制到结果数组中。同时，leftTemp 的索引增加 1。

更新索引：更新指向较小元素的子数组的索引。现在，leftTemp 的索引变为 1，指向下一个元素 3。

重复比较：继续比较 leftTemp 和 rightTemp 中索引指向的元素，重复步骤 3 和 4，直到其中一个子数组的所有元素都被复制到结果数组中。

复制剩余元素：如果一个子数组的所有元素都被复制了，但另一个子数组还有剩余元素，将剩余元素直接复制到结果数组的末尾。在这个例子中，当我们复制完 leftTemp 中的所有元素后，rightTemp 中的元素 2 和 4 将直接复制到结果数组的末尾。

完成合并：当两个子数组的所有元素都被复制到结果数组中时，合并操作完成。

3.动态规划

采用动态规划求解问题必须有两个性质：最优子结构和子问题重叠

最优子结构，采用分治法求解，将一个大问题分解成若干个规模较小的子问题，通过合并求解子问题而得到原问题的解。

子问题重叠，采用备忘录求解。“子问题重叠”指分解出的子问题不是相互独立的，有重叠部分。如果采用分治法求解，重叠的子问题将被重复计算多次。

动态规划采用了备忘录解决子问题重叠问题，对于每一个子问题只求解一次，采用备忘录保存每个子问题的计算结果。当我们再次求解某个子问题的时候，只要在备忘录中找结果即可。

下面举个例子就明白了- 青蛙跳阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。

是不是很简单，直接暴力递归

public class RecursiveFrogJump {

    // 递归函数，计算青蛙跳上第 n 级台阶的方法数
    public static int jumpFloor(int n) {
        if (n <= 1) {
            return 1;
        }
        // 递归计算跳上第 n 级台阶的方法数
        return jumpFloor(n - 1) + jumpFloor(n - 2);
    }

    public static void main(String[] args) {
        int stairs = 10; // 10级台阶
        System.out.println("Total ways to jump " + stairs + " stairs: " + jumpFloor(stairs));
    }
}

but，这样子的话会超时！因为会多出很多没必要的重复计算。

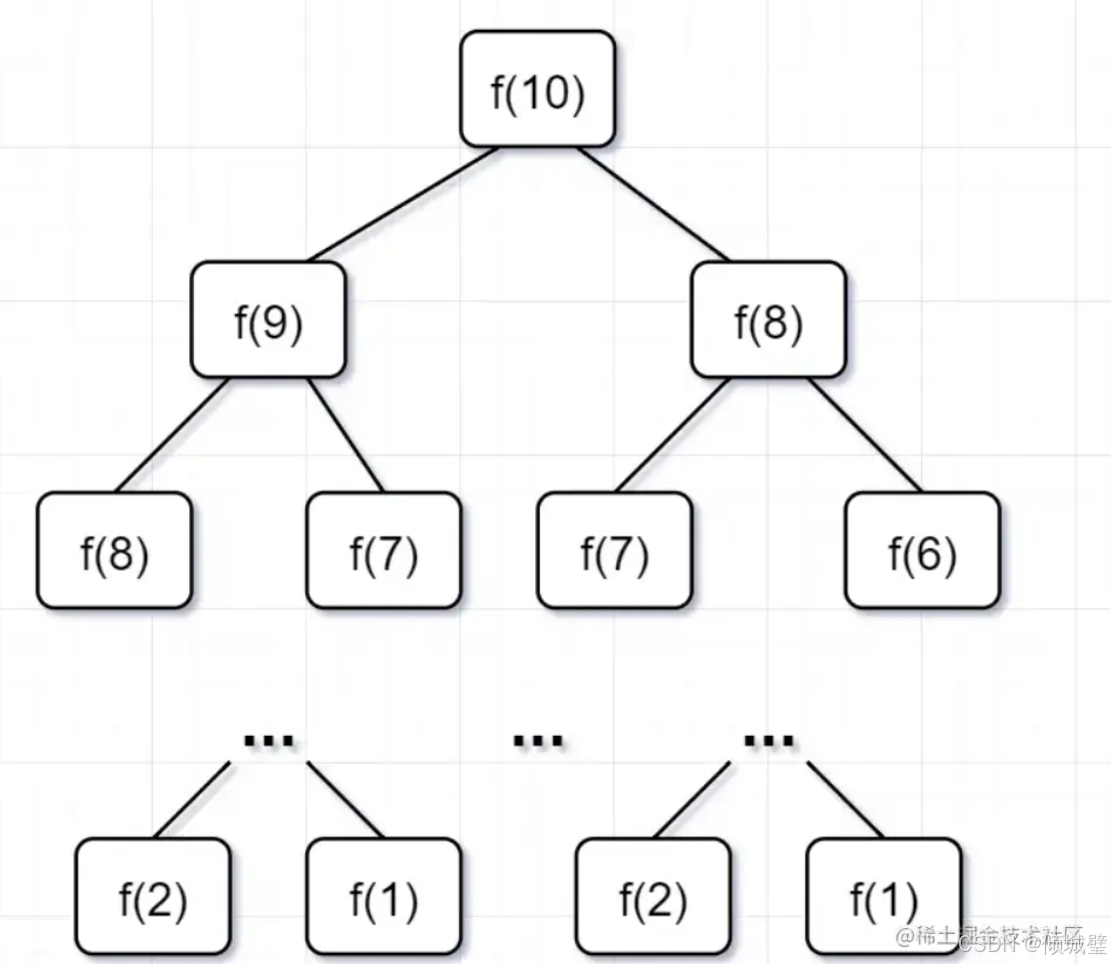
因为递归的本质可以看作是在构建一颗递归树，所以我们通过树来分析一下。

•  根节点：对应于最初的递归调用，即jumpFloor（n）。
• 左子节点：对于递归调用jumpFloor（n-1），表示从当前台阶跳1级
• 右子节点：对于递归调用jumpFloor（n-2），表示从当前台阶跳2级

一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是 O(1)；

问题个数 = 递归树节点的总数，递归树的总节点 = 2^n-1，所以是复杂度O(2^n)。

因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时很正常的了。

回过头来，你仔细观察这颗递归树，你会发现存在大量重复计算，比如f（8）被计算了两次，f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！

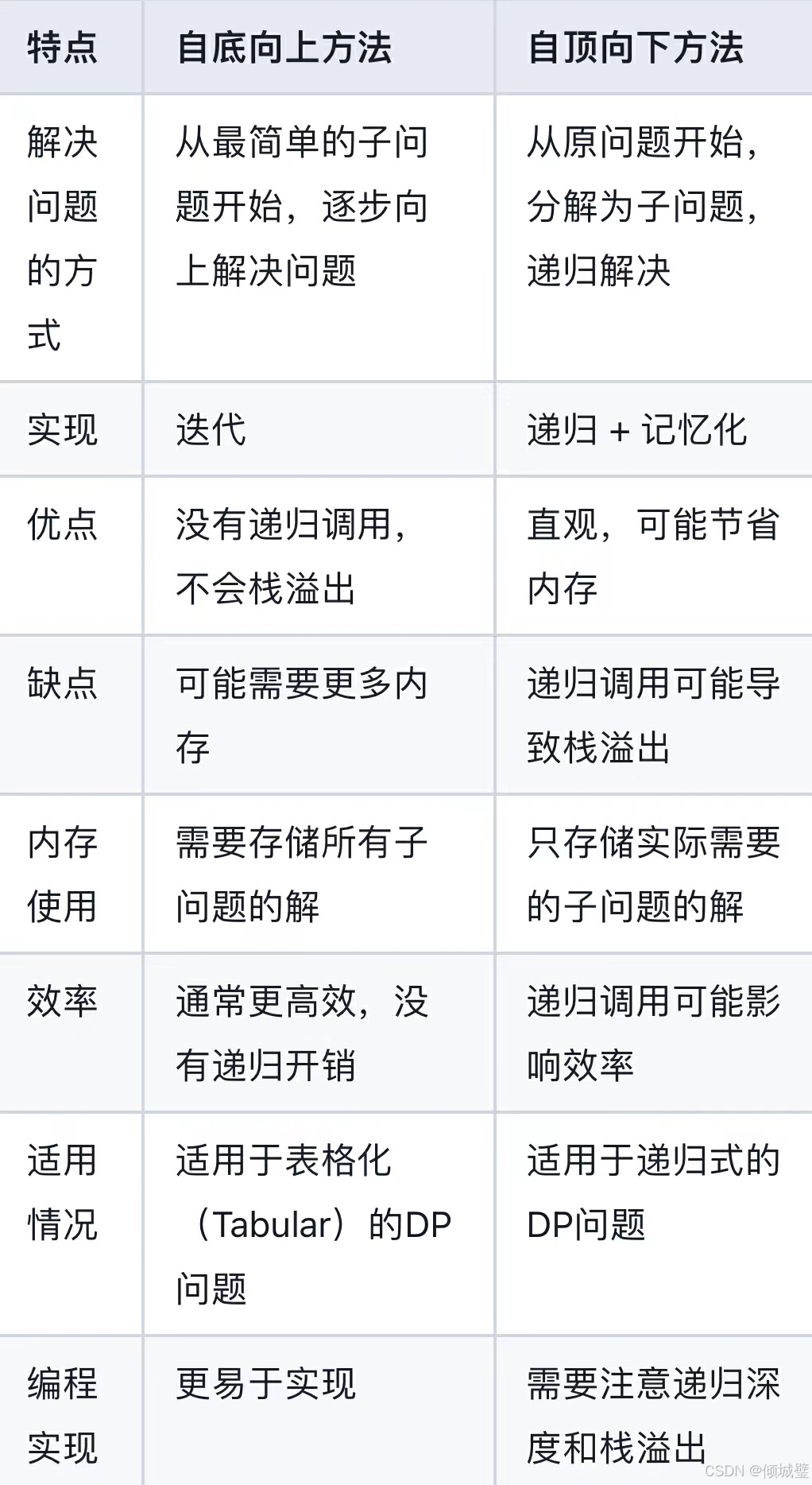
3.1、自顶向下

下面是代码实现：

public class MemoizedFrogJump {

    // 备忘录数组，用于存储已经计算过的台阶数的方法数
    private static int[] memo;

    // 带有备忘录的递归函数
    public static int jumpFloor(int n) {
        if (n <= 1) {
            return 1;
        }
        // 如果已经计算过这个台阶数的方法数，直接从备忘录中返回结果
        if (memo[n] != 0) {
            return memo[n];
        }
        // 否则，递归计算方法数，并存储结果到备忘录中
        memo[n] = jumpFloor(n - 1) + jumpFloor(n - 2);
        return memo[n];
    }

    public static void main(String[] args) {
        int stairs = 10; // 10级台阶
        // 初始化备忘录数组，长度为 stairs + 1，初始值设为 0
        memo = new int[stairs + 1];
        System.out.println("Total ways to jump " + stairs + " stairs: " + jumpFloor(stairs));
    }
}

这个也被称为自顶向下的方法，从问题最初状态开始，逐步的向下分解问题。

特点：

1. 用递归实现
2. 且有备忘录（通常是一个数组或者哈希表）来存储已经计算过的子问题来存储已经计算过的子问题。

3.2、自底向上

现在来介绍自底向下的方法：

从问题的基本情况开始，逐步向上构建问题的解，直到达到目标状态

特点：

迭代实现，通常使用循环结构实现，不需要递归

状态表：使用一个表格（通常是一个数组）来存储状态的解，表格的索引对应于问题的状态

优化点：不需要额外的内存空间来存储备忘录，但是可能需要更多的计算时间来填充整个状态表。

public class BottomUpFrogJump{
    public static int jumpFloorBottomUp(int n){
        if (n<=1){
            return 1;
        }
        int[] dp =new int[n+1];
        dp[0]=1;
        dp[1]=1;
        for (int i =2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

    public static void main(String[] args) {
        int n =10;
        int result =jumpFloorBottomUp(n);
        System.out.println(result);
    }
    
}

在自底向上的迭代方法中：我们定义了一个dp数组，其中dp[i]存储跳上第i级台阶的方法数，我们初始化dp[0]和dp[1]为1，然后通过一个循环，从第二级台阶开始，逐步计算到n级台阶。

3.4自顶向下和自底向上的区别和优缺点

3.3、动态规划解决01背包问题

二维数组解决该问题：

public class Knapsack01 {
    /**
     * @param w 物品的重量
     * @param v 物品的价值
     * @param n 物品的个数
     * @param m 背包的容量
     */
    public static int knapsack1(int[] w, int[] v, int n, int m) {
        int[][] dp = new int[n + 1][m + 1];
        //这里我们是从1开始的，因为0没有任何意义
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                if (w[i - 1] > j)
                    dp[i][j] = dp[i - 1][j];
                else
                    dp[i][j] = Math.max(dp[i - 1][j],
                            v[i - 1] + dp[i - 1][j - w[i - 1]]);
            }
        }
        return dp[n][m];
    }

    public static void main(String[] args) {
       int[] weights ={2,1,3,2};
        int[] values ={12,10,20,15};
        int capacity =5;//背包的容量
        int num =4;
        System.out.println(knapsack1(weights,values,num,capacity));
    }
}

这道题我们的核心思想就是，不同的物品放入背包中，得到的最大价值是多少。

下面是个人理解，可以参考一下：

首先我们动态规划的思想是解决子问题嘛，那么意思就是说在这个问题里面，我们不断的尝试将单个物品放入在允许放入的背包重量范围内，然后将状态记录下来，永远记录的是最大的价值，然后再继续重复操作，在每次将的单个物品放入时，不断的去寻找之前的相应状态下的最大价值再加上现有的价值。

是不是看到很懵啊？没关系呀，理解代码的最好方式不就是摸索代码的运行规律嘛。

这里的难点是在状态转移方程那部分

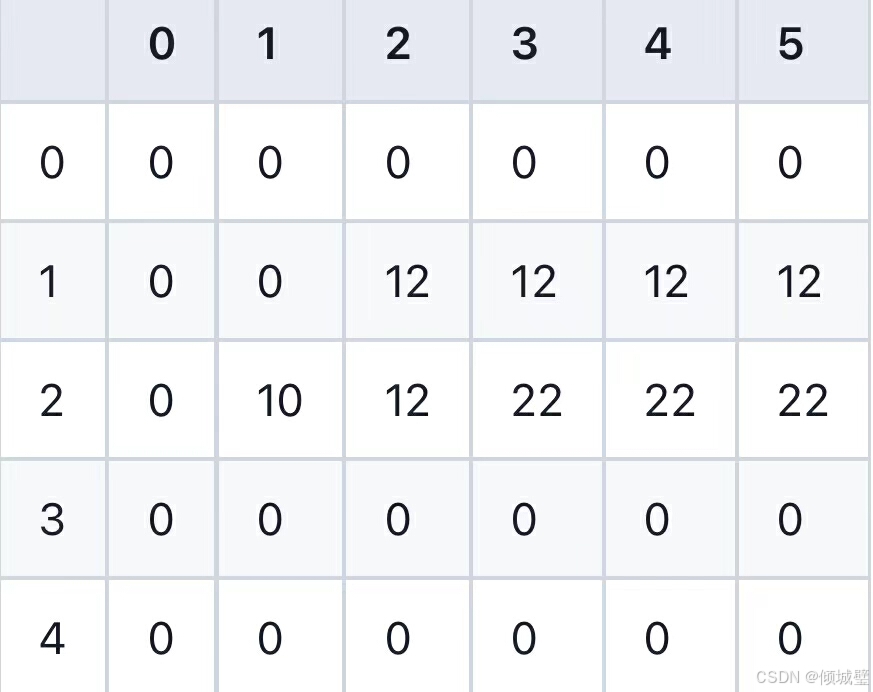
好的，我们现在来重点来看是如何更新dp的

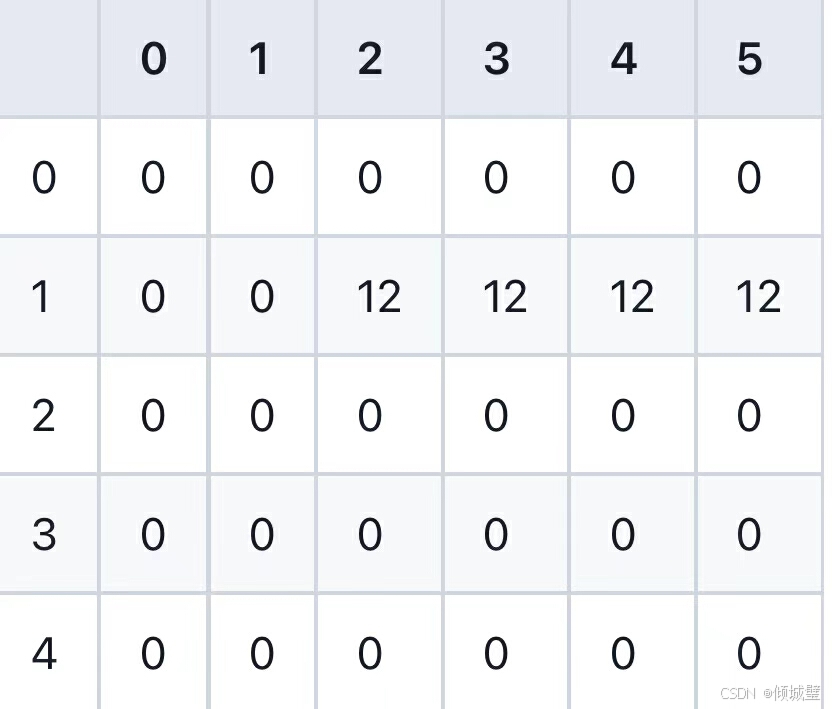
1.对于第一个物品（重量为2，价值为12）；

• 当j<2时，物品重量大于背包容量，不能放入，所以dp[1][j]=dp[0][j]，即0；
• 当j>=2时，物品可以放入背包内，此时dp[1][j]=12+dp[0][j-2];

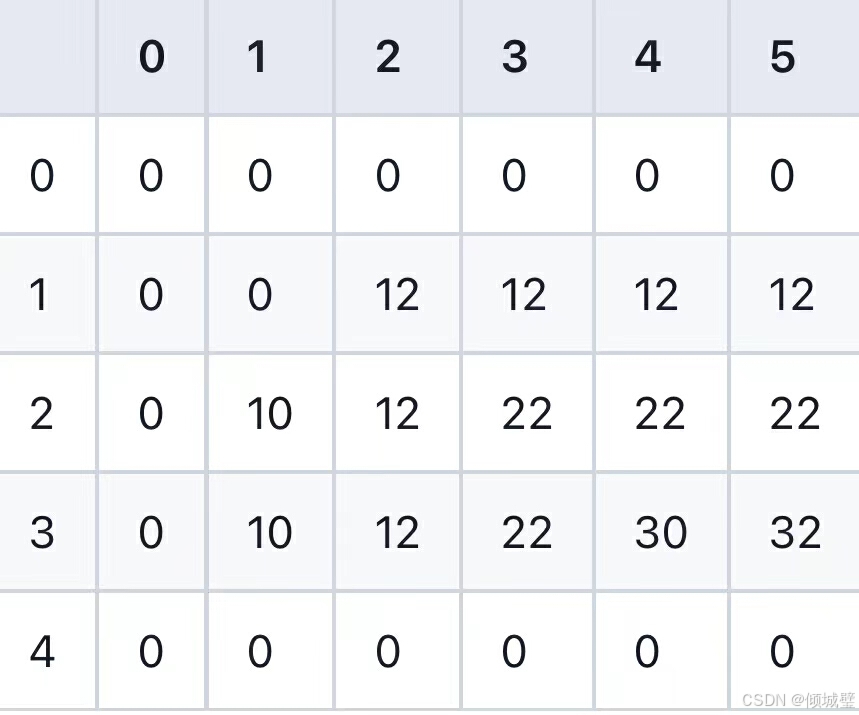
 2.对于第二个物品（重量为1，价值为10）：

• 当j<1时，物品重量大于背包容量，不能放入，所以dp[2][j]=dp[1][j]；
• 当j>=1时，物品可以放入背包内，此时dp[2][j]=Math.max(dp[1][j],10+dp[1][j-1]);

3.对于第三个物品（重量为3，价值为20）： 

• 当j<3时，物品重量大于背包容量，不能放入，所以dp[3][j]=dp[2][j]；
• 当j>=3时，物品可以放入背包内，此时dp[2][j]=Math.max(dp[2][j],20+dp[2][j-3]);

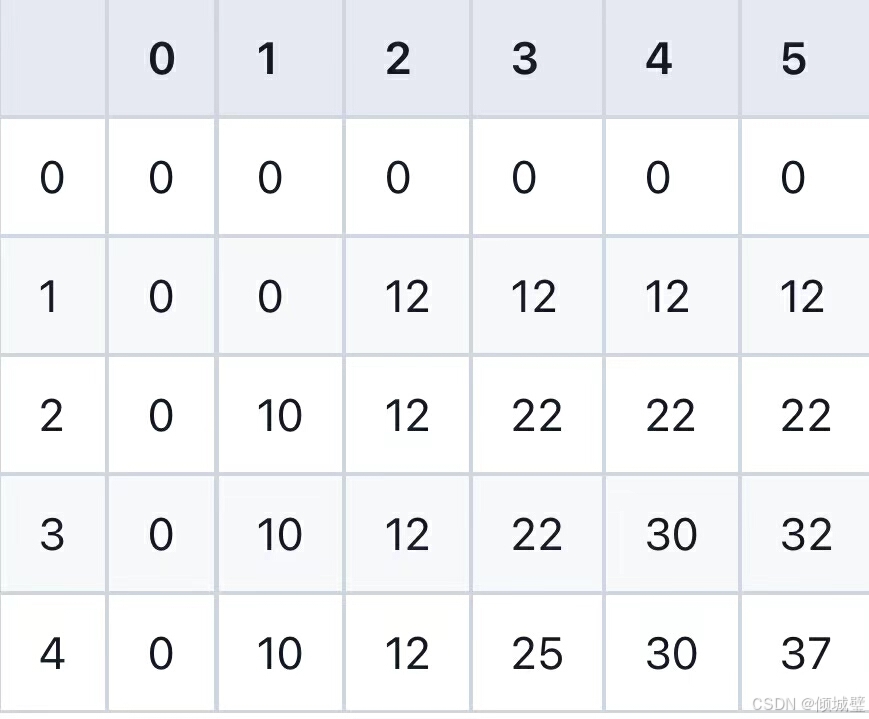
 4.对于第四个物品（重量为2，价值为15）：

• 当j<2时，物品重量大于背包容量，不能放入，所以dp[4][j]=dp[3][j]；
• 当j>=2时，物品可以放入背包内，此时dp[4][j]=Math.max(dp[3][j],15+dp[3][j-2]);

是不是直接woc！大彻大悟了？ 

其实这个问题还能再简化一下，我们其实只要设置一个一维数组的dp就好了。这样子我们可以简化使用的空间，优化了内存！空间复杂度从O(m*n)降到了O（n）

一维数组解决下面是代码实现：

public class Knapsack01 {
    //w是背包的总容量
    //values[i]：物品i的价值
    //weight[i]：物品i的重量
    //n是物品的总数
    public static int knapsack(int w, int[] weights, int[] values, int n) {
        //创建一个数组，长度为背包容量加1
        //这个数组将存储每个容量下在最大价值
        int[] dp = new int[w + 1];
        //遍历所有物品，从第一个物品到第n个物品
        for (int i = 0; i < n; i++) {
            //从小到大遍历背包容量，从当前物品的重量开始
            for (int j = w; j >= weights[i]; j--) {
                //对于每一个物品i，这个循环从背包的总容量w开始递减，直到当前物品的重量weight[i]
                dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);//状态转移方程
            }
        }
        return dp[w];//返回背包容量的w时的最大价值

    }

    public static void main(String[] args) {
        int[] weights ={2,1,3,2};
        int[] values ={12,10,20,15};
        int capacity =5;//背包的容量
        int num =4;
        System.out.println(knapsack1(weights,values,num,capacity));

    }
}

 我们的设计思路是基于动态规划的“滚动数组”技巧，通过我们二维数组对该题目的解法发现，我们每一次只要保存上一行的信息就OK了，所以我们不需要存储整个二维数组，我们只需要一个一维数组就行了，这个一维数组在每次迭代中都会更新，以反应当前行的状态。

接下来我们继续来感受一下一维数组的执行过程：

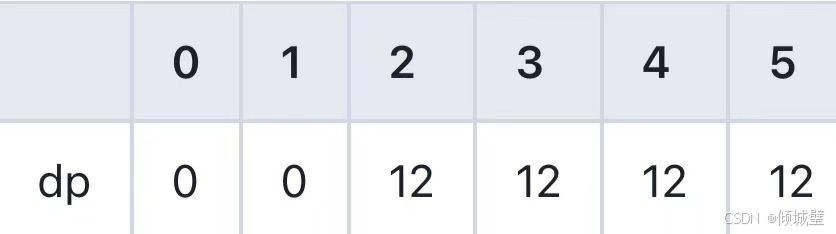
1.对于第一个物品（重量为2，价值为12）：

• 当j<2时，物品重量大于背包容量，不能放入，即0；
• 当j>=2时，物品可以放入背包内，此时dp[j]=Math.max(dp[j],12+dp[j-2]);

 2.对于第二个物品（重量为1，价值为10）：

• 当j<1时，物品重量大于背包容量，不能放入，还是0；
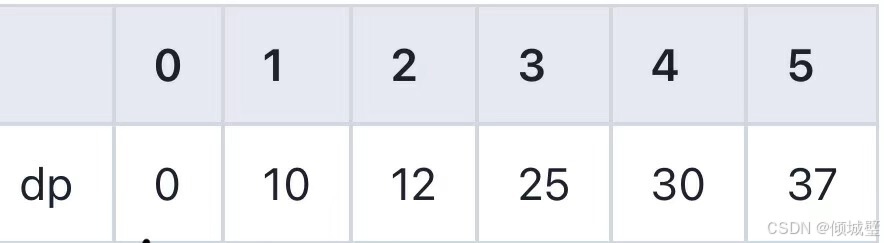
• 当j>=1时，物品可以放入背包内，此时dp[2][j]=Math.max(dp[j],10+dp[j-1]);

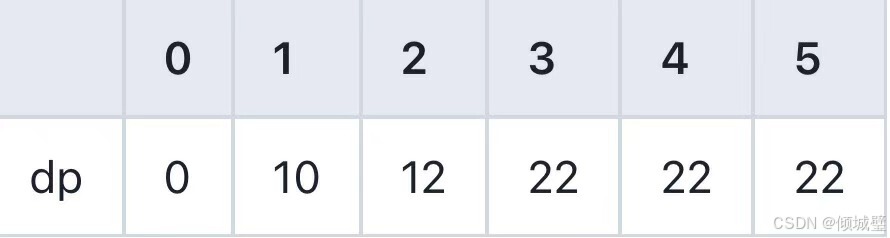
 3.对于第三个物品（重量为3，价值为20）：

• 当j<3时，物品重量大于背包容量，不能放入，依旧保持上一行的dp[j]状态；
• 当j>=3时，物品可以放入背包内，此时dp[j]=Math.max(dp[j],20+dp[j-3]);

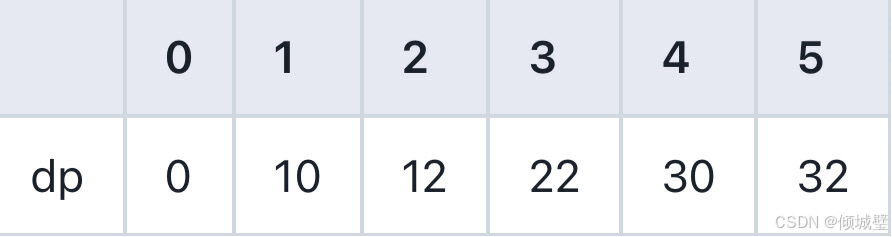
 4.对于第四个物品（重量为2，价值为15）：

• 当j<2时，物品重量大于背包容量，不能放入，所以保持上一行的状态；
• 当j>=2时，物品可以放入背包内，此时dp[4][j]=Math.max(dp[j],15+dp[j-2]);