探秘差分数组：算法星河中闪耀的区间掌控之星

本篇鸡汤：夜深人静，正是你追梦的时刻。熬过这段孤独，未来会因你而闪亮！

~~探索新知，点亮智慧！关注我，一起成长，点赞收藏不迷路！~~

欢迎拜访：羑悻的小杀马特.-CSDN博客

本篇主题：~~带你进入差分数组的世界，探索奥秘~~

制作日期：2025.01.01

隶属专栏：C/C++题海汇总

~~本篇通过差分数组的介绍引入以及配合例题带大家对差分数组有不一样的认识：~~

~~下面我们会对差分数组详细介绍，可以去看看，其实也可以根据例题先来理解这样更方便；博主会在文末放上小总结，欢迎大家来吸取呀！~~

一· 差分数组：

1.1概念：

差分数组是基于一个原始数组构建出来的辅助数组，用于更高效地处理原始数组上的区间修改操作以及后续的查询操作。

其次就是关于差分数组定义：

设原始数组为 nums，长度为 n：

diff[0] = nums[0];

对于 i > 0，diff[i] = nums[i] - nums[i - 1];

下面就举个例子，来介绍一下差分数组是怎么操作的：

例如，给定原始数组 nums = {1, 3, 6, 10}，计算其差分数组 diff 的过程如下：

diff[0] = nums[0] = 1;
diff[1] = nums[1] - nums[0] = 3 - 1 = 2;
diff[2] = nums[2] - nums[1] = 6 - 3 = 3;
diff[3] = nums[3] - nums[2] = 10 - 6 = 4;

所以差分数组 diff = {1, 2, 3, 4}。

1.2区间更新操作：

1.2.1基本原理：

当需要对原始数组 nums 的区间 [left, right]（left 和 right 为区间的左右边界索引，索引从 0 开始）进行统一的增量操作（比如每个元素都加上值 val）时，利用差分数组可以高效地完成更新，只需执行 diff[left] += val 和 diff[right + 1] -= val（需确保 right + 1 在差分数组合法索引范围内，若 right + 1 >= n 则不用执行后面这一步）操作即可，这样就能在 o(1) 时间复杂度内完成区间更新，相较于直接在原始数组上遍历更新（时间复杂度为 o(len)，len 为区间长度）效率大大提升。

1.2.2代码实现区间更新操作：

// 对差分数组进行区间更新操作
void updateDiff(vector<int>& diff, int left, int right, int val) {
    diff[left] += val;
    int n = diff.size();
    if (right + 1 < n) {
        diff[right + 1] -= val;
    }
}

代码解释说明：
假设我们有上述的差分数组 diff = {1, 2, 3, 4}，现在要对原始数组对应的区间 [1, 2] 内的元素都加上 2。

调用 updateDiff(diff, 1, 2, 2)：，执行以下操作：

首先执行 diff[1] += 2，此时 diff 变为 {1, 4, 3, 4}。

然后因为 right + 1 = 3 小于 diff 的大小（4），所以执行 diff[3] -= 2，

最终 diff 变为 {1, 4, 3, 2}。

1.3还原原始数组：

1.3.1基本原理：

可以通过差分数组 diff 还原出原始数组 nums，计算方式为：

nums[0] = diff[0];

对于 i > 0，nums[i] = nums[i - 1] + diff[i];

1.3.2代码实现：

// 根据差分数组还原原始数组
vector<int> getOriginalArray(vector<int>& diff) {
    int n = diff.size();
    vector<int> nums(n);
    nums[0] = diff[0];
    for (int i = 1; i < n; ++i) {
        nums[i] = nums[i - 1] + diff[i];
    }
    return nums;
}

代码解释说明：

对于更新后的差分数组 diff = {1, 4, 3, 2}，还原原始数组的过程如下：
nums[0] = diff[0] = 1;
nums[1] = nums[0] + diff[1] = 1 + 4 = 5;
nums[2] = nums[1] + diff[2] = 5 + 3 = 8;
nums[3] = nums[2] + diff[3] = 8 + 2 = 10;
所以还原后的原始数组 nums = {1, 5, 8, 10}。

1.4简单小应用：

下面来模拟对一组数据（比如可以想象成学生成绩数组等情况）进行区间更新后查看更新结果的场景：

#include <iostream>
#include <vector>
using namespace std;

// 对差分数组进行区间更新操作
void updateDiff(vector<int>& diff, int left, int right, int val) {
    diff[left] += val;
    int n = diff.size();
    if (right + 1 < n) {
        diff[right + 1] -= val;
    }
}

// 根据差分数组还原原始数组
vector<int> getOriginalArray(vector<int>& diff) {
    int n = diff.size();
    vector<int> nums(n);
    nums[0] = diff[0];
    for (int i = 1; i < n; ++i) {
        nums[i] = nums[i - 1] + diff[i];
    }
    return nums;
}

int main() {
    // 模拟原始数组（比如学生成绩数组）
    vector<int> nums = {85, 90, 92, 94};
    int n = nums.size();

    // 构建差分数组
    vector<int> diff(n);
    diff[0] = nums[0];
    for (int i = 1; i < n; ++i) {
        diff[i] = nums[i] - nums[i - 1];
    }

    // 对区间 [1, 2] 的数据进行更新，比如成绩都加5分
    updateDiff(diff, 1, 2, 5);

    // 还原更新后的原始数组
    vector<int> updatedNums = getOriginalArray(diff);

    cout << "原始数组: ";
    for (int num : nums) {
        cout << num << " ";
    }
    cout << endl;

    cout << "更新后的数组: ";
    for (int num : updatedNums) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

对上述代码来解释一下：

①首先定义了原始数组 nums 模拟学生成绩情况。

②然后构建了对应的差分数组 diff。

③接着对成绩数组的区间 [1, 2] 内的成绩进行加分操作（这里加 5 分），通过调用 updateDiff 函数利用差分数组高效完成更新。

④最后通过 getOriginalArray 函数还原出更新后的成绩数组 updatedNums，并输出原始数组和更新后的数组进行对比，可以看到区间内的数据按照要求进行了相应的更新变化。

小结：差分数组在处理这类需要频繁进行区间更新以及后续可能查询原始数组元素情况的场景中，能有效地降低时间复杂度，提升程序运行效率。

这里我们也许会说，差分数组一定是万能的嘛？肯定不是，下面我们展开优缺点来谈谈：

二·差分数组优缺点：

2.1优点：

2.1.1高效的区间更新操作：

当需要对原始数组的某个区间进行相同的更新操作（如增减一个固定值）时，差分数组展现出了卓越的时间效率。例如，对原始数组nums的区间[left, right]的每个元素加上值val，直接操作原始数组需要遍历区间内的每个元素，时间复杂度为o(right-left+1)。

而使用差分数组，只需进行两次操作：diff[left]+=val和diff[right + 1]-=val（假设right + 1不超出数组范围），时间复杂度为o(1)。

下面我们举个例子：

例如，有一个长度为 1000 的数组，要对区间[100, 500]内的元素都加上 10。如果直接更新原始数组，需要进行 401 次加法运算。而使用差分数组，只需两次操作就能记录下这个更新意图，后续可以根据差分数组快速还原更新后的原始数组。

2.1.2便于记录变化过程：

差分数组可以清晰地记录原始数组每个位置的变化量。通过观察差分数组，能够直观地了解原始数组在哪些位置发生了变化以及变化的幅度。

例如，在一个记录股票价格每日波动的数组中，差分数组可以很好地体现每天价格是上涨还是下跌以及涨跌的幅度。如果差分数组的某个元素为正，说明原始数组对应的位置价格上涨；为负则表示价格下跌；为 0 表示价格不变。

2.1.3支持动态更新和查询：

在面对一系列动态的区间更新操作后，仍然能够相对高效地查询原始数组任意位置的值。可以通过前缀和的方式，预先处理差分数组，使得查询原始数组某一位置的值的时间复杂度降低到o(1)。

例如，在一个实时资源分配系统中，资源数量数组需要频繁地在某些区间内增加或减少资源。通过差分数组记录变化，并且预先计算好前缀和，就可以快速查询任意时刻某个资源点的实际资源数量。

2.2缺点：

2.2.1空间开销：

需要额外的空间来存储差分数组。如果原始数组规模很大，差分数组的空间占用可能会成为一个问题。尤其是在内存资源有限的情况下，这种额外的空间开销可能会对系统性能产生一定的影响。

例如，对于一个包含 1 亿个元素的原始数组，就需要额外开辟 1 亿个元素的空间来存储差分数组，这可能会占用大量内存。

2.2.2理解和实现的复杂性：

相较于直接对原始数组进行操作，差分数组的概念和操作逻辑相对复杂。对于初学者来说，理解差分数组的原理（如如何构建、如何进行区间更新、如何还原原始数组）以及正确地实现相关操作（如边界条件的处理）需要花费一定的时间和精力。

例如，在更新差分数组的区间操作时，需要正确处理区间的左右边界，特别是右边界的更新操作（diff[right + 1]-=val）容易被忽略或者处理错误，导致还原后的原始数组不符合预期。

2.2.3应用场景的局限性：

差分数组主要适用于区间更新频繁且需要查询更新后数组元素的场景。如果只是偶尔进行单点更新或者不需要查询更新后的数组，使用差分数组可能会增加不必要的复杂性和空间开销。

例如，如果只是简单地修改原始数组中的一个元素，直接操作原始数组会更简单直接，使用差分数组反而会使代码变得复杂。

2.3.差分数组具体应用场景：

2.3.1区间统计问题：

在数据统计领域，差分数组常用于处理区间统计问题。

例如，在统计一段时期内的销售数据变化情况时，原始数组记录每天的销售额，差分数组可以用于记录每天销售额的增减量。如果要统计某一区间内销售额的总增长量，通过差分数组可以很方便地计算出来。

即：假设原始数组nums记录了一家商店连续 10 天的销售额，现在要统计第 3 天到第 7 天销售额的总增长量。通过差分数组，可以快速计算出这个区间内的增长量，而不需要逐个累加原始数组中每天的销售额。

2.3.2数组区间更新场景：

在很多算法问题和实际应用中，经常会遇到对数组进行区间更新的情况。

如在图像像素处理中，对图像的某个矩形区域内的像素进行统一的亮度调整或者颜色通道值的修改。可以将图像的像素值存储在一个数组中，通过差分数组来高效地完成区间更新操作。

举个例子吧：

例如，在一个灰度图像中，像素值数组存储了每个像素的灰度值。如果要对图像中间的一个矩形区域内的像素灰度值都增加 50，使用差分数组可以快速地记录这个更新操作，并且在需要时还原出更新后的像素值数组。

2.3.3动态规划中的状态转移优化：

在动态规划问题中，有些状态转移方程涉及到区间的更新和查询。差分数组可以作为一种优化手段，减少状态转移过程中的计算量。

例如，在计算最长上升子序列的变种问题，其中涉及到对某个区间内的子序列长度进行统一更新的情况时，差分数组可以帮助优化计算过程。

为什么呢可以这样优化呢？

假设在一个动态规划算法中，需要频繁更新某个区间内的状态值，并且后续要根据这些状态值计算最终结果。使用差分数组可以在更新状态时降低时间复杂度，从而提高整个动态规划算法的效率。

三·差分数组例题引入：

3.1题目介入：

下面我们将根据一道蓝桥杯的题目，来应用我们上面所述，毕竟能实践才能决定知识是否是你的：

原题链接：小明的彩灯

3.2题目分析：

3.2.1题目简述：

首先，题意对于我们来说应该是不难理解的；每次给出的分别是左右区间，以及要加的值；我们只需要根据区间去进行相应操作就行；但是，最后不是直接把原数组返回，要注意到：

其次我们还要看到数据范围（也因此我们使用了long long而不是int）：

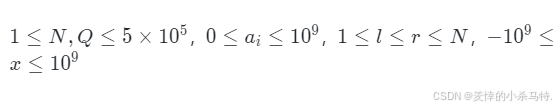
也就是我们操作完后；如果原数组值变成了负数就要把它改成0；下面我们不采用暴力去模拟破解它；而是采用差分数组的思路解决：

3.2.2 差分数组使用：

上面我们不是介绍了差分数组；下面我们就此题而应用（也就是分为下面几步）：

①差分数组填充：

我们这里对于差分数组是多开了两个空间：因为：其一，就是让区间端值和下标一一对应；其二，就是在更新差分数组的时候可能出现越界（ diff[end + 1] -= val）；

  vector<ll>diff(N + 2);//差分数组

下面我们定义：

diff[i]表示原数组第i个位置比i-1个位置的值大多少

填充：

  for (int i = 1; i <= N; i++) {
        cin >> v[i];
        diff[i] = v[i] - v[i - 1];//虚拟节点（v[0]，只是在差分数组，以及还原原数组有用）
    }

②多次操作：

 vector<pair<pair<ll, ll>, ll>> oper(Q + 1);//存储每组操作变量
    for (int i = 1; i <= Q; i++) cin >> oper[i].first.first >> oper[i].first.second >> oper[i].second;

    int j = 1;
    //根据每次操作及时更新原数组对应的差分数组：
    while (Q--) {
        ll start = oper[j].first.first, end = oper[j].first.second, val = oper[j].second;
        diff[start] += val;
        diff[end + 1] -= val;//这里注意越界；如果是最后一个下标则可能越界，故差分数组要再多开一个
        j++;
    }

③原数组更新并完成打印操作：

 for (int i = 1; i <= N; i++)v[i] = v[i - 1] + diff[i];//数次操作后根据差分数组还原原数组
    v.erase(v.begin());//删除虚拟节点
    for (auto a : v) {
        ll t = a >= 0 ? a : 0;//由题意知，负数为0
        cout << t << " ";
    }

3.2.3小tips：

~~下面博主为大家分享此题的几个小细节处理：~~

①就是数据问题，一定要long long。

②就是多开一个空间，让区间端值对应；方便后序操作。

③就是差分数组填充是常用的一定要保证空间足够，否则就要进行判断防止如果右区间恰好是原数组尺寸所导致的越界发生；因此至少比原数组多开两个最多搞成最大值。

④ 就是在打印的时候不能变更新（当发现是负数就变成0，然后再更新后面的值，因为原数组最终的值是严格遵循与差分数组的，这样就相当于改变了固有的条件）比如下面错误代码：

 /* for (int i = 1; i <= N; i++) {
        v[i] = (v[i-1] + diff[i]) >= 0 ? v[i-1] + diff[i] : 0;
        cout << v[i] << " ";
    }*/

这是不可取的；因此注意好这几点就没多大问题了。

四·差分数组总结：

其实看了上面一大堆理论分析介绍，不一定能懂，下面我们就通俗一点：

4.1什么样的情景应用：当发现同时对一块区间进行多次操作，且每次操作对当前区间每个值的影响是相同的，而且范围又不是特别大（对空间要求不高）此时就可以应用。

4.2怎么用：①首先，先求出原数组最开始的差分数组，

②再之，根据多少次进行对差分数组操作（而不是原数组），

③最后，根据操作完差分数组的值来重获最终数组（此时有了最终的差分数组就不需要原数组了，也可以说原数组的作用就在于填充一开始的差分数组，接着我们只需要利用类似动态规划dp填表的顺序恢复最终数组即可）

~~本篇完结，希望对你学习差分数组有帮助感谢支持！！！~~