第一章 序章

1.1 前言

• KMP算法并不好理解，读者尽量选择一个完整的时间阅读本文并最好准备一张草稿纸可以自我进行适当演算笔画，能显著加快理解速度。
• 本文尽可能直观地去描述两种模式匹配算法的规则与过程，对于算法的学习，读者应该在脑中构建一个数据结构的动态空间，在读思想的同时组织并操作这个空间中的数据。
• 算法需要理解，需要一定的记忆，但一定不可以直接背代码或思想描述，效率很低且容易养成不爱思考的坏习惯。💪
• 此外，一般而言看一遍就掌握KMP算法是不太可能的，不明白的时候一定要反复去看，千万别把时间浪费在找攻略上了😂。

1.2 前置约定

• S和T是两个给定的串；
• S称为主串；
• T称为模式串；
• 模式匹配：在串S中找到等于T的子串的过程，如果找到则匹配成功，否则匹配失败；
• 迭代器指针：并不是语法意义上的指针，而是一个逻辑意义上的指针，语法上是一个常数变量，用于遍历串；
• 主串匹配串：主串的某一子串，表示当前正在被匹配；
• 前缀：一个串中一定包含第一个元素的子串；如“abc”的前缀有"a"、“ab”、“abc”；
• 后缀：一个串中一定包含最后一个元素的子串；如"abc"的后缀有"c"、“bc”、“abc”；
• 子模式串：模式串的一个子串；
• 数组的0号位用于存储串长，即元素从1号位开始存

第二章 BF匹配算法

全称是Brute-Force，也称为简单匹配方法。从名字就可以看出它很简单吧😄，是一个很原始的穷举方法。

2.1 算法思路

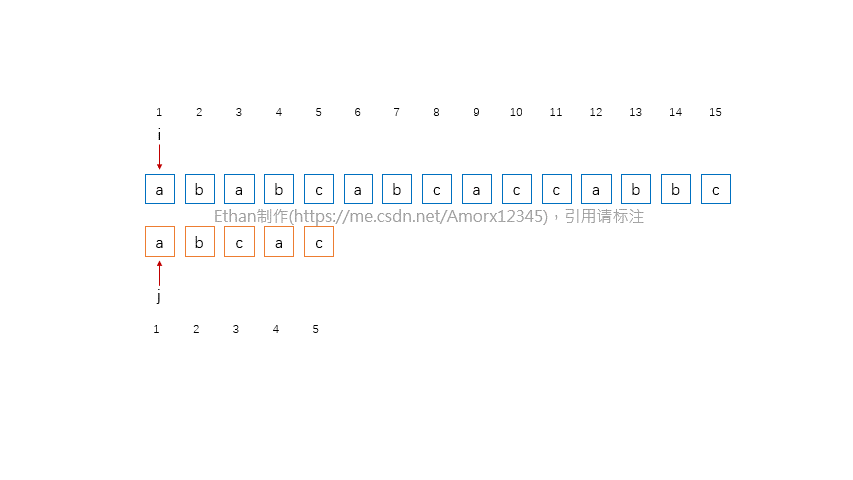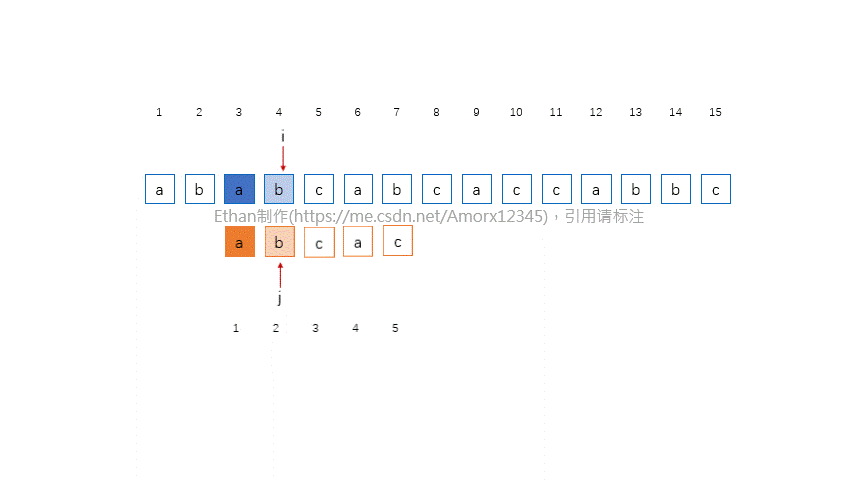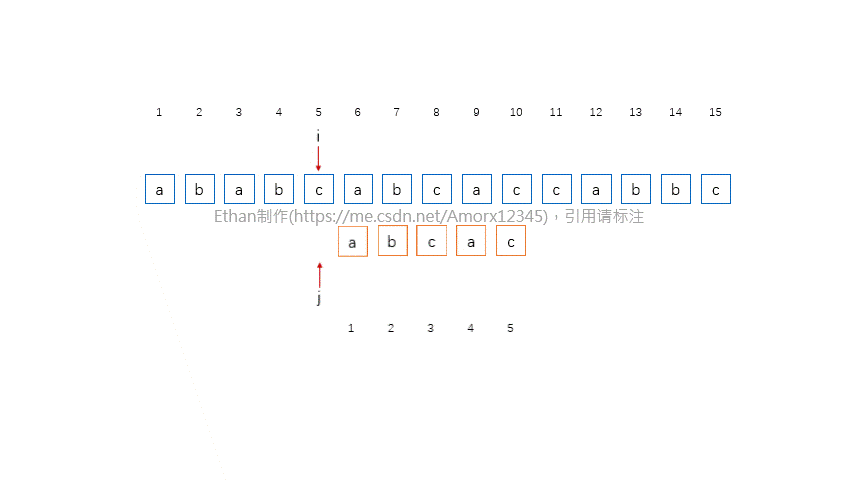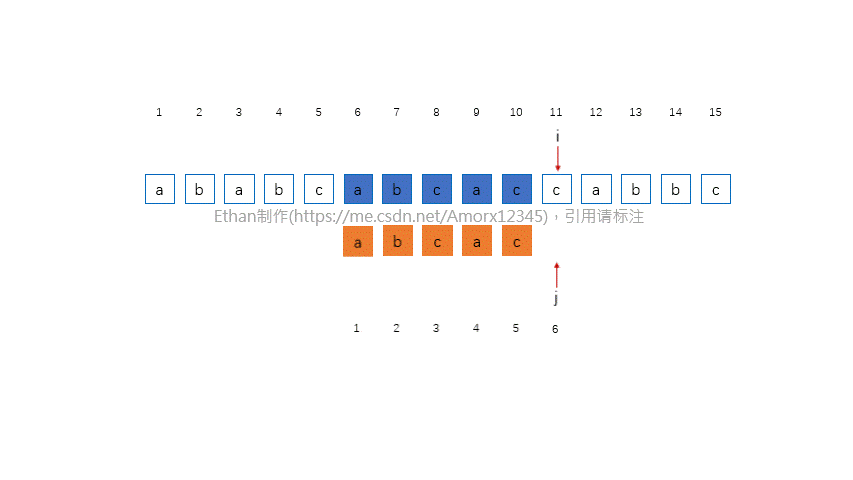
从主串S的第一个字符开始，与模式串T中的第一个字符进行比较，若相等，则继续逐个比较后续字符；否则从主串S的第二个字符开始重新与模式串T的第一个字符进行比较。依次类推，若主串S的第i个字符开始，每个字符依次和模式串T中的对应字符相等，则匹配成功，返回i；否则，匹配失败，返回-1。

2.2 示意动画

看完示意动画，应该已经大致明白了一个算法的工作流程，这里主要工作有：

• 主串和模式串迭代器指针的移动
• 两指针所指元素的匹配比较
• 两迭代器指针的回溯

2.3 代码

int index(sstring s, sstring t, int pos) {
   
    int i = pos, j = 1;
    while (i<=s[0]&&j<=t[0]) {
   
        if (s[i]==t[j]) {
   
            i++;
            j++;
        } else {
   
            i = i - j + 2;