接着上一篇的文章继续对电子技术进行探讨,上一篇把基本的数学知识介绍了一下,重点关注电工电路中的系统的频率响应,可以看做是开环系统,而没有涉及到闭环系统。而本篇我们就讨论在电子设计中的闭环系统,尤其是关于系统稳定性的知识,虽然稳定性问题我们之前有所提及,这里我们对其进行更深入的认知,并探讨如何保证系统的稳定性,避免自激振荡的出现。然后以放大器作为具体的设计实例,探讨如何进行放大器的设计。
文章目录
1.闭环系统分析基础
1.1什么是反馈
在《模拟电子技术基础》中,有这么一段话:反馈是指将电路中输出电量的一部分货全部通过反馈网络,用一定的方式送回到输入回路,以影响输入、输出电量的过程。
具体什么是反馈,我想只要是在这个领域摸爬滚打的人,都应该对反馈有所认知。
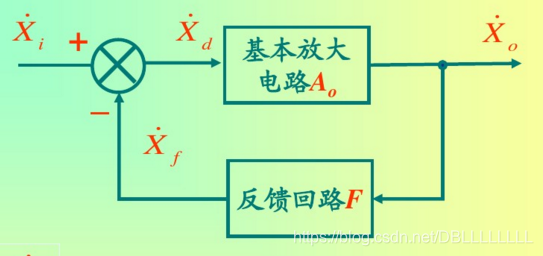
如下图所示是十分常见的反馈的模型。这里我们需要确定一些比较重要的参数:
1.误差放大器环节:它接收信号
x
d
x_d
xd,并产生输出信号
x
o
x_o
xo,且有以下关系:
x
o
=
A
x
d
x_o=Ax_d
xo=Axd
其中,
A
A
A为该放大器的正向增益,也称为该电路的开环增益。
2.反馈网络:该网络对
x
o
x_o
xo采样,并产生反馈信号
x
f
x_f
xf,且有以下关系:
x
f
=
F
x
o
x_f=Fx_o
xf=Fxo
其中F为该反馈网络的增益,称为该电路的反馈系数。有些时候也用
β
\beta
β来表示,称为反馈因子,实际上都是一个东西。
3.求和网络,用
Σ
\Sigma
Σ来表示,它产生差值信号:
x
d
=
x
i
−
x
f
x_d=x_i-x_f
xd=xi−xf
其中,由于差值信号是通过两个信号量相减得到的,因此我们称之为负反馈,可以看出,如果系统是负反馈,则
x
i
x_i
xi和
x
f
x_f
xf应该是同号的。
4.一个闭环系统总是由上面三个部分构成,如果我们把
x
i
x_i
xi看做输入,
x
o
x_o
xo看做输出,其他的变量视为中间变量,那么我们可以得到整个系统的输入和输出之间的关系:
A
f
=
x
o
x
i
=
A
1
+
A
F
A_f=\frac{x_o}{x_i}=\frac{A}{1+AF}
Af=xixo=1+AFA
这里
A
f
A_f
Af称为电路的闭环增益。
可以看出因为系统为负反馈,因此
x
i
x_i
xi和
x
f
x_f
xf同号,因此AF>0,1+AF>1,因此
A
f
A_f
Af<A。这里1+AF就被称为反馈量,或者叫反馈深度。
5.如果我们把环路断开,让信号沿着放大器、反馈网络、求和器,那么信号经历的总增益为-AF,该增益的负值称为环路增益:
T
=
A
F
T=AF
T=AF
6.通过环路增益,我们可以把电路的闭环增益写成:
A
f
=
1
F
×
T
1
+
T
A_f=\frac{1}{F}×\frac{T}{1+T}
Af=F1×1+TT,当
T
=
∞
T=\infty
T=∞时,理想闭环增益为:
A
i
d
e
a
l
=
lim
T
−
∞
A
f
=
1
F
A_{ideal}=\lim_{T-\infty}A_f=\frac{1}{F}
Aideal=T−∞limAf=F1
A
i
d
e
a
l
A_{ideal}
Aideal被称为理想闭环增益。
这里我们对负反馈中的各个增益名称进行了说明,后面我们会经常反复的提及上述名词,因此对于这些名词我们一定要牢记在心。
总结一下:
A
A
A为开环增益
F为反馈系数
A
f
A_f
Af为闭环增益
1+AF为反馈深度
T
=
A
F
T=AF
T=AF为环路增益
A
i
d
e
a
l
=
1
F
A_{ideal}=\frac{1}{F}
Aideal=F1为理想闭环增益
1.2反馈电路的分类
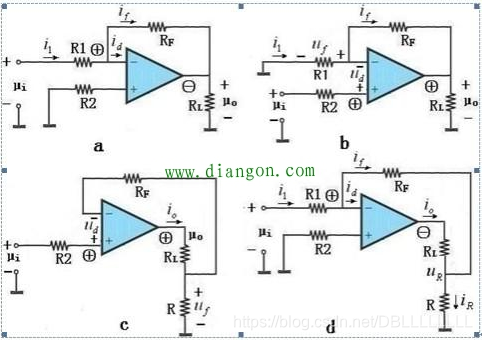
运算放大器的反馈电路有以下四种基本的拓扑模型:
电压串联、电压并联、电流串联、电流并联
看起来很复杂,其实分开来说,是电压/电流和串联/并联的组合,那么我们在分类的时候其实是可以分开判断的。
1.串联反馈和并联反馈
一句话概括,串联并联看输入,输入信号和反馈信号在不同极的是串联,输入信号和反馈信号在同极的是并联。
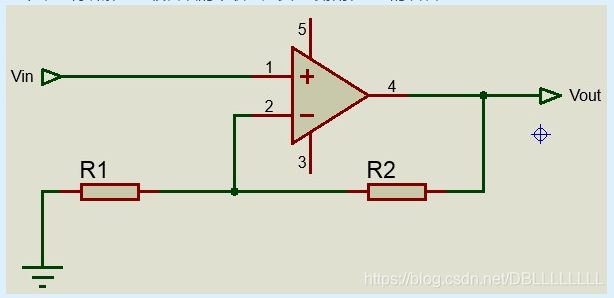
该图为串联反馈,可以看到,输入信号和反馈信号不同极。
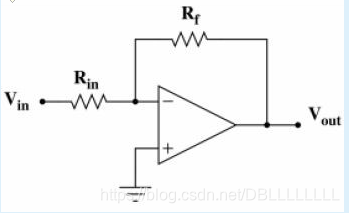
该图为并联反馈,可以看到,输入信号和反馈信号同极。
2.电压反馈和电流反馈
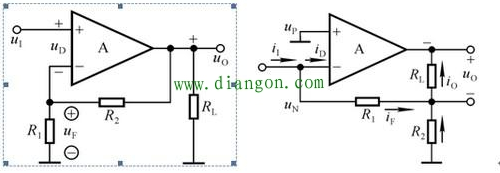
一句话概括,电压电流看输出,反馈如在负载前为电压反馈,反馈如在负载后为电流反馈。
如上图,左边反馈网络取的信号是在负载之前,为电压信号。右图反馈网络取的信号是在负载之后,为电流信号,因此左边为电压反馈,右边为电流反馈。
那么我们给出典型的四种拓扑形式的负反馈电路。
左上为电压并联负反馈,右上为电压串联负反馈,左下为电流并联负反馈,右下为电流串联负反馈。
现在我们已经能够判断一个放大器电路的反馈种类了。不过可能有些人会有个疑问,为什么我们要判断放大器电路的种类?
这是因为,我们在上一节讨论反馈的各个参数的时候,使用的变量其实是x,这是因为我们不确定具体的电路中,这个x到底代指的是电流还是电压。而通过上述的分类,我们可以知道,如果是串联反馈,表明加法器中的x为电压,如果是并联反馈,表明加法器中的x为电流。如果是电压反馈,表明反馈网络中的输入为电压,如果是电流反馈,表明反馈网络中的输入为电流。
这样,通过确定一个电路的拓扑类型,我们就能确定上述反馈方程中各个变量在具体电路中的含义,才能对一个实际的电路进行分析。
例如:对于电压串联反馈,由于是串联反馈,因此加法器中的参数为电压,有:
v
d
=
v
i
−
v
f
v_d=v_i-v_f
vd=vi−vf
又因为是电压反馈,所以反馈网络的采样信号为电压信号,有:
v
f
=
F
v
o
v_f=Fv_o
vf=Fvo
这样,我们知道了,对于电压串联反馈,其反馈方程为:
v
d
=
v
i
−
v
f
v_d=v_i-v_f
vd=vi−vf
v
f
=
F
v
o
v_f=Fv_o
vf=Fvo
同理可得:
电压并联反馈: i d = i i − i f i_d=i_i-i_f id=ii−if i f = F v o i_f=Fv_o if=Fvo
电流串联反馈: v d = v i − v f v_d=v_i-v_f vd=vi−vf v f = F i o v_f=Fi_o vf=Fio
电流并联反馈: i d = i i − i f i_d=i_i-i_f id=ii−if i f = F i o i_f=Fi_o if=Fio
这样我们在分析不同拓扑的电路的时候, 就注意应该采用基尔霍夫电压定律还是电流定律,应该把反馈网络看成跨阻的还是正常的。
1.3环路增益的求法
到现在为止,我们已经知道了反馈电路中各个参数的定义,也能对实际的电路进行分类,并根据分类的结果写出该电路的反馈方程式。下面我们需要做的,就是对方程式中各个参数进行具体的求值。
其中由于环路增益T在反馈理论中起着核心作用,所以我们这里主要说明的是环路增益的求法。在求环路增益之前,我们先说,为什么环路增益在反馈理论中起了核心作用。
首先是因为,环路增益越大,闭环增益越接近理想值。
通过之前的说明,我们知道了,闭环增益的方程为:
A
f
=
A
1
+
A
F
A_f=\frac{A}{1+AF}
Af=1+AFA
理想闭环增益为:
A
i
d
e
a
l
=
1
F
A_{ideal}=\frac{1}{F}
Aideal=F1
二者之间的关系可以写成:
A
f
=
A
i
d
e
a
l
×
T
1
+
T
=
A
i
d
e
a
l
×
(
1
−
1
1
+
T
)
A_f=A_{ideal}×\frac{T}{1+T}=A_{ideal}×(1-\frac{1}{1+T})
Af=Aideal×1+TT=Aideal×(1−1+T1)
可以看出,若环路增益T越大,闭环增益的大小约接近于理想闭环增益,我们就越能忽略其开环增益A,而只需要关注反馈网络F。
此外,T的大小还决定了电路是否稳定,我们在后面的内容会讲解到。
总而言之,环路增益T的求取十分关键,那么对于一个实际的复杂的电路,我们如何求得其环路增益呢?
这里介绍一种方法,也是在放大器电路分析中常用的方法,就是先求反馈系数F(有些书本写作 β \beta β),然后根据开环增益A,求环路增益:T=AF
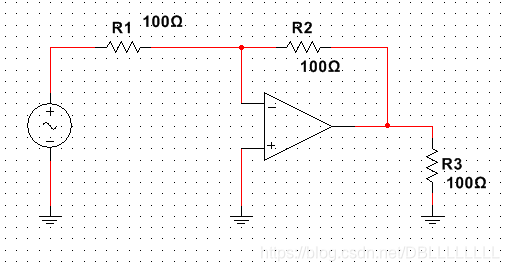
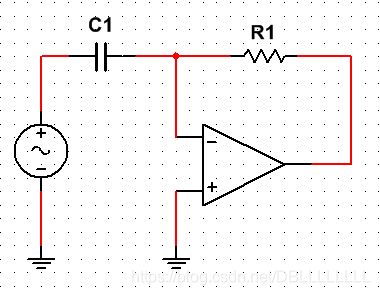
举例来说,对于下图的放大器电路:
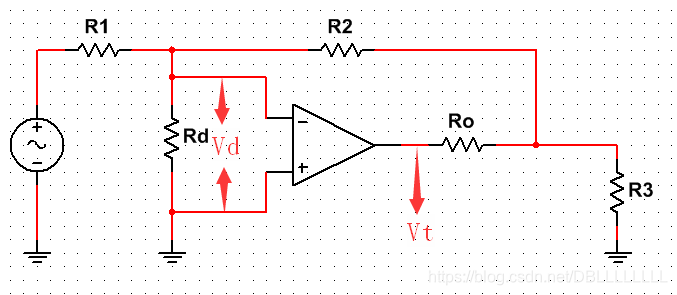
如果考虑实际的放大器电路,需要在该电路的基础上进行一些改动,增加输入电阻 r d r_d rd和输出电阻 r o r_o ro。
实际电路模型为:
该电路的反馈系数有以下公式:
F
=
−
v
d
v
t
∣
x
i
=
0
F=-\frac{v_d}{v_t}|_{x_i=0}
F=−vtvd∣xi=0
那么我们可以看到,
v
d
v_d
vd是由
v
t
v_t
vt两次分压得到的,即:
v
d
=
−
1
×
R
1
∣
∣
R
d
R
1
∣
∣
R
d
+
R
2
×
(
R
1
∣
∣
R
d
+
R
2
)
∣
∣
R
L
(
R
1
∣
∣
R
d
+
R
2
)
∣
∣
R
L
+
R
o
×
v
t
v_d=-1×\frac{R_1||R_d}{R_1||R_d+R_2}×\frac{(R_1||R_d+R_2)||R_L}{(R_1||R_d+R_2)||R_L+R_o}×v_t
vd=−1×R1∣∣Rd+R2R1∣∣Rd×(R1∣∣Rd+R2)∣∣RL+Ro(R1∣∣Rd+R2)∣∣RL×vt
(这里的-1是因为上面的 v d v_d vd是以放大器的正极为正,放大器的负极为负,因此相对于 v t v_t vt反了一次相)
所以:
F
=
−
v
d
v
t
∣
x
i
=
0
=
R
1
∣
∣
R
d
R
1
∣
∣
R
d
+
R
2
×
(
R
1
∣
∣
R
d
+
R
2
)
∣
∣
R
L
(
R
1
∣
∣
R
d
+
R
2
)
∣
∣
R
L
+
R
o
F=-\frac{v_d}{v_t}|_{x_i=0}=\frac{R_1||R_d}{R_1||R_d+R_2}×\frac{(R_1||R_d+R_2)||R_L}{(R_1||R_d+R_2)||R_L+R_o}
F=−vtvd∣xi=0=R1∣∣Rd+R2R1∣∣Rd×(R1∣∣Rd+R2)∣∣RL+Ro(R1∣∣Rd+R2)∣∣RL
对该式子进行化简得:
F
=
1
1
+
R
2
/
R
1
+
R
2
/
R
d
×
1
(
1
+
R
o
/
(
(
R
1
∣
∣
R
d
+
R
2
)
∣
∣
R
L
)
F=\frac{1}{1+R_2/R_1+R_2/R_d}×\frac{1}{(1+R_o/((R_1||R_d+R_2)||R_L)}
F=1+R2/R1+R2/Rd1×(1+Ro/((R1∣∣Rd+R2)∣∣RL)1
通过这个式子我们就得到了一个实际电路的反馈系数F,如果我们将该实际电路当做理想放大器来处理,则输入电阻无穷大,输出电阻为零。那么该反馈系数F就变为:
F
=
1
1
+
R
2
/
R
1
=
R
1
R
1
+
R
2
F=\frac{1}{1+R_2/R_1}=\frac{R_1}{R_1+R_2}
F=1+R2/R11=R1+R2R1
可以看出,这个反馈系数在电路中就是反馈网络的分压的公式。
在根据已知的开环增益A(该数值一般都由厂家给出),我们就能得到环路增益T。
因此要求环路增益,就要先求反馈系数F。
2.运算放大器的静态限制问题
在运算放大器的使用中,我们注意到,随着频率或增益的增加,放大器电路可能就慢慢的偏离我们所设计的性能。总结来说,这种性能的降低,主要有静态限制和动态限制两个问题。首先我们先来探讨一下静态问题。
所谓静态问题,是指,即使我们将工作频率保持在一个相对较低的水平,此时仍然有一些限制会影响到运算放大器的性能,这种限制就是静态限制。
比较常见的有:输入偏置电流 I B I_B IB、输入失调电流 I O S I_{OS} IOS、输入失调电压 V O S V_{OS} VOS、交流噪声密度 e n e_n en和 i n i_n in,以及需要考虑的一些问题包括热漂移TC( V O S V_{OS} VOS)、共模抑制比CMRR、馈电抑制比PSRR、增益非线性度等。
下面我们分别对这些问题进行一个说明。
2.1输入偏置电流和输入失调电流
定义:
实际运放的两个输入端并不是绝对的高阻,这就造成实际上的运算放大器是有电流流入的。假设对于运放来说,两个极流入(流出)的电流大小为
I
P
、
I
N
I_P、I_N
IP、IN,这里这两个值没有方向,只关注大小。
这两个值的均值为输入偏置电流:
I
B
=
I
P
+
I
N
2
I_B=\frac{I_P+I_N}{2}
IB=2IP+IN
这两个值的差值为输入失调电流:
I
O
S
=
I
P
−
I
N
I_{OS}=I_P-I_N
IOS=IP−IN
范围:
一般来说,输入失调电流要小于输入偏置电流,一般来说,常见的运算放大器,其输入偏置电流和输入失调电流的范围从 1 0 − 15 A 到 1 0 − 4 A 10^{-15}A到10^{-4}A 10−15A到10−4A之间,常见的数值一般为nA级。
影响:
输入失调电流和输入偏置电流主要影响的是信号的信噪比,这里我们把输入偏置电流等造成的影响视为噪声,关于其计算,我们将在下一节专门进行讲解。
对策:
要解决输入偏置电流的问题,一般来说没有特别有效的方法,只能通过选择低输入偏置电流的运算放大器来解决。
2.2输入失调电压
输入失调电压定义:
在运放开环使用时,加载在两个输入端之间的直流电压 V O S V_{OS} VOS,使得放大器的直流输出为0。
理解:
对于任何一个放大器,即使我们将它的两个输入端都接地,其输出也不为零。此时我们在正输入端加上一个可调电压,通过调整电压,最终使放大器的输出为0,这个电压值的负值就是输入失调电压。它可以看成放大器的正输入端在进入放大器前,串联了一个电压源,导致即使正输入端接地,进入到放大器后的电压也不为零。
范围:
最好的能达到1uV以下,比较好的能达到100uV以下,最大的能达到几十mV。
影响:
如果我们的放大器的闭环电压增益为 A F A_F AF,当放大器输入为零时,输出存在一个等于 A F V O S A_FV_{OS} AFVOS的直流电平,此输出被称为输出失调电压。闭环增益越大,则输出失调电压越大。
对策:如果我们的放大器主要关注的是电平的直流成分,那我们就必须选择输入失调电压远小于输入直流量的放大器,或者通过运放的调零措施来消除这个影响。如果我们仅仅关注被测信号中的交流成分,我们可以在输入和输出端增加交流耦合电路,来消除输入失调电压的影响。
2.3输入失调电压漂移
输入失调电压漂移:
定义:
当温度变化、时间推移、供电电压等环境变化时,输入失调电压会发生变化。
影响:
当我们在使用运算放大器时,即使我们之前已经做好了调零,把运算放大器本身具有的输入失调电压的影响给去除了,但是随着时间的推移,或者如果周围环境温度发生变化等因素,运算放大器又会产生新的输入失调电压。
对策:
首先我们在选型的时候尽量选择漂移系数比较小的运放。其次,有些运放具有自归零技术。
2.4共模抑制比
定义:
运放的差模电压增益与共模电压增益的比值,单位为dB。
C
M
R
R
=
20
log
A
d
A
c
CMRR=20\log\frac{A_d}{A_c}
CMRR=20logAcAd
理解:
我们之前认为,运算放大器电路只对输入之间的电压差进行放大,但是实际上运算放大器对于共模输入电压也是敏感的,只是这个敏感的程度比较小。那么假设对差模电压的增益为
A
d
A_d
Ad,对共模电压的增益为
A
c
A_c
Ac,那么有,总的输出电压为:
v
o
=
A
d
(
v
P
−
v
N
)
+
A
c
(
v
P
+
v
N
2
)
=
A
d
(
v
P
−
v
N
)
+
A
c
v
C
M
v_o=A_d(v_P-v_N)+A_c(\frac{v_P+v_N}{2})=A_d(v_P-v_N)+A_c v_{CM}
vo=Ad(vP−vN)+Ac(2vP+vN)=Ad(vP−vN)+AcvCM
这里,带入上述共模抑制比的概念,我们可以得到:
v
o
=
A
d
[
v
P
−
v
N
+
v
C
M
C
M
R
R
]
v_o=A_d[v_P-v_N+\frac{v_{CM}}{CMRR}]
vo=Ad[vP−vN+CMRRvCM]
可以看出, v C M C M R R \frac{v_{CM}}{CMRR} CMRRvCM的共同作用,相当于在差模电压的基础上由增加了一个电压,这个和我们之前所说的输入失调电压的作用效果是相似的,因此我们可以将系数 1 C M R R \frac{1}{CMRR} CMRR1解释为,当共模电压每增加1V,所产生的输入失调电压的变化率。
范围:
共模抑制比带来的问题,典型值有90dB,相当于31.6uV/V的变化率。较差的70dB,相当于316uV/V的变化率。较好的110dB,相当于3.16uV/V的变化率。
影响:
通过上面的分析,我们可以把共模抑制比的影响看做等效于新增加的输入失调电压来分析。
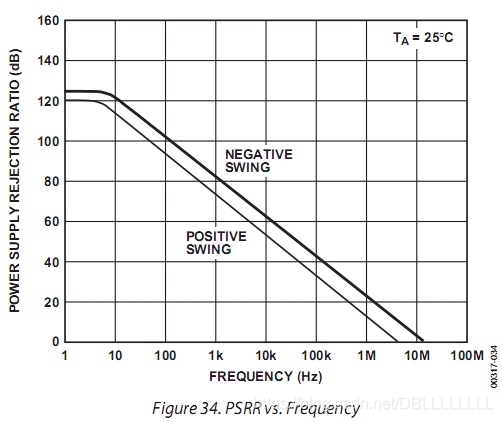
2.5电源抑制比
定义:供电电源的微小变化,也会对输出电压产生影响。与差模抑制比类似,如果我们把这种影响转移到输入端,相当于输入端电压的改变值,这种关系用电源抑制比来表示。
1 P S R R = △ V O S △ V S \frac{1}{PSRR}=\frac{△V_{OS}}{△V_S} PSRR1=△VS△VOS
表示,电源每1V的变化带来的相当于输入偏置电流电压的变化。
范围:
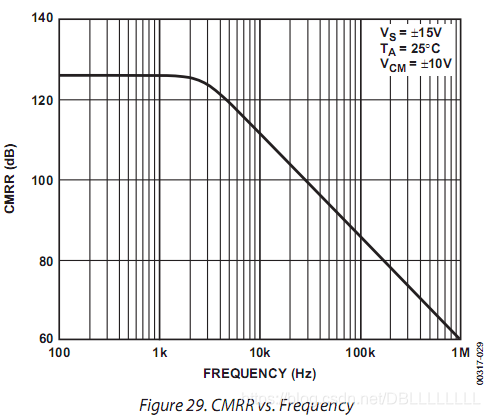
类似上面共模抑制比的范围。但是值得注意的是,许多运算放大器的正负电源的电源抑制比并不相同。且共模抑制比随着频率的变化而变化,一般来说,频率越高,共模抑制比越小。因此在对运算放大器供电时,需要对电源的高频成分进行一个滤除。
影响:
输入偏置电压类似。
对策:
选择高电源抑制比的运算放大器,对运算放大器的电源电路进行合理的滤波。关于电路滤波,可以参考上一篇的内容。
2.6小结
总的来说,我们所谈论的这些问题,其实主要关注的就是输入失调电流、输入偏置电流和输入失调电压,其他的问题或多或少都可以向上面三个问题转化。而我们关注这些量值,除了有利于我们进行选型以外,还有一个十分重要的方面,就是涉及到电路噪声的估计和计算。关于运算放大器噪声的问题,我们将在下一篇文章中重点介绍。
这里先抛去上述的静态限制,我们先来关注一个运放的设计和动态响应。也就是下面的内容。
3.运算放大器的动态限制问题
实际上的运算放大器,只能对一定频率内的信号提供一个较高的增益,对于超过该频率的信号,运算放大器的增益会随着信号频率的增加而减小。且运算放大器的输出和输入之间存在延时。这些问题都是运算放大器对于动态的信号所存在的一些使用上的限制问题。本节内容就重点关注这些问题。
包括:单位增益频率 f t f_t ft,增益带宽乘积GBP,闭环带宽 f B f_B fB,全功率带宽FPB,上升时间 t R t_R tR,转换速率SR和建立时间 t s t_s ts。
3.1开环响应与频率
回到我们之前所时候的运算放大器的设计问题。
我们知道了运算放大器的环路增益T=AF,F的求法我们之前已经说明了,那么剩下的就是运算放大器的开环响应A。
运算放大器的开环响应A往往由厂家提供,现实中的开环响应是与频率有关的,一般来说,在一定频率范围内,开环响应能够保持一个较大的常数,但是随着频率的增加,开环响应可能会随之减小。一般常见的开环响应是主极点响应,它的频谱主要受一个极点控制,由厂家实现,将其他的极点放在了单位增益以下,这样就可以忽略其他的极点的影响。
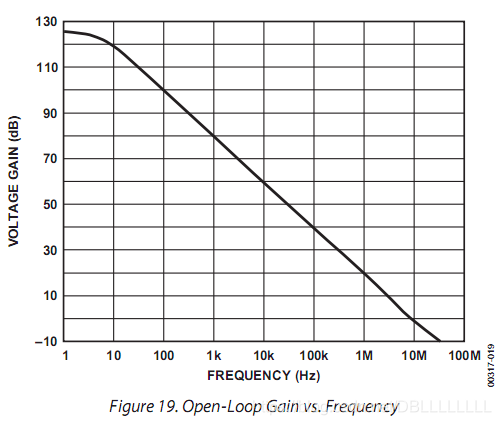
主极点响应使得运算放大器的开环增益类似一个RC低通滤波器,在低频段增益为 a 0 a_0 a0,在频率 f b f_b fb处开始滚降。这个滚降处的频率就是主极点频率。下图可以发现,这个频率大概为5Hz。
通过之前我们所说的系统的频率响应表达式,这里我们可以将下图近似表达为:
A ( j f ) = a 0 1 + j ( f / f b ) A(jf)=\frac{a_0}{1+j(f/f_b)} A(jf)=1+j(f/fb)a0
这里 a 0 a_0 a0为开环直流增益, f b f_b fb是开环-3dB频率,也称为开环带宽。
图中我们可以发现,当增益为1时,开环频率响应的频率为单位增益频率,用 f t f_t ft表示。该图中 f t f_t ft约为8MHz。
我们知道,当滚降的斜率为-20dB/dec时,相当于频率每增大十倍,增益增益减小十倍。那么在该线性区域内,频率和增益的乘积将会是一个常数。这个常数就叫做增益带宽积GBW。
理论上来说,增益带宽积相当于当增益为单位增益时的频率,即上述的单位增益频率,也相当于在开环带宽下的增益。如下图的运算放大器,我们查表可以得到其GBW为8MHz,而其表格中没有给出 f t f_t ft。
3.2环路增益T在动态响应中的分析方法
T=AF,到这里,我们已经得到了A在动态响应中的伯德图。
对于反馈系数F,通过我们之间的分析,结合上一篇对于系统的分析,我们很容易也能想到,F也是一个和频率有关的系统性能,因此我们也可以得到F的伯德图。
已知两者的动态响应,我们如何进行运算,来得到环路增益T的伯德图呢?
我们让 T = A 1 / F T=\frac{A}{1/F} T=1/FA
通过伯德图表示,我们知道,
20
log
T
=
20
log
A
−
20
log
1
F
20\log T=20\log A - 20\log \frac{1}{F}
20logT=20logA−20logF1
这样我们就可以先得到开环增益A和反馈因子 1 F \frac{1}{F} F1的伯德图,再将两个Bode图相减,就得到了环路增益T的Bode图。
这种分析方法是分析放大器动态响应常用的方法,这里一定要充分理解。
3.3闭环响应与频率
开环响应依赖于频率变化而变化,同样的,闭环响应也是如此。
对于同相放大器来说,闭环响应为:
A
f
(
j
f
)
=
A
(
j
f
)
1
+
A
(
j
f
)
F
A_f(jf)=\frac{A(jf)}{1+A(jf)F}
Af(jf)=1+A(jf)FA(jf)
且我们已知了该放大器的开环响应和反馈系数:
A
(
j
f
)
=
a
0
1
+
j
(
f
/
f
b
)
A(jf)=\frac{a_0}{1+j(f/f_b)}
A(jf)=1+j(f/fb)a0
F = R 1 R 1 + R 2 F=\frac{R_1}{R_1+R_2} F=R1+R2R1
代入上式化简可以得到:
A
f
(
j
f
)
=
a
0
(
R
2
+
R
1
)
a
0
R
1
+
R
1
+
R
2
×
1
1
+
j
(
f
/
(
f
b
(
1
+
a
0
R
1
R
1
+
R
2
)
)
)
A_f(jf)=\frac{a_0(R_2+R_1)}{a_0R_1+R_1+R_2}×\frac{1}{1+j(f/(f_b(1+a_0\frac{R_1}{R_1+R_2})))}
Af(jf)=a0R1+R1+R2a0(R2+R1)×1+j(f/(fb(1+a0R1+R2R1)))1
这里我们令:
A
0
=
a
0
(
R
2
+
R
1
)
a
0
R
1
+
R
1
+
R
2
A_0=\frac{a_0(R_2+R_1)}{a_0R_1+R_1+R_2}
A0=a0R1+R1+R2a0(R2+R1)
f B = f b ( 1 + a 0 R 1 R 1 + R 2 ) f_B=f_b(1+a_0\frac{R_1}{R_1+R_2}) fB=fb(1+a0R1+R2R1)
则原式可以写为:
A
f
(
j
f
)
=
A
0
×
1
1
+
j
(
f
/
f
B
)
A_f(jf)=A_0×\frac{1}{1+j(f/f_B)}
Af(jf)=A0×1+j(f/fB)1
可以看出,同相放大器的闭环响应的方程式和开环响应的方程式在形式上是一致的,都是一个低通滤波器的形式,只是直流增益 A 0 A_0 A0和闭环带宽 f B f_B fB不同。
那么闭环增益中直流增益 A 0 A_0 A0和闭环带宽 f B f_B fB具体是多少呢?
对于闭环直流增益
A
0
A_0
A0,当开环直流增益
a
0
a_0
a0无限大时,有
A
0
=
a
0
(
R
2
+
R
1
)
a
0
R
1
+
R
1
+
R
2
=
R
1
+
R
2
R
1
=
1
F
A_0=\frac{a_0(R_2+R_1)}{a_0R_1+R_1+R_2}=\frac{R_1+R_2}{R_1}=\frac{1}{F}
A0=a0R1+R1+R2a0(R2+R1)=R1R1+R2=F1
可以看出,闭环直流增益的大小为1/F,这与我们之前在直流条件下求出来的结果是一样的,分母中忽略的项也就是我们之前所述的增益误差。
而闭环带宽
f
B
f_B
fB则为闭环直流增益
A
0
A_0
A0和开环增益的交点频率。
f
B
=
f
b
(
1
+
a
0
F
)
=
F
f
t
f_B=f_b(1+a_0F)=Ff_t
fB=fb(1+a0F)=Fft
可以看出,引入负反馈之后,增益下降,但是带宽增加。
对于反向放大器来说,其闭环增益类似的进行分析,仍可以得到以下公式:
A
f
(
j
f
)
=
A
0
×
1
1
+
j
(
f
/
f
B
)
A_f(jf)=A_0×\frac{1}{1+j(f/f_B)}
Af(jf)=A0×1+j(f/fB)1
但是这里的
A
0
A_0
A0和
f
B
f_B
fB有所不同:
A
0
=
−
R
2
R
1
;
f
B
=
F
f
t
A_0=-\frac{R_2}{R_1};f_B=Ff_t
A0=−R1R2;fB=Fft
可以看出,转折频率没变,但是直流增益减少,因此反相放大器的图形就像是同相放大器向下平移一段距离。
3.4压摆率和全功率带宽
对于运算放大器来说,如果输入是一个阶跃信号,则输出需要过一段时间才能跟随输出。这意味着,运算放大器的输出和输入之间是存在一个延时的。
如果阶跃输入大于某个数值时,放大器的输出就按照某个固定斜率的直线上升到该电压,这个斜率就是我们所说的压摆率(转换速率)SR。它表明,该运算放大器能够实现的最大的变化速率,单位一般为伏特每微秒V/us。
下图为某运算放大器的SR,典型值为2.8V/us,也就是说,如果放大器需要跟随一个14V的输出,需要5us。
对于正弦信号,我们知道,正弦信号的频率越大,信号变化的速率越大,正弦信号的幅值越大,信号变化的速率越大。那么正弦信号的频率和幅值与压摆率的关系是什么呢?
f V o m < S R 2 π fV_{om}<\frac{SR}{2\pi} fVom<2πSR
只要满足该频率信号的幅值和频率的乘积小于压摆率除以2π,该正弦信号就不会失真。
由此引出一个叫全功率带宽FPB的定义,如果运算放大器产生具有最大可能幅度的不失真交流输出时的最大频率。一般来说,最大可能幅度为供电电压,因此FPB有:
F
P
B
=
S
R
2
π
V
s
a
t
FPB=\frac{SR}{2\pi V_{sat}}
FPB=2πVsatSR
4.运算放大器的稳定性问题
我们在之前已经对放大器的静态和动态问题进行了讨论。看似我们已经可以通过设计来实现一个负反馈放大器了(通过合理的选择开环增益A和反馈系数F)。但是我们通过上一篇的学习知道,负反馈中存在着稳定性问题,当电路存在着振荡的可能,该电路就无法实现正常的运行。因此我们在设计一个能够正常运行的放大器时,放大器的稳定性问题是一定要考虑到的。
4.1稳定性的传统判据
关于反馈电路的稳定性问题,我们在上一篇中已经介绍过了。
简单理解,当某一频率的信号经过各个环节反馈到输入信号时,变成了正反馈,且最终信号的增益大于1时,该信号就会被不断放大,从而产生振荡。因此在相位差达到-180°时,系统此时的增益倍数小于1,则不会振荡,且该分贝数的倒数为增益裕度,意味着此时系统还可以将增益增大多少倍而不至于产生振荡。
另一种理解方法是,当系统的增益倍数为1时,系统的相位距离-180°的角度,称为相位裕度 ϕ m \phi_m ϕm。
如何判断系统的稳定性,就通过上面两个方法来判断。具体更详细的解释,请参考上一篇文章的讲述。
这里再提以下峰值和振铃与相位裕度的关系。
我们通过之前的学习知道,对于二阶系统来说,如果阻比系数太小或者品质因数太大,都会引起峰值GP和振铃OS的现象,这种现象一般来说是不利于信号的传输的。
通过二阶系统的分析,我们发现,尖峰现象和振铃现象存在着一定的关系,如下:
ϕ
m
=
60
°
时
,
G
P
=
0.3
d
B
,
O
S
=
8.8
%
\phi_m=60°时,GP=0.3dB,OS=8.8 \%
ϕm=60°时,GP=0.3dB,OS=8.8%
ϕ m = 45 ° 时 , G P = 2.4 d B , O S = 23 % \phi_m=45°时,GP=2.4dB,OS=23 \% ϕm=45°时,GP=2.4dB,OS=23%
可以看出,相位裕度越小,峰值和振铃现象越严重,因此一般来说,我们希望相位裕度越大越好。
4.2通过截止速率来判断稳定性
通过传统的稳定性判据,我们需要同时得到系统的幅频特性和相频特性。但是在实际设计中,我们往往只关注幅频特性,因为相频特性的叠加较为麻烦,如果没有计算机帮助,我们很难精确的同时画出系统的幅频特性和相频特性并进行对应的稳定性判断。
于是这里我们介绍一种在运放稳定性判断中十分常用的一种方法,那就是截止速率判断方法。
这里就用到了我们上一节所说的,环路增益T在动态响应中的分析方法。
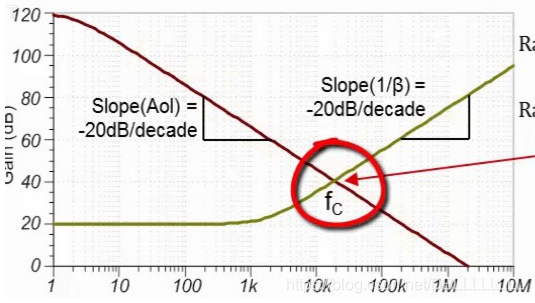
首先我们根据运算放大器的开环增益和反馈系数,绘制出开环增益曲线A和反馈系数的倒数 1 F \frac{1}{F} F1的幅频特性曲线。
然后找到两条曲线的交点,该交点的频率称为交叉频率 f x f_x fx。
找到子交叉频率下两条曲线的斜率: S l o p e ( A ) ∣ f = f x Slope(A)|_{f=f_x} Slope(A)∣f=fx和 S l o p e ( 1 / F ) ∣ f = f x Slope(1/F)|_{f=f_x} Slope(1/F)∣f=fx,
两个斜率的差的幅度称为截止速率ROC:
R
O
C
=
∣
S
l
o
p
e
(
A
)
−
S
l
o
p
e
(
1
/
F
)
∣
f
=
f
x
ROC=|Slope(A)-Slope(1/F)|_{f=f_x}
ROC=∣Slope(A)−Slope(1/F)∣f=fx
然后我们带入以下式子来估计该运算放大器的相位裕度
ϕ
m
\phi_m
ϕm:
R
O
C
=
20
d
B
/
d
e
c
→
ϕ
m
=
90
°
ROC=20dB/dec→\phi_m=90°
ROC=20dB/dec→ϕm=90°
R O C = 30 d B / d e c → ϕ m = 45 ° ROC=30dB/dec→\phi_m=45° ROC=30dB/dec→ϕm=45°
R O C = 40 d B / d e c → ϕ m = 0 ° ROC=40dB/dec→\phi_m=0° ROC=40dB/dec→ϕm=0°
R O C > 40 d B / d e c → ϕ m < 0 ° ROC>40dB/dec→\phi_m<0° ROC>40dB/dec→ϕm<0°
由此可见,如果两个曲线的斜率差大于等于40dB/dec,那么我们就认为该系统存在不稳定的可能,需要我们进行补偿。
举例来说:
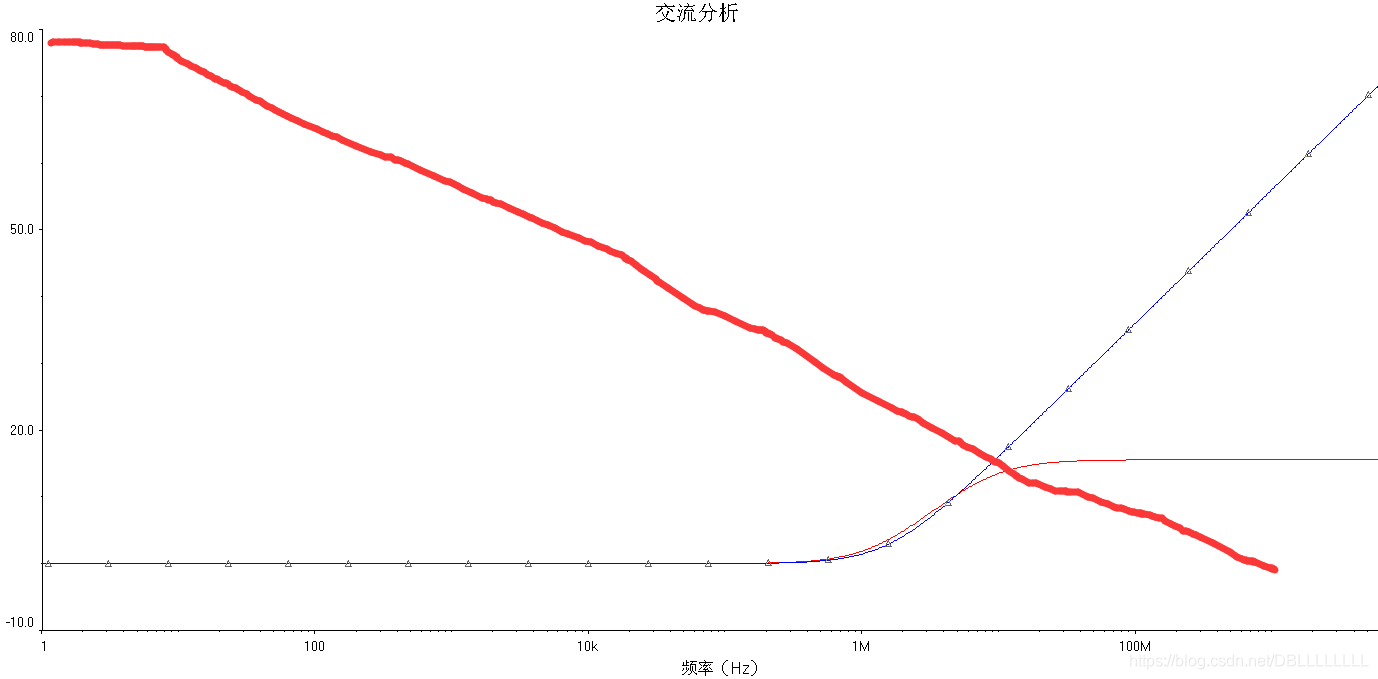
对于上图所示的电路,其反馈网络中存在阻抗元件,导致反馈系数为一个低通滤波器时,且低通滤波器的转角频率小于开环增益的单位增益频率,那么就会得到以下的两条曲线A和1/F:
可见,在交叉频率处,两曲线的斜率差为40dB/dec,那么此时系统就面临着稳定性的问题,处在振荡的边缘。(即使不振荡,由于相位裕度为0,因此此时的尖峰和振铃程度无限大,对于电路来说也是不可接受的)
4.3稳定性的补偿
如果我们的电路是不稳定的,那么如何来改善我们电路的性能,使得电路能够达到一定的稳定性呢?
我们的思路是,想办法在交叉频率处,使得截止速率减小。对于开环增益曲线,我们能做的不多,但是对于反馈系数F,我们却可以自行设计。因此我们的突破点就在于,如何修改电路,使得1/F曲线在交叉频率处的斜率小于20dB/dec。
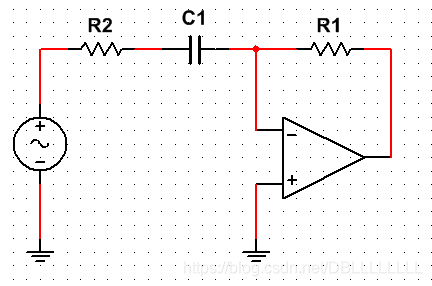
还是以刚才的电路图为例,第一种方法是,在电容旁边串联一个电阻R。
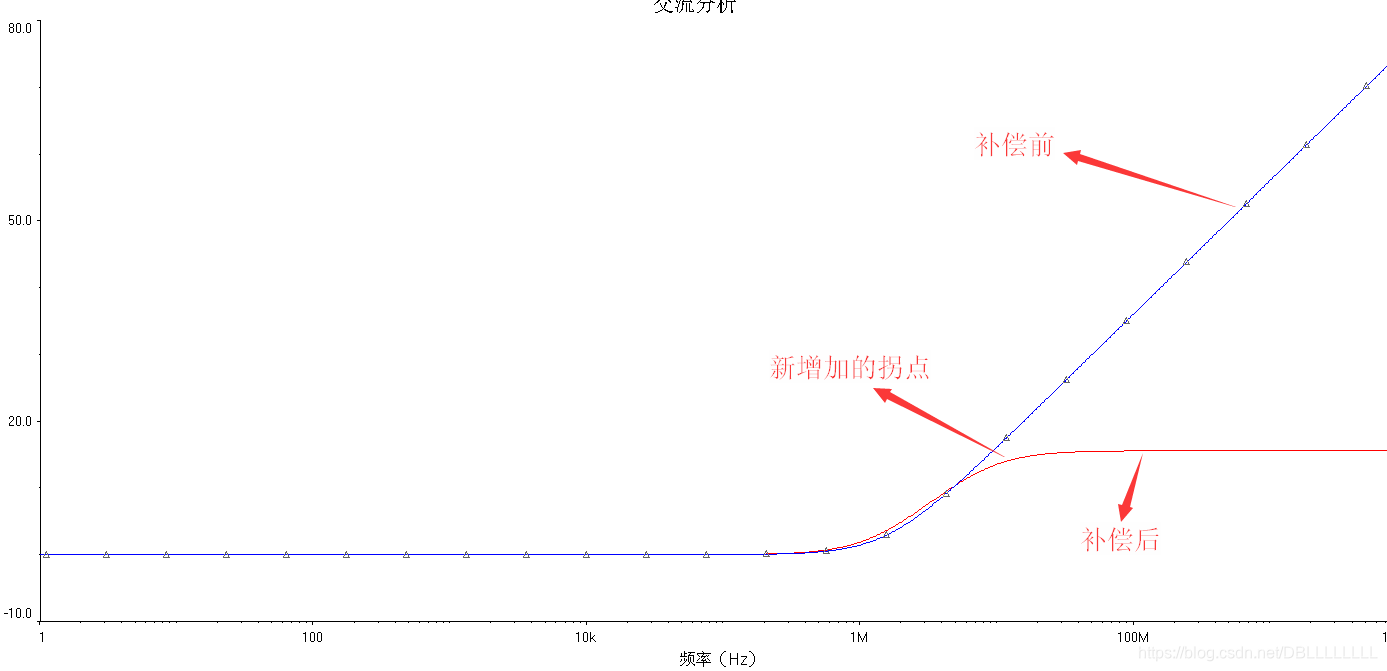
这样,1/F曲线就又增加了一个拐点,如下图:
如果新增加的拐点恰好为原来的交叉频率,则此时的ROC=30dB/dec,也就是说,系统具有45°的相位裕度。如下图:
如果需要更大的相位裕度,可以进一步缩小第二个拐点的频率,但是这是以进一步缩小接近理想为分期特性的频率范围为代价的。
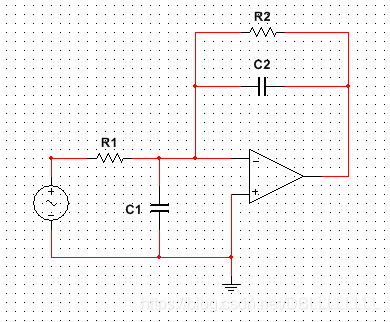
第二种方法是通过杂散电容的选择来进行补偿。
对于以下电路:
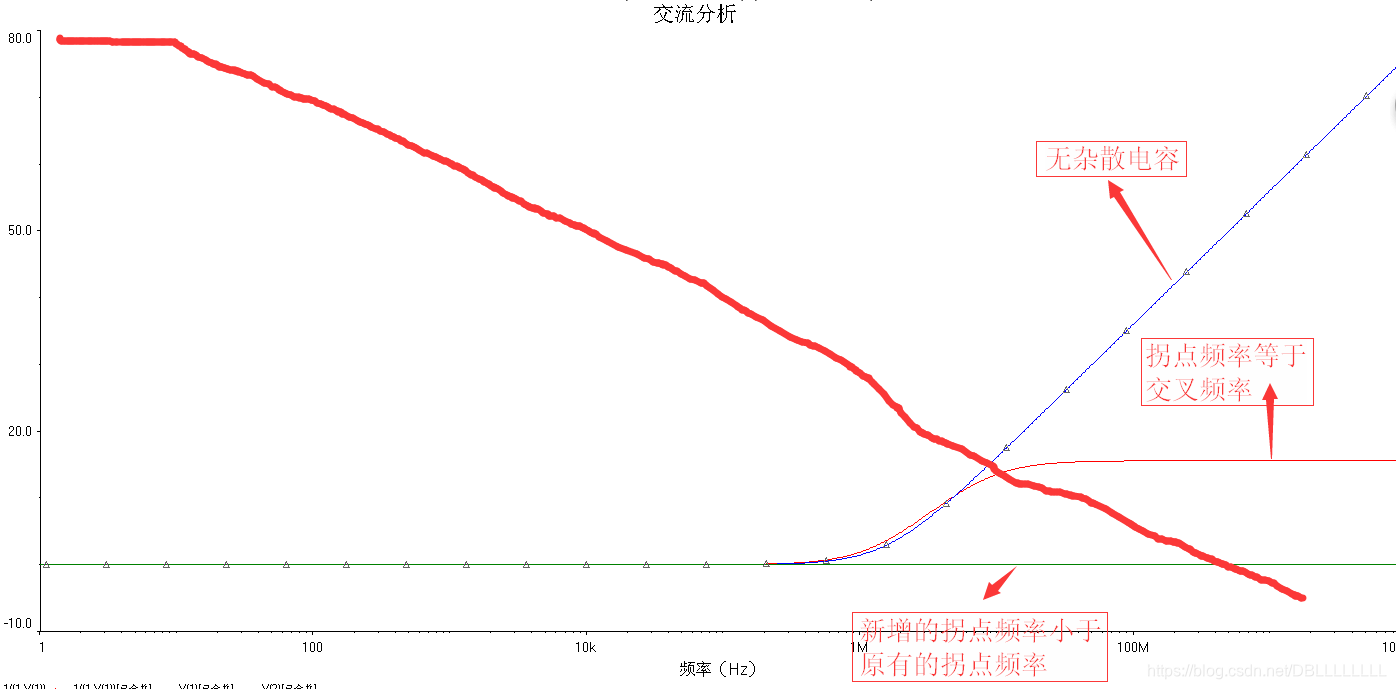
如果没有杂散电容C2的话,反馈系数曲线1/F只有一个拐点,因此在交叉频率处的ROC=40dB/dec,系统不稳定。
通过选择合理的C2,使得反馈系数曲线1/F新增加一个拐点,且新增加的拐点的频率等于原来的交叉频率,则此时的ROC=30dB/dec,系统的相位裕度为45°。
若新增加的拐点频率比原有的拐点频率还要小,那么反馈系数曲线1/F就是一条直线,此时ROC=20dB/dec,系统的相位裕度为90°。这种技术叫做中和补偿。
上述各种补偿行为,一般来说都是以牺牲带宽为代价。因此我们并不是一定要追求十分大的相位裕度,作为一名工程师,需要在各个参数之间寻找到平衡参数。