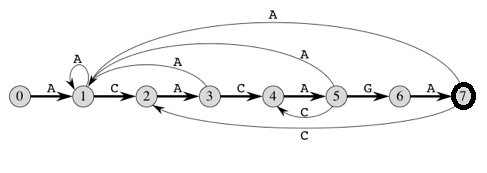
字符串模式匹配的的核心其实就是利用有限自动机（正则表达式引擎的核心就是这个）。所以问题的关键就是在于构建出结构正确的有限自动机，剩下的工作无非就是沿着自动机跑状态，直到终止状态，所以思想比较简单（一个有限自动机的示例如图，图中的状态数其实也就是已经匹配到的字符串的长度）：

但是，如何构造出来呢？核心思想就是利用已经匹配过的信息，以及一个归纳法：

首先，我们可以把自动机的主骨架写出来，很容易，就是根据模式串把一个个状态连接起来，这代表了完全匹配的情况；

接下来，对于不匹配的情况，我们假设我们已经知道了到第k-1状态时候所有不匹配情况的状态转移（当然也包括匹配情况的状态转移，也就是主骨架），那么我们怎么知道第k状态时的状态转移呢？在解决这个问题之前，我们需要以最直观，最naive的方式来分析一下这个问题：

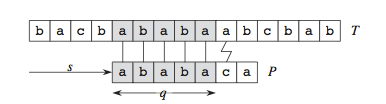
比如说上图，假设我们已经知道从状态0到状态(长度)5的转移信息，现在由于状态(长度)6不匹配了，我们要求状态6的转移信息。通常发现不匹配了，naive的做法是把模式串P向后移动一格，然后再从头开始匹配，当我们把模式向后移动一格以后，就会有下图：

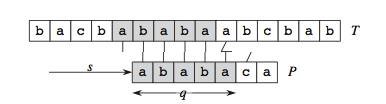
但是注意，这里由于我们已经假设了知道状态0到5的全部转移信息，我们实际上可以直接拿已经匹配过的串去匹配模式，换句话说就是拿模式的子串去匹配模式自身！最后匹配出来的状态数（长度）也就是模式串自身前后缀重合的最大长度，这个就是KMP的核心思想！！比如说上面那个例子，由于模式移动一格以后，需要与模式匹配的串（baba）的长度其实是4而非5，这点可以保证仅仅用6之前的状态转移信息就足够确定整个子串具体能匹配到哪一个状态了。所以，我们只要拿着那个子串去尚未构建完成的有限自动机上去跑一下，就可以知道这个子串会匹配（停留）到哪一个状态。那么接下来的新读入的字符（这里是a）所导向的下一状态也可以通过子串匹配所最终停留的状态来确定（这个最终停留的状态一定是0到5之间的）。而这个新导向的状态也恰恰就是状态6不匹配时且读入是a时候所应该转向的下一状态。

这样，通过前k-1个状态之间的转移信息，我们可以推出第k个状态的转移信息（具体做法就是把那k-1长度已匹配模式串去头以后放到自动机里去匹配模式串自身，然后确定第k状态该被导向哪）。比如我们有模式串ABABC，因为状态0已知，那么我们构造状态1时候的，实际上就是拿长度为0的空串去匹配ABABC, 这个匹配最后会停留在状态0，那么状态1不匹配时的转移就是状态0下对应的转移；接下来当我们构造状态2的时候，就是拿长度为1的去头子串B去匹配ABABC，最终2所对应的转移就是当前停留状态下的转移。进一步可以发现，这种归纳构造使得所有不匹配的转移都是导向之前的状态的(也就是所谓的back up, 或者退化degeneration)。而且我们知道对于状态0而言，所有的非匹配状态都是导向自身的。这样，通过归纳构造和利用已经构造出的有限自动机的匹配信息，我们最终可以够造出完整的有限自动机，从而实现模式匹配。

我们并不需要每次都把模式串的子串放到自动机中去跑一遍以确定对应的停留状态！比如我们有模式串ABABC，假设状态1已知，那么我们构造状态2时候的，实际上就是拿长度为1的串B去匹配ABABC, 这个匹配最后会停留在状态X，那么状态2不匹配时的转移就是状态X下对应的转移；接下来当我们构造状态3的时候，就是拿长度为2的去头子串BA去匹配ABABC，但是我们并不需要从头把BA放进去跑一遍，因为之前我们已经跑过一遍B了，而且我们知道最终停留在状态X，所以实际上我们只需要从X接着往下跑A就可以抵达下一个停留状态。这样，通过纪录当前已经抵达的停留状态X，我们可以通过一种递推的方式构造出这个有限自动机：

定义有限自动机为: DFA[input_char][current_state]; DFA[any_input][pattern.length] = STOP

那么首先初始化正确匹配的情况: DFA[pattern(j)][j] = j+1

接下来就是不匹配时候的递推式, 初始化状态: prev = 0, DFA[c][0] = 0, c!=pattern(0)

对所有状态j>0和不匹配的字符c (c!=pattern(j)):

LOOP:

prev = DFA[pattern(j)][prev]

DFA[c][j] = DFA[c][prev]

j++

按照以上方法构造的状态机虽然简单易懂，但是会占据O(n^2)的空间，一种更有效率的构造方式是仅仅追踪每个状态对应的prev状态，然后建立一种动态的有限自动机——每当读入一个新的字符以后，如果匹配，就状态数加一，否则回溯到prev状态，再看是否匹配。根据KMP状态机的结构特性，这样的过程最终会在0状态收敛。所以，很容易的，我们可以递推出所有状态发生不匹配时会退化到的prev状态，由于0状态本身不再退化，所以算法时收敛的。对于非零状态，我们知道状态数会递增当且仅当发生匹配且匹配连续时，一旦有不连续情况发生，则必然产生状态退化。

首先，注意到状态机对应的状态数和模式串pattern的关系是：状态k表示已经匹配了从pattern(0)到pattern(k-1)的字符，但是不确定能否匹配pattern(k)这个字符。

接下来我们可以模拟模式子串（去头子串pattern[1...n]）输入自动机的情况：

k=0

k++,如果pattern(k)!=pattern(0), 那么prev(k+1)=0; 当进行到第k位出现不匹配时，这时还未匹配任何字符，但是第一个字符就匹配不了，所以状态应该直接退化到0，对应状态机上0状态时那个指向自己的弧。

k++,如果pattern(k)==pattern(0), 那么prev(k+1)=1; 当进行到第k位时，已匹配模式首字符，所以如果第k+1个字符匹配失败后，直接退化到状态1. 下一次比较可以直接从pattern(1)开始。

k++,如果pattern(k)==pattern(1), 那么prev(k+1)=2; 当进行到第k位时，已连续匹配模式首两个字符，所以如果第k+1个字符匹配失败后，直接退化到状态2. 下一次比较可以直接从pattern(2)开始。

k++,如果pattern(k)==pattern(2), 那么prev(k+1)=3;当进行到第k位时，已连续匹配模式首三个字符，所以如果第k+1个字符匹配失败后，直接退化到状态3. 下一次比较可以直接从pattern(3)开始。

k++,如果pattern(k)!=pattern(3), 那么继续判断pattern(k)?=pattern(prev(3));当进行到第k位出现不匹配时，这时已经匹配了三个字符，但是第四个字符不匹配，所以状态应该直接退化到prev(3),然后从pattern(prev(3))开始重新匹配。如果继续不匹配，那么继续往前退化比较

pattern(k)?=pattern(prev(prev(3)))，直到出现结果pattern(k)==pattern(prev(...prev(prev(3))...))=>prev(k+1)=prev(...prev(prev(3))...)+1或者收敛到0.

假设t是“连击数”，那么一般的：

k++,如果pattern(k)==pattern(t),那么prev(k+1)=t+1, t++; 当进行到第k位时，已连续匹配模式首t+1个字符，所以如果第k+1个字符匹配失败后，直接退化到状态t+1，下一次比较可以直接从pattern(t+1)开始。; 如果pattern(k)!=pattern(t), 当进行到第k位出现不匹配时，这时已经匹配了t个字符，但是第t+1个字符不匹配，所以状态应该直接退化到prev(t),然后从pattern(prev(t))开始重新匹配。如果继续不匹配，那么继续往前退化比较 

pattern(k)?=pattern(prev(prev(t)))，直到出现结果pattern(k)==pattern(prev(...prev(prev(t))...))=>prev(k+1)=prev(...prev(prev(t))...)+1或者收敛到0.

以上过程其实就是教材KMP算法的核心，KMP Table 的构造。prev值实际上就是出现不匹配时模式串自我匹配时前后缀最大重叠长度，这个值可以被用来直接跳过模式串自我重合的区域，从而达到搜索速率的最优化。

以下是对应LeetCode strStr() 题目的代码，由于要处理一些特殊情况，所以逻辑会复杂一点，但是基本思想不变：

if(needle=="") return haystack;
        //KMP table formation
        int[] prev = new int[needle.length()];
        prev[0]=0;
        int t=0;
        if(needle.length()>1){
        	prev[1]=0;
        	for(int i=2;i<needle.length();i++){
        		while(t>0&&needle.charAt(i-1)!=needle.charAt(t)) t = prev[t];
        		if(needle.charAt(i-1)==needle.charAt(t)){
        			prev[i]=t+1;
        			t++;
        		}else if(t==0) prev[i]=t;
        	}
        }
        //KMP search
        t=0;
        for(int i=0;i<haystack.length();i++){
            while(t>0&&haystack.charAt(i)!=needle.charAt(t)) t = prev[t];
            if(haystack.charAt(i)==needle.charAt(t)) t++;
            if(t==needle.length()){
                return haystack.substring(i-t+1);
            }
        }
        return null;