前言
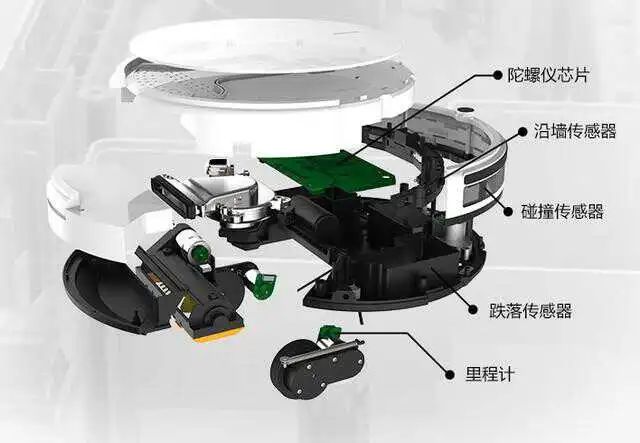
扫地机器人是现代家庭中最常见的智能设备。其基本的核心组件由主控系统(大脑)、传感器等控制系统(感知系统)、动力供应系统(心脏)、清扫系统(四肢)组成。
扫地机器人的智能、高效、灵活程度,最重要的核心技术便是路径的设计与规划,比如自主地实现避障,在不同地形如木地板、砖地板、地毯、地垫等以及各种障碍物的情况下进行实时决策、移动、清扫等任务。
扫地机器人的路径规划是机器人学科中的一个重要研究领域,其中如何在清扫过程中规划出最优路径,确保覆盖整个区域并避开障碍物,这就需要借助算法了。
最常见的最短路径算法包括 Dijkstra(迪杰斯特拉)算法、A* 算法、Bellman-ford(贝曼-福特)算法、Floyd-Warshall (佛洛依德-沃歇尔)算法等,这些都属于不同的最短路径算法。
用嬴图数据库来建模扫地机器人的路径规划:
1、创建图模型[5] :
· 点[1] 可以代表扫地机器人可以访问的房间、走廊、墙角、家具等每个地点;
· 边 [2] 则用来表示点与点之间的连接,例如路径的长度,通行的难度(例如需要穿过狭窄的门或地毯)、路径类型(直线、曲线、斜坡等)等。
2、节点属性:
· 每个节点可以具有属性,如节点的坐标、类型(起点、终点、障碍物等),是否被清扫过等状态信息。这些属性均可以帮助扫地机器人进行路径[3] 规划和决策。
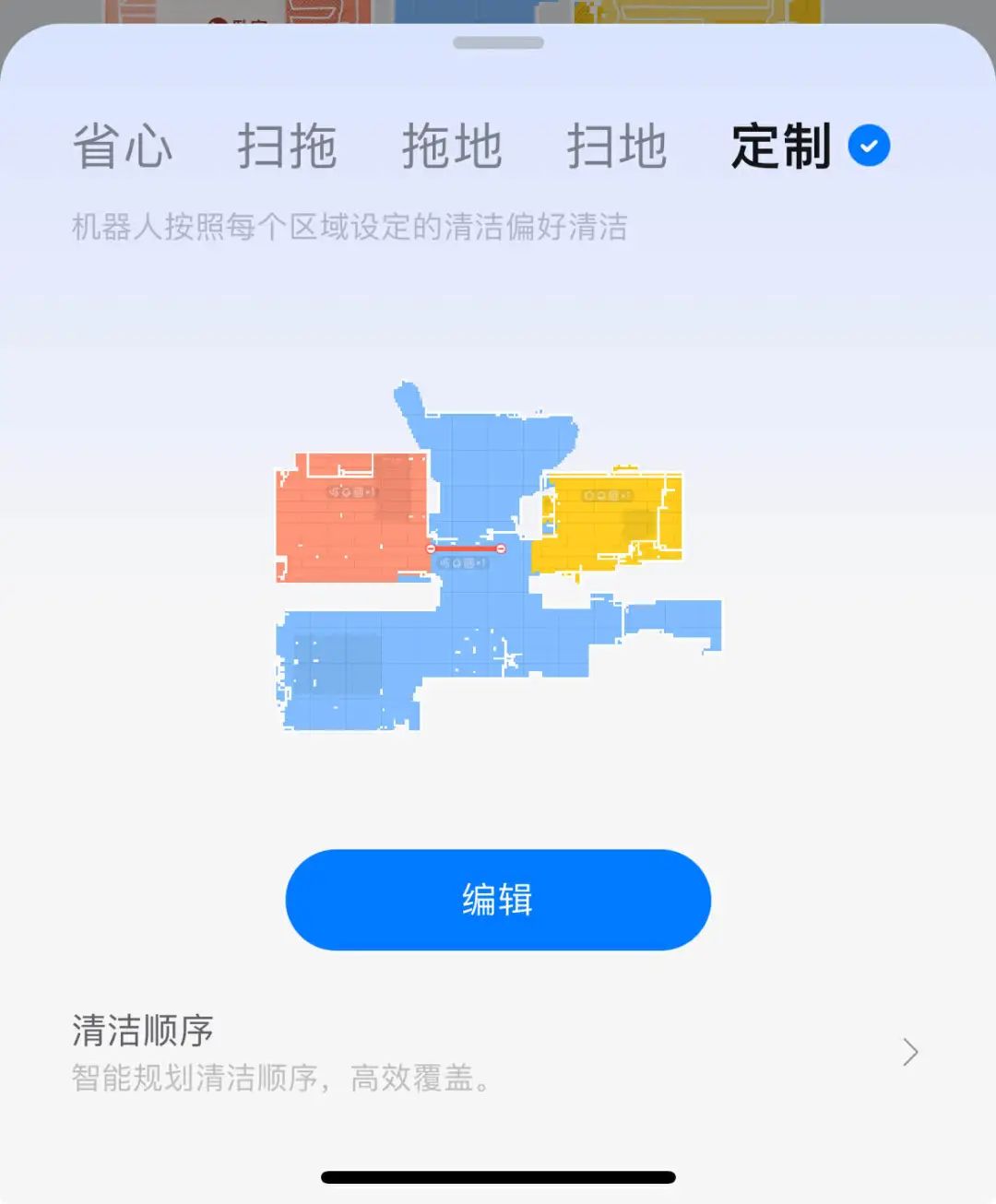
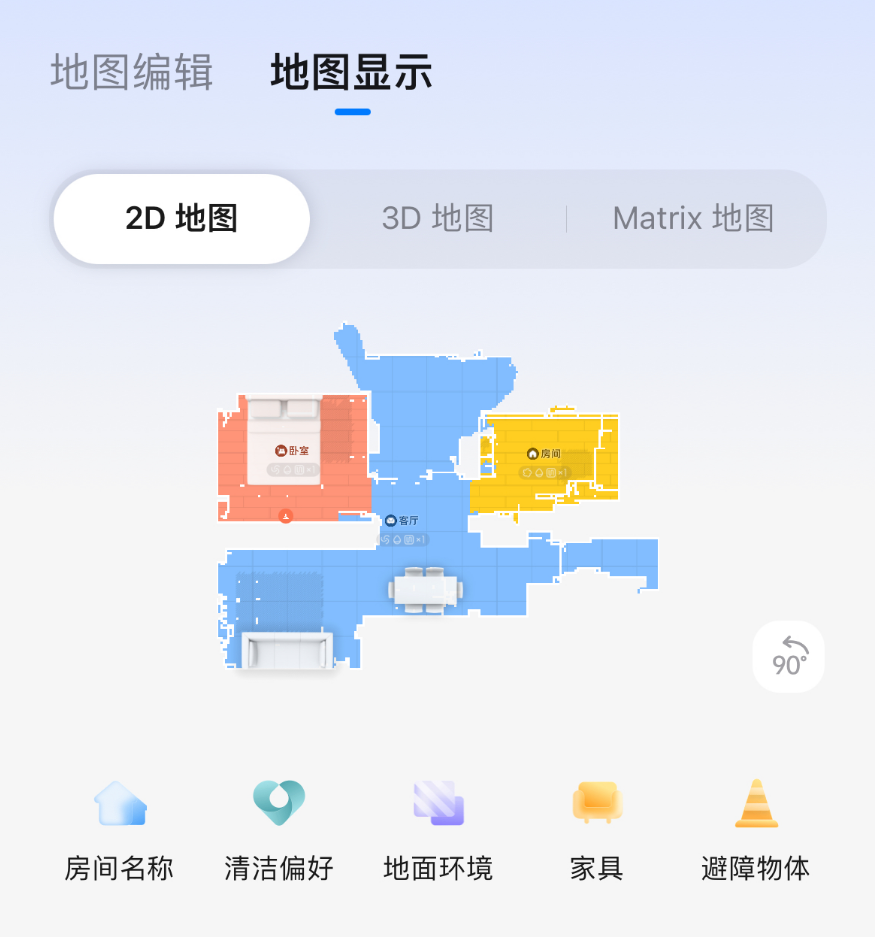
在我们日常中,呈现出的上层应用显示见下图:
3、最短路径[4] 算法:
基于以上的建模信息,扫地机器人可以通过 Dijkstra 算法、A* 算法等来快速找到从起点到终点的最优路径。
1) Dijkstra(迪卡斯特拉)算法:在离散化的清扫区域网格中,机器人可以根据这个算法计算出一条能够有效覆盖整个区域的路径。
该算法的主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
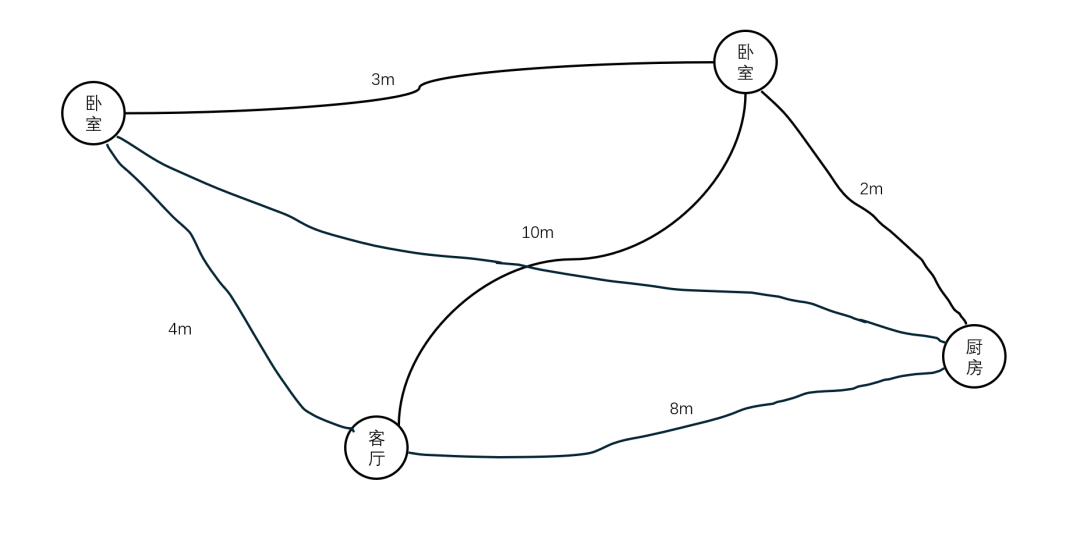
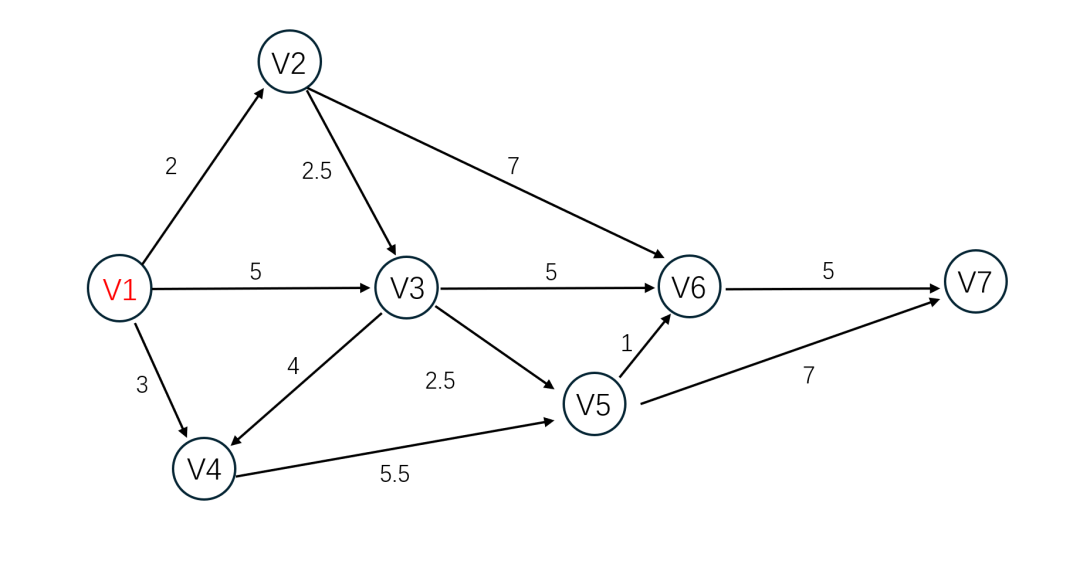
图中各边上的每个数字表示从起始节点到终止结点的距离(这里定义为权值/权重)。那么,如上图所示,V1到各点之间的最短路径是哪些?使用方法如下:
| 起点 | 终点 | 最短路径 | 距离 |
| V1 | V2 | V1—V2 | 2 |
| V1 | V3 | V1—>V2—>V3 | 4.5 |
| V1 | V4 | V1—>V4 | 3 |
| V1 | V5 | V1—>V2—>V3—>V5 | 7 |
| V1 | V6 | V1—>V2—>V3—>V5—>V6 | 8 |
| V1 | V7 | V1—>V2—>V3—>V5—>V6—>V7 | 13 |
2)A*(A-Star)算法:扫地机器人通过 A*算法结合启发式函数,可以在清扫过程中动态地规划最短路径,并充分去考虑房间的布局和障碍物的分布,从而提高路径规划效率。
A*算法的优点是速度快,它通过评估每个节点到终点的距离,选择最优的路径来搜索最短路径。A*算法使用一个路径优劣评价公式为:
f ( n ) = g ( n ) + h ( n )
这里面还涉及到一个扫地机器人如何执行避障算法的问题。扫地机器人可以使用基于图搜索的算法如 A*来规划避开障碍物的路径,确保在清扫过程中不会与障碍物碰撞。
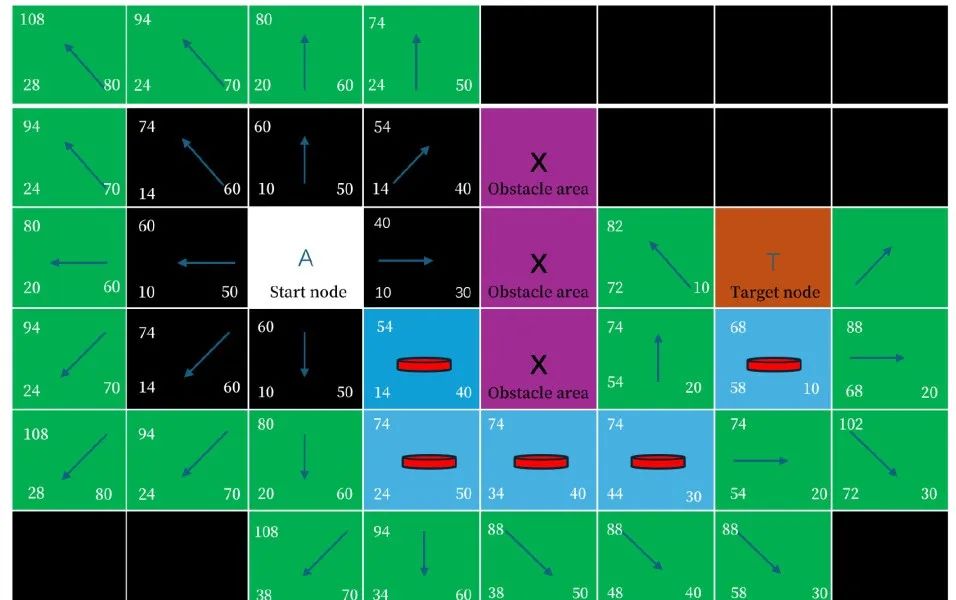
如图,假设我们需要从 A 点到目标点,这两点之间有一堵墙。我们把地图栅格化,把每一个方格的中心称为节点;父节点 A 周围共有 8 个子节点。这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子,它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 目标点需要走过哪些方格,就找到了路径。一旦路径找到了,便从一个方格的中心移动到另一个方格的中心,直至到达目的地 T。
3)最小生成树(Minimum Spanning Tree,MST)算法:这些算法可以用于优化机器人的清扫路径,确保覆盖整个区域的同时减少路径长度,提高清扫效率。
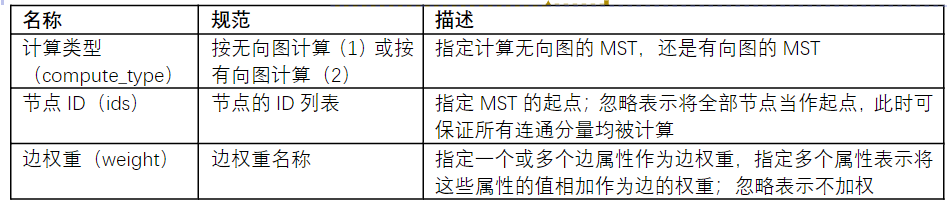
最小生成树算法是一种试图选出权重[6] 和最小的边,从而使全图节点尽可能连通的算法。它属于图论中的一个基本概念,主要应用于路径优化、寻求最低成本等降本增效的求解场景中。以下是最小生成树算法的常用参数。
在实际应用场景中,是会遇到动态变化以及要考虑各种复杂性的,图数据库可以支持动态的更新点和边,这就使得扫地机器人在路径规划时,可以根据实时环境的变化随时进行调整。(值得注意的是,图要考虑可能有环的问题,这意味着我们可从一个节点出发,走一圈后又回到这个节点。我们只要每绕环一次,总权重都会增加。因此,绕环的路径不可能是最短的路径。)
最后,扫地机器人的机智程度还需依托无线传感技术来及时观测发现,其中,该技术在无线传感网络中的应用也会用到最小生成树算法。该算法将实时观测到的环境信息、设备、路由等所有的网络进行建模,一旦当某个因素出现变化时,那么物理距离上代表图中的边上的权重也会实时更新,随之边权重相关的最小生成树计算必然也会实时调整,最终确保扫地机器人在清扫过程中轻松应对障碍物阻塞或各种突发情况。
小结:
综上所述,随着物联网的普及,算法的应用正在为日常生活带来更多智能化的体验,尤其随着人工智能和机器学习技术的不断进步,未来将有更多的技术为家庭生活带来更多的便利和舒适。(文/Emma wanyi)
【注释】
【1】点 (Node):代表真实世界中的实体,即图论中的顶点(Vertex),在嬴图系统中也称作节点。
【2】边 (Edge):代表真实世界中实体间的关系,连接两个实体。嬴图系统中的边均为有向边。边的两个端点可以相同也可以不同,相同时称为自环边(Self-loop)。
【3】路径 (Path):有确定的起点和终点、由点边交替相连构成的序列称为路径。路径中点可以重复出现,边不能重复出现。路径中所有点、边组成的序列可看作为路径的唯一标识符。
【4】最短路径 (Shortest Path):从起点经过最少的边(至少一条)到达终点的路径称为该起点到该终点的最短路径。当边带有权重时,“最少的边”应理解为“权重和最小的边”。
【5】图模型 (Graph Model):图中所有 schema 和属性的定义,表达图所描述的具体场景。
【6】权重(weight):狄克斯特拉算法用于每条边都有关联数字的图,这些数字称为权重(weight)。带权重的图称为加权图(weighted graph),不带权重的图称为非加权图(unweighted graph)。
END
对图算法更多了解,请阅读嬴图系列2024年度新书——《图算法:行业应用与实践》,本书是继《图数据库原理、架构与应用》的姊妹篇。