引言
如今最为重要的数据模型便是关系模型。关系数据库就是支持关系模型的数据库系统(Relational Database Management System, RDBMS)
-
关系模型可以简单理解为二维表格模型,一个关系型数据库就是由二维表及其之间的关系组成的一个数据组织。
-
关系型数据库是指采用了关系模型来组织数据的数据库。它以行和列的形式存储数据,这些行和列组成的结构被称为表,一组表则组成了数据库。
-
关系型数据库通过表之间的主键(Primary Key)和外键(Foreign Key)关系来建立数据之间的联系,从而构成了一个复杂的数据组织系统。
-
用户通过查询来检索数据库中的数据,而查询是一个用于限定数据库中某些区域的执行代码。
关系型数据
关系模型的数据结构
关系模型的数据结构非常简单,只包含单一的数据结构——关系。在用户看来,关系模型中数据的逻辑结构是一张扁平的二维表。
关系模型的数据结构虽然简单却能够表达丰富的语义,描述出现实世界的实体以及实体间的各种联系。在关系模型中,现实世界的实体以及实体间的各种联系均用单一的结构类型,即关系来表示。
关系模型是建立在集合代数的基础上的,这里从集合论角度给出关系数据结构的形式化定义:
-
域(domain):域是一组具有相同数据类型的集合。例如,自然数、整数、实数、长度小于25 字节的字符串集合、{0,1}、{男,女}、大于等于 0 且小于等于 100 的正整数等,都可以是域。
-
笛卡尔积(cartesian product):域上的一种集合运算。得到每个域中元素的所有可能的组合,它可以表示为一张二维表,在笛卡尔积中有:
- 元组:每一行是一个元组
- 分量:每一行中每一个元素都是一个分量xx
-
关系(relation): D 1 × D 2 × . . . × D n D_1 \times D_2 \times...\times D_n D1×D2×...×Dn 的子集叫做在域 D 1 , D 2 , . . . , D n D_1,D_2 ,...,D_n D1,D2,...,Dn 上的关系,表示为 R ( D 1 , D 2 , . . . , D n ) R(D_1,D_2 ,...,D_n) R(D1,D2,...,Dn)
关系
R ( D 1 , D 2 , . . . , D n ) R(D_1,D_2 ,...,D_n) R(D1,D2,...,Dn)
R R R 表示关系的名字, n n n 是关系的目或度(degree)。关系中的每个元素是关系中的元组,通常用 t t t 表示。
- 当 n = 1 时,称该关系为单元关系(unaryrelation),或一元关系。
- 当 n = 2 时,称该关系为二元关系(binaryrelation)。
关系是笛卡儿积的有限子集,所以关系也是一张二维表,表的每行对应一个元组,表的每列对应一个域。
一般来说, D 1 × D 2 × . . . × D n D_1 \times D_2 \times...\times D_n D1×D2×...×Dn 的笛卡儿积是没有实际语义的,只有它的某个真子集才有实际含义。
码和属性
-
码:指的是一组属性的集合,通过这组属性可以唯一地标识关系模式中的每一个元组。在实际应用中,码(Key)至少是一个超码,且满足关系模式中的每一个元组都有唯一的键值组合,所有的键值组合都是不可分的。
-
属性:由于域可以相同,为了加以区分,必须对每列起一个名字,称为属性(attribute)。n 目关系必有 n 个属性。
-
候选码:若关系中的某一属性组的值能唯一地标识一个元组,而其子集不能,则称该属性组为候选码(candidate key)。候选码不一定只有一个,也可能有多个,只要满足条件即可
-
主码:某个能够唯一标识一条记录的最小属性集,若一个关系有多个候选码,则选定其中一个为主码(primary key)。
-
主属性:候选码的诸属性称为主属性(primeattribute)。
-
非主属性:不包含在任何候选码中的属性称为非主属性(non-primeattribute)或非码属性(non-keyattribute)。
-
超码:能够唯一标识一条记录的属性或属性集,其中可包含不相关的非主属性,称为超码(super key),超码是候选码的扩充,候选码是最小的超码
-
全码:在最极端的情况下,关系模式的所有属性是这个关系模式的候选码,称为全码(all-key)。
关系的类型
关系可以有三种类型:
-
基本关系(又称为基本表):实际存在的表,是实际存储数据的逻辑表示
-
查询表:查询结果对应的表
-
视图表:由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
基本关系
基本关系具有以下 6 条性质:
-
列是同质的(homogeneous),即每一列中的分量是同一类型的数据,来自同一个域
-
不同的列可出自同一个域,称其中的每一列为一个属性,不同的属性要给予不同的属性名。
-
列的顺序无所谓,即列的次序可以任意交换。由于列顺序是无关紧要的,因此在许多实际关系数据库产品中增加新属性时,永远是插至最后一列。
-
任意两个元组的候选码不能取相同的值。
-
行的顺序无所谓,即行的次序可以任意交换。
-
分量必须取原子值,即每一个分量都必须是不可分的数据项。
关系模型要求关系必须是规范化(normalization)的,即要求关系必须满足一定的规范条件。这些规范条件中最基本的一条就是,关系的每一个分量必须是一个不可分的数据项(第一范式 1NF)。
关系模式
在数据库中要区分型和值。关系数据库中,关系模式是型,关系是值。
关系模式是对关系的描述。关系是元组的集合,因此关系模式必须描述:
-
这个元组集合的结构,即它由哪些属性构成,这些属性来自哪些域,以及属性与域之间的映像关系。
-
元组语义以及完整性约束
-
属性之间的数据依赖关系
关系模式可表示为: R ( U , D , D O M , F ) R(U,D,DOM,F) R(U,D,DOM,F)
- R R R:关系名
- U U U:组成该关系的属性名集合
- D D D: U U U 中属性所来自的域
- D O M DOM DOM:属性向域的映像集合
- F F F:属性间数据的依赖关系集合
关系模式通常可简记为: R ( U ) R(U) R(U) 或 R ( A 1 , A 2 , . . . , A n ) R(A_1,A_2,...,A_n) R(A1,A2,...,An)
- R R R:关系名
- A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An:属性名
- 域名及属性向域的映像常常直接说明为属性的类型、长度。
将关系模式看作一个三元组
R < U , F > R<U,F> R<U,F>
当 U U U 上的一个关系 r r r 满足 F F F 时, r r r 称为关系模式 R < U , F > R<U,F> R<U,F> 的一个关系
- R R R:关系名
- U U U:组成该关系的属性名集合
- F F F:属性间数据的依赖关系集合
关系是关系模式在某一时刻的状态或内容。关系模式是静态的、稳定的,而关系是动态的、随时间不断变化的,因为关系操作在不断地更新着数据库中的数据。例如,学生关系模式在不同的学年,学生关系是不同的。
关系模型的存储结构
在关系数据模型中,实体及实体间的联系都用表来表示,但表是关系数据的逻辑模型。
在关系数据库的物理组织中,有的关系数据库管理系统中一个表对应一个操作系统文件,将物理数据组织交给操作系统完成;有的关系数据库管理系统从操作系统那里申请若干个大的文件,自己划分文件空间,组织表、索引等存储结构,并进行存储管理。
关系操作
关系模型中常用的关系操作包括查询操作(query)和更新操作(插入(insert)、删除(delete)、修改(update))两大部分。
关系的查询表达能力很强,是关系操作中最主要的部分。查询操作又可以分为选择、投影、连接、除、并、差、交、笛卡儿积等。其中选择、投影、并、差、笛卡儿积是 5 种基本操作,其他操作可以用基本操作来定义和导出,就像乘法可以用加法来定义和导出一样。
关系操作的特点是集合操作方式,即操作的对象和结果都是集合。这种操作方式也称为一次一集合(set-at-a-time)的方式。相应地,非关系数据模型的数据操作方式则为一次一记录(record-at-a-time)的方式。
关系运算
关系代数是一种抽象的查询语言,用于对关系运算来表达查询
关系代数的运算对象和运算结果都是关系,所用到运算符可分为如下两种:传统的集合运算、专门的关系运算
数据库关系运算是指对数据库中的关系进行特定操作以得到新的关系的过程,是以集合操作为基础的运算,包括选择、投影、连接、除、并、差、交、笛卡儿积 共八种运算方式。
| 运算符 | 含义 | 英文 |
|---|---|---|
| ∪ ∪ ∪/ ∨ ∨ ∨ | 并 | Union |
| − − − | 差 | Difference |
| ∩ ∩ ∩/ ∧ ∧ ∧ | 交 | Intersection |
| × × × | 笛卡尔积 | Cartesian Product |
| σ σ σ | 选择 | Selection |
| π π π | 投影 | Projection |
| ⋈ ⋈ ⋈/ ∞ ∞ ∞ | 链接 | Join |
| ÷ ÷ ÷ | 除 | Division |
基本的关系代数运算
运算从行的角度进行
并(Union)
关系 R 与 S 具有相同的关系模式,即 R 与 S 的元数相同(结构相同),R 与 S 的并是属于 R 或 属于 S 的元组构成的集合,记作 R ∪ S,定义如下:
R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R∪S=\{t|t∈R∨t∈S\} R∪S={t∣t∈R∨t∈S}
在 SQL 中,可以使用 UNION 关键字进行计算。
差(Difference)
关系 R 与 S 具有相同的关系模式,关系 R 与 S 的差是属于 R 且 不属于 S 的元组构成的集合,记作 R − S,定义如下:
R − S = { t ∣ t ∈ R ∧ t ∉ S } R−S=\{t|t∈R∧t∉S\} R−S={t∣t∈R∧t∈/S}
在 SQL 中,可以使用 EXCEPT 或 MINUS 关键字进行计算。
广义笛卡尔积(Extended Cartesian Product)
两个无数分别为 n 目和 m 目的关系 R 和 S 的 笛卡尔积是一个 (n+m) 列的元组的集合。组的前 n 列是关系 R 的一个元组,后 m 列是关系 S 的一个元组,记作 R × S,定义如下:
R × S = { t ∣ t = < ( t n , t m ) ∧ t n ∈ R ∧ t m ∈ S } R×S=\{t|t=<(t^n,t^m)∧t^n∈R∧t^m∈S\} R×S={t∣t=<(tn,tm)∧tn∈R∧tm∈S}
( t n , t m ) (t^n,t^m) (tn,tm) 表示元素 t n t^n tn 和 t m t^m tm 拼接成的一个元组
在 SQL 中,可以使用 JOIN 关键字进行计算。
投影(Projection)
投影运算是从关系的垂直方向进行运算,从一个关系中选取出指定的属性组成一个新关系的操作,即在关系 R 中选出若干属性列 A 组成新的关系,记作 π A ( R ) π_A(R) πA(R),其形式如下:
π A ( R ) = { t [ A ] ∣ t ∈ R } π_A(R)=\{t[A]|t∈R\} πA(R)={t[A]∣t∈R}
在 SQL 中,可以使用 SELECT 关键字进行计算。
选择(Selection)
选择运算是从关系的水平方向进行运算,从一个关系中选择出符合某种条件的元组组成一个新关系的操作,即从关系 R 中选择满足给定条件的元组,记作 σ F ( R ) σ_F(R) σF(R),其形式如下:
σ F ( R ) = { t ∣ t ∈ R ∧ F ( t ) = T r u e } σ_F(R)=\{t|t∈R∧F(t)=True\} σF(R)={t∣t∈R∧F(t)=True}
在 SQL 中,可以使用 WHERE 关键字进行计算。
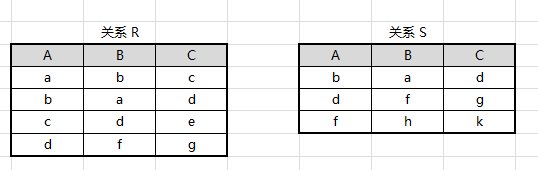
实例
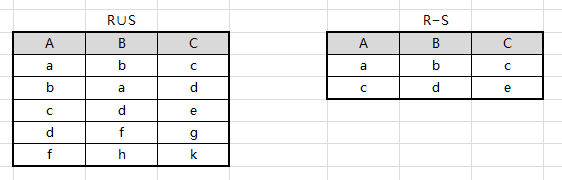
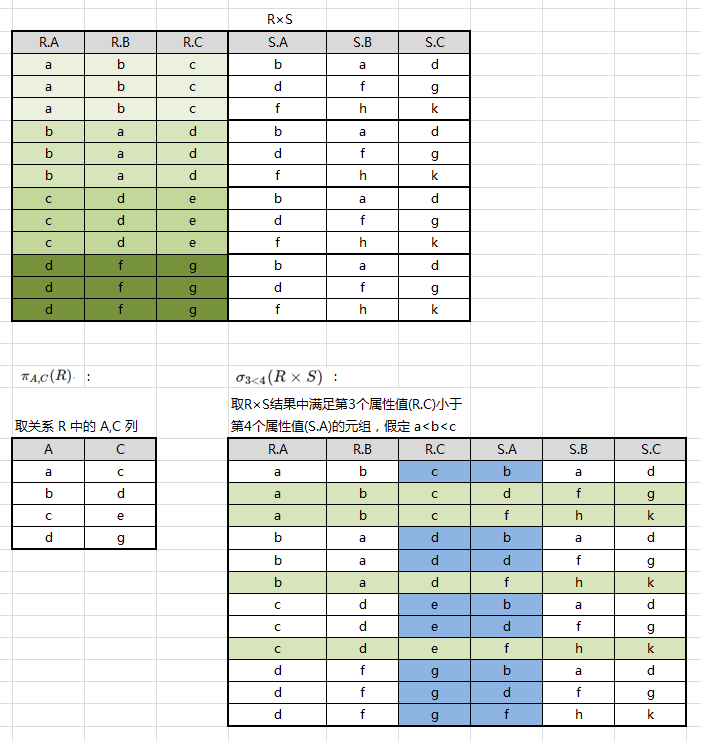
设有关系 R、S 如图所示,求 R ∪ S R∪S R∪S、 R − S R−S R−S、 R × S R×S R×S、 π A , C ( R ) π_{A,C}(R) πA,C(R)、 σ A > B ( R ) σ_{A>B}(R) σA>B(R) 和 σ 3 < 4 ( R × S ) σ_{3<4}(R×S) σ3<4(R×S)
进行并、差运算后结果如下:
进行笛卡尔、 投影、 选择运算后结果如下:
扩展的关系代数运算
交(Intersection)
关系 R 和 S 具有相同的关系模式,交是由属于 R 同时属于 S 的元组构成的集合,记作 R∩S,形式如下:
R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R∩S=\{t|t∈R∧t∈S\} R∩S={t∣t∈R∧t∈S}
链接(Join)
一般的连接操作是从 行 的角度进行的运算
注:下面的 θ 链接应该记作:
θ 链接
从 R 与 S 的笛卡尔积中选取属性间满足一定条件的元组,可由基本的关系运算笛卡尔积和选取运算导出,表示为:
R ⋈ { X θ Y } S = σ { X θ Y } ( R × S ) R \Join\{XθY\} S = σ\{XθY\}(R×S) R⋈{XθY}S=σ{XθY}(R×S)
X θ Y XθY XθY 为链接的条件,θ 是比较运算符,X 和 Y 分别为 R 和 S 上度数相等且可比的属性组
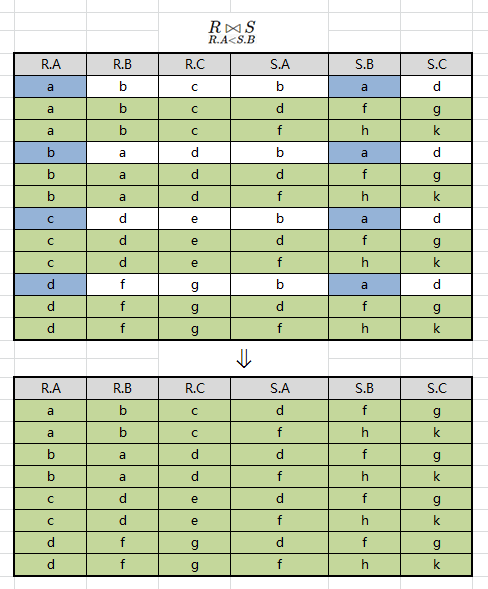
例如:求 R ⋈ R . A < S . B S R \Join_{R.A<S.B} S R⋈R.A<S.BS,如果为:
等值链接
当 θ 为「=」时,称之为等值链接,记为: R ⋈ X = Y S R\Join_{X=Y}S R⋈X=YS
等值连接必须要有等值的条件,当条件不同时连接的结果也不相同,两个关系可以没有相同的属性列
自然链接
自然连接是从 行和列 的角度进行的运算。
自然链接是一种特殊的等值链接,它要求两个关系中进行比较的分量必须是 相同的属性组,即必须要有相同的属性列,并且在结果集中将重复的属性列去掉
在 SQL 中,可以使用 JOIN 关键字并省略连接条件进行计算。
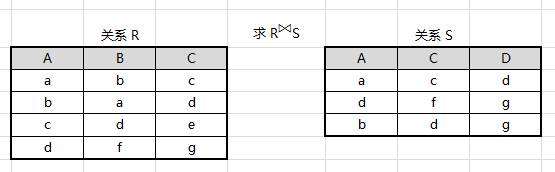
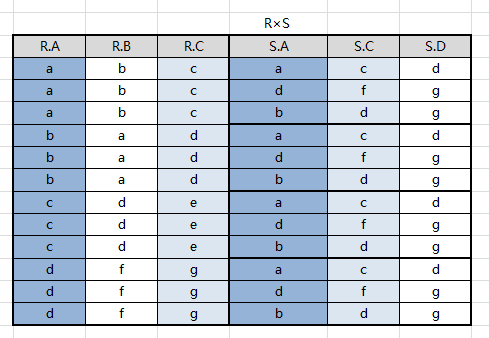
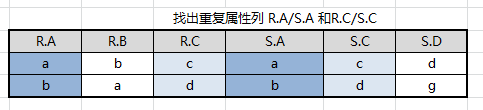
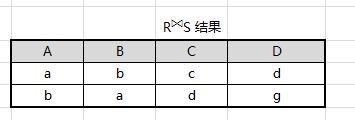
例如:设有关系 R、S 如图所示,求 R ⋈ S R \Join S R⋈S
先求出笛卡尔积
R
×
S
R×S
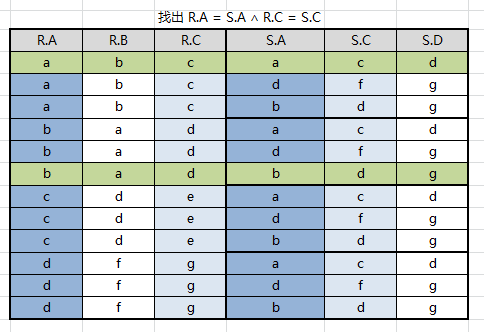
R×S,找出比较分量(有相同属性组),即: R.A/S.A 与 R.C/S.C
取等值链接 R . A = S . A R.A = S.A R.A=S.A 且 R . C = S . C R.C = S.C R.C=S.C
结果集中去掉重复属性列,注意无论去掉 R.A 或者 S.A 效果都一样,因为他们的值相等,结果集中只会有属性 A、B、C、D
最终得出结果
除(Division)
除运算是指从一个关系中筛选出满足条件的元组并按照给定关系的属性集合进行组合的操作,该元组与给定的关系在所有其他属性上的组合保持一致。
在 SQL 中,可以使用 DIVIDE 关键字进行计算。
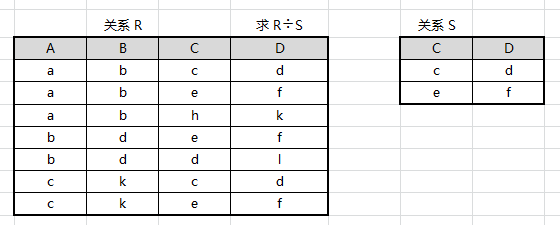
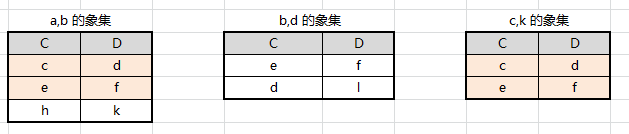
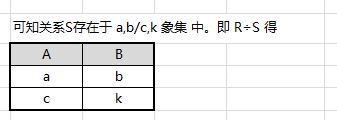
设有以下如图关系,求 R ÷ S R÷S R÷S
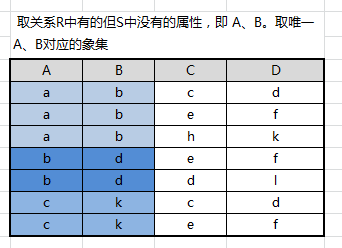
取关系 R 中有的但 S 中没有的属性组,即:A、B
取唯一 A、B 属性组值的象集
可知关系 S 存在于 a,b/c,k 象集 中。即 R ÷ S R÷S R÷S 得
关系型语言分类
关系语言是用于管理和查询关系型数据库的语言,它们依据不同的理论基础和表达方式可以被分类为以下几类:
-
关系代数语言:
- 这类语言基于数学上的关系代数理论,使用集合操作如并集(UNION)、交集(INTERSECT)、差集(MINUS)、笛卡尔积(CROSS PRODUCT)以及选择(SELECT)、投影(PROJECT)、连接(JOIN)等操作来表达查询需求。
- 例子:ISBL(Interface Set Based Language)是一种早期的关系代数语言。
-
关系演算语言:
- 关系演算语言基于一阶逻辑,允许用户通过谓词逻辑表达查询需求,而不必关心如何从物理存储中获取数据。
- 可以细分为:
- 元组关系演算语言:谓词变元的基本对象是元组变量,如
APLHA和QUEL。 - 域关系演算语言:谓词变元的基本对象是域变量,
QBE(Query By Example)是这种语言的典型代表。
- 元组关系演算语言:谓词变元的基本对象是元组变量,如
-
SQL(Structured Query Language):
SQL结合了关系代数和关系演算的特性,是一种高度非过程化的语言,允许用户定义和操纵数据,同时也支持事务处理、数据控制和数据字典维护等功能。- SQL已经成为关系数据库的标准语言,几乎所有现代的关系型数据库管理系统都支持SQL。
这些语言的主要特点包括:
- 完备的表达能力:能够表达所有关系代数和关系演算能够表达的查询。
- 非过程化:用户只需描述所需的数据,而不需要指定数据如何被获取。
- 集合操作:操作的对象是数据的集合,而不是单个记录。
- 功能性:能够嵌入到高级程序设计语言中使用,提供强大的数据处理能力。
关系语言的设计目标是提供一种自然、直观的方式来表达数据查询和操作,同时保证数据的完整性和一致性。SQL作为关系语言的代表,已经成为了行业标准,被广泛应用于商业、教育、科研等各种领域。
关系型数据库
关系型数据库就是支持关系模型的数据库系统,即在一个给定的应用领域中,所有关系的集合构成的一个关系数据库
关系数据库也有型和值之分:
-
关系数据库的型:也称为关系数据库模式,是对关系数据库的描述。包括若干域的定义,以及在这些域上定义的若干关系模式
-
关系数据库的值:这些关系模式在某一时刻对应的关系的集合,通常就称为关系数据库。
关系完整性约束
关系模型的完整性规则是对关系的某种约束条件,即关系的值随着时间变化时应该满足一些约束条件。这些约束条件实际上是现实世界的要求。任何关系在任何时刻都要满足这些语义约束。
关系模型中有三类完整性约束:
- 实体完整性(EntityIntegrity)
- 参照完整性(ReferentialIntegrity)
- 用户定义的完整性(User-defined Integrity)。
其中实体完整性和参照完整性是关系模型必须满足的完整性约束条件,被称作是关系的两个不变性,应该由关系系统自动支持。用户定义的完整性是应用领域需要遵循的约束条件,体现了具体领域中的语义约束。
实体完整性
关系数据库中每个元组应该是可区分的,是唯一的。这样的约束条件用实体完整性来保证。
实体完整性规则:若属性(指一个或一组属性)A 是基本关系 R 的主属性则 A 不能取空值(nullvalue)。所谓空值就是“不知道”或“不存在”或“无意义”的值
按照实体完整性规则的规定,如果主码由若干属性组成,则所有这些主属性都不能取空值。
例如, 选修 ( 学号,课程号,成绩 ) 选修(学号,课程号,成绩) 选修(学号,课程号,成绩) 关系中, 学号、课程号 学号、课程号 学号、课程号 为主码,则 学号 学号 学号 和 课程号 课程号 课程号 两个属性都不能取空值
对于实体完整性规则说明如下:
-
实体完整性规则是针对基本关系而言的。一个基本表通常对应现实世界的一个实体集。例如学生关系对应于学生的集合。
-
现实世界中的实体是可区分的,即它们具有某种唯一性标识。例如每个学生都是独立的个体,是不一样的。
-
相应地,关系模型中以主码作为唯一性标识。
-
主码中的属性即主属性不能取空值。如果主属性取空值,就说明存在某个不可标识的实体,即存在不可区分的实体,这与第 2 点相矛盾,因此这个规则称为实体完整性。
参照完整性
为给出给出表达关系之间相互引用约束的参照完整性的定义,我们先引入外码的概念。
外码
设 F F F 是基本关系 R R R 的一个或一组属性,但不是关系 R R R 的码, K K K 是基本关系 S S S 的主码。如果 F F F 与 K K K 相对应,则称 F F F 是 R R R 的外码(foreign key),并称基本关系 R R R 为参照关系(referencing relation),基本关系 S S S 为被参照关系(referenced relation)或目标关系(targetrelation。关系 R R R 和 S S S 不一定是不同的关系。
目标关系 S S S 的主码 K K K 和参照关系 R R R 的外码 F F F 必须定义在同一个(或同一组)域上。
外码并不一定要与相应的主码同名,但在实际应用中为了便于识别,当外码与相应的主码属于不同关系时,往往给它们取相同的名字。
参照完整性规则
参照完整性规则就是定义外码与主码之间的引用规则:若属性(或属性组) F F F 是基本关系 R R R 的外码,它与基本关系 S S S 的主码 K K K 相对应(基本关系 R R R 和 S S S 不一定是不同的关系),则对于 R R R 中每个元组在 F F F 上的值必须:
取空值( F F F 的每个属性值均为空值) 或 等于 S S S 中某个元组的主码值。
用户自定义完整性
不同的关系数据库系统根据其应用环境的不同,往往还需要一些特殊的约束条件。用户定义的完整性就是针对某一具体关系数据库的约束条件,它反映某一具体应用所涉及的数据必须满足的语义要求。
-
例如某个属性必须取唯一值、某个非主属性不能取空值等。
-
例如,在学生关系中,若按照应用的要求学生不能没有姓名,则可以定义学生姓名不能取空值;某个属性(如学生的成绩)的取值范围可以定义在 0 ~ 100之间等。
关系模型应提供定义和检验用户自定义完整性的机制,以便用统一的系统的方法处理它们,而不需由应用程序承担这一功能。
关系数据规范化
根据属性间依赖情况来判定关系是否具有某些不合适的性质,通常按属性间依赖情况来区分关系规范化程度为 第一范式(1NF)、第二范式(2NF)、第三范式(3NF)和 第四范式(4NF)等,然后直观地描述如何将具有不合适性质的关系转换为更合适的形式。
规范化的基本思想是逐步消除数据依赖中不合适的部分,使模式中的各关系模式达到某种程度的“分离”,即“一事一地”的模式设计原则。
让一个关系描述一个概念、一个实体或者实体间的一种联系。若多于一个概念就把它“分离”出去。因此所谓规范化实质上是概念的单一化
关系模式的规范化过程是通过对关系模式的分解来实现的,即把低一级的关系模式分解为若干个高一级的关系模式。这种分解不是唯一的。
不遵循关系数据理论导致的问题
假设有一学校教务的数据库:学号(Sno)、所在系(Sdept)、 系主任姓名(Mname)、课程号(Cno)和成绩(Grade)。假设用一个单一的关系模式Student来表示,则该关系模式的属性集合为
U = ( S n o , S d e p t , M n a m e , C n o , G r a d e ) U=({Sno,Sdept,Mname,Cno,Grade}) U=(Sno,Sdept,Mname,Cno,Grade)
根据实际意义,有如下函数依赖:
F = ( S n o → S d e p t , S d e p t → M n a m e , ( S n o , C n o ) → G r a d e ) F=(Sno\to Sdept, Sdept\to Mname,(Sno,Cno)\to Grade) F=(Sno→Sdept,Sdept→Mname,(Sno,Cno)→Grade)
这样的关系模式是失败的,因为它存在以下问题
-
数据冗余:比如,每一个系的系主任姓名重复出现,重复次数与该系所有学生的所有课程成绩出现次数相同,这将浪费大量的存储空间
-
更新异常:比如,某系更换系主任后,必须修改与该系学生有关的每一个元组
-
插入异常:插入的数据不能被插入。如果一个系刚成立,尚无学生,则无法把这个系及其系主任的信息存入数据库
-
删除异常:不该被删除的数据被删除。如果某个系的学生全部毕业了,则在删除该系学生信息的同时,这个系及其系主任的信息也丢掉了
为了避免上述异常,需要引入关系数据规范化
数据依赖
数据依赖是一个关系内部属性与属性之间的一种约束关系。这种约束关系是通过属性间值的相等与否体现出来的数据间相关联系。它是现实世界属性间相互联系的抽象,是数据内在的性质,是语义的体现。
人们已经提出了许多种类型的数据依赖,其中最重要的是:函数依赖(FunctionalDependency,FD) 和 多值依赖(Multi-Valued Dependency,MVD)
函数依赖
函数依赖:如果 X X X 能确定 Y Y Y(或者说 Y Y Y 依赖 X X X,记作 X → Y X \to Y X→Y)那么就不可能存在两个元组,在 X X X 相同时 Y Y Y 却不同。
属性间的函数依赖关系类似于数学中的函数 y = f ( x ) y=f(x) y=f(x),自变量 x x x 确定之后,相应的函数值 y y y 也就唯一地确定了。函数依赖和别的数据依赖一样是语义范畴的概念,只能根据语义或者设计者对现实世界做强制性规定来确定一个函数依赖。
函数依赖极为普遍地存在于现实生活中。比如描述一个学生的关系,可以有学号(Sno)、姓名(Sname)、系名(Sdept)等几个属性。由于一个学号只对应一个学生,一个学生只在一个系学习。因而当 Sno 值确定之后,Sname 及所在系的 Sdept 也就被唯一地确定了。
类似的有 S n a m e = f ( S n o ) Sname=f(Sno) Sname=f(Sno), S d e p t = f ( S n o ) Sdept=f(Sno) Sdept=f(Sno):
-
Sno 函数决定 Sname,Sno函数决定Sdept
-
Sname 和 Sdept 函数依赖于 Sno
-
记作 S n o → S n a m e Sno \to Sname Sno→Sname S n o → S d e p t Sno \to Sdept Sno→Sdept
-
若 X → Y X\to Y X→Y,则称 X 是这个函数依赖的决定属性组,也称为决定因素(determinant)
-
若 X → Y X\to Y X→Y , Y → X Y\to X Y→X ,则记作 X ← → Y X\gets \to Y X←→Y
-
若 Y 不函数依赖于 X,则记作 X ↛ Y X\nrightarrow Y X↛Y
平凡函数依赖
定义:若 X → Y X\to Y X→Y,且 Y ⊆ X Y\subseteq X Y⊆X,则称 X → Y X\to Y X→Y 是平凡的函数依赖
如果 X 确定 Y,Y 是 X 的子集,那么则称 X 是 Y 的平凡函数依赖
如: ( S n o , C n o ) → S n o (Sno,Cno) \to Sno (Sno,Cno)→Sno
对于任意关系模式,平凡函数依赖都是必然成立的,它不反应新的语义
非平凡函数依赖
定义:若 X → Y X\to Y X→Y,但 Y ⊈ X Y\nsubseteq X Y⊈X,则称 X → Y X\to Y X→Y 是非平凡的函数依赖
即,如果 X 确定 Y,但 Y 并不是 X 的子集,那么则称 X 是 Y 的非平凡函数依赖
如: ( S n o , C n o ) → G r a d e (Sno,Cno) \to Grade (Sno,Cno)→Grade
完全函数依赖
定义:在 R ( U ) R(U) R(U) 中,若 X → Y X \to Y X→Y,并且对于 X X X 中的任意真子集 X ′ X^\prime X′,都有 X ′ ↛ Y X^\prime \nrightarrow Y X′↛Y,则称 Y 对 X 完全函数依赖,记作 X ⟶ F Y X\stackrel{F}{\longrightarrow} Y X⟶FY
部分函数依赖
定义:若 X → Y X\to Y X→Y ,且 Y Y Y 不完全函数依赖于 X X X,则称 Y 对 X 部分函数依赖,记作 X ⟶ P Y X\stackrel{P}{\longrightarrow}Y X⟶PY
传递依赖
定义:在 R ( U ) R(U) R(U) 中,若 X → Y X \to Y X→Y( Y ⊈ X Y\nsubseteq X Y⊈X), Y ↛ X Y\nrightarrow X Y↛X, Y → Z Y\to Z Y→Z, Z ⊈ Y Z\nsubseteq Y Z⊈Y,则称 Z 对 X 传递函数依赖,记作 X ⟶ 传递 Z X\stackrel{传递}{\longrightarrow}Z X⟶传递Z
如果 X 是 Y 的非平凡函数依赖,且 Y 不是 X 的函数依赖,同时 Y 是 Z 的非平凡函数依赖,则称 Z 对 X 传递函数依赖
直接函数依赖
定义:在 R ( U ) R(U) R(U) 中,若 X → Y X \to Y X→Y( Y ⊈ X Y\nsubseteq X Y⊈X), Y → X Y\rightarrow X Y→X, Y → Z Y\to Z Y→Z, Z ⊈ Y Z\nsubseteq Y Z⊈Y,则称 Z 对 X 直接函数依赖,记作 X ⟶ 直接 Z X\stackrel{直接}{\longrightarrow}Z X⟶直接Z
如果 X 是 Y 的非平凡函数依赖,且 Y 是 X 的函数依赖,同时 Y 是 Z 的非平凡函数依赖,则称 Z 对 X 传递函数依赖
如: S n o → S d e p t Sno\to Sdept Sno→Sdept, S d e p t → M n a m e Sdept\to Mname Sdept→Mname,则 S n o ⟶ 传递 M n a m e Sno\stackrel{传递}{\longrightarrow}Mname Sno⟶传递Mname
多值依赖
多值依赖(Multi-Valued Dependency,MVD)是数据库中的一个概念,用于描述关系模式中属性之间的依赖关系。
描述性定义:设 R ( U ) R(U) R(U) 是属性集 U U U 上的一个关系模式, X , Y , Z X,Y,Z X,Y,Z 是 U U U 的子集,并且 Z = U − X − Y Z = U-X-Y Z=U−X−Y,关系模式 R ( U ) R(U) R(U) 中多值依赖 X → → Y X \to \to Y X→→Y 成立,当且仅当 R ( U ) R(U) R(U) 的任一关系 r r r,给定的一对(X,Z),有一组 Y Y Y 的值,仅仅决定于 X X X 值,而与 Z Z Z 值无关
形式化定义:设 R ( U ) R(U) R(U) 是属性集 U U U 上的一个关系模式, X , Y , Z X,Y,Z X,Y,Z 是 U U U 的子集,并且 Z = U − X − Y Z = U-X-Y Z=U−X−Y,在 R ( U ) R(U) R(U) 的任一关系 r r r 中,如果存在 ( x , y 1 , z 1 ) (x,y_1,z_1) (x,y1,z1) 和 ( x , y 2 , z 2 ) (x,y_2,z_2) (x,y2,z2),即交换两个元组的 Y Y Y 值所得两个新元组 ( x , y 2 , z 1 ) (x,y_2,z_1) (x,y2,z1) 和 ( x , y 1 , z 2 ) (x,y_1,z_2) (x,y1,z2) 必在 r r r 中,那么就称 Y Y Y 多值依赖于 X X X,记作 X → → Y X \to \to Y X→→Y
在关系模式中,如果存在一个或多个属性组 X 可以决定另一个属性组 Y 的值,而不管 X 的其他属性的值如何改变,Y 的值始终保持不变,那么就存在一个多值依赖
多值依赖的性质:
X → → Y X \to \to Y X→→Y
-
对称性:若 X → → Y X \to \to Y X→→Y , Z = U − X − Y Z = U-X-Y Z=U−X−Y,则 X → → Z X \to \to Z X→→Z
-
传递性:若 X → → Y X \to \to Y X→→Y , Y → → Z Y \to \to Z Y→→Z,则 X → → Z − Y X \to \to Z-Y X→→Z−Y
-
函数依赖可以看作是多值依赖的特殊情况:若 X → Y X\to Y X→Y,则 X → → Y X \to \to Y X→→Y
是因为当 X → Y X\to Y X→Y 时,对 X 的每一个值 x,Y 有一个确定的值 y 与之对应
等价的多值依赖
等价的多值依赖(Equivalence MVD):当一个关系模式的两个属性组 X 和 Y 之间存在多值依赖时,如果 X 和 Y 是等价的,即关系模式中的两个实例满足 X → Y 和 Y → X,那么这个多值依赖就是等价的。
例如,如果在一个关系模式中,属性组 X 和 Y 互相依赖并且满足 X → Y 和 Y → X,那么就存在一个等价的多值依赖。
非等价的多值依赖
非等价的多值依赖(Non-Equivalence MVD):当一个关系模式的两个属性组 X 和 Y 之间存在多值依赖时,如果 X 和 Y 不是等价的,即关系模式中的两个实例满足 X → Y,但不满足 Y → X,那么这个多值依赖就是非等价的。
例如,在一个关系模式中,属性组 X 和 Y 存在多值依赖 X → Y,但不存在 Y → X。
平凡的多值依赖
若 X → → Y X \to \to Y X→→Y,而 Z = ∅ Z = \varnothing Z=∅ ,Z 为空,则称 X → → Y X \to \to Y X→→Y 为平凡的多值依赖。
即对于 R ( X , Y ) R(X,Y) R(X,Y) ,如果有 X → → Y X \to \to Y X→→Y 成立,则 X → → Y X \to \to Y X→→Y 为平凡的多值依赖
非平凡的多值依赖
若 X → → Y X \to \to Y X→→Y,而 Z ≠ ∅ Z \ne \varnothing Z=∅ ,则称 X → → Y X \to \to Y X→→Y 为非平凡的多值依赖。
范式
为解决数据不规范引起的异常问题,提出了范式(Normal Form)理论。
关系数据库中的关系是要满足一定要求的,满足不同程度要求的为不同范式。满足最低要求的叫第一范式,简称 1NF;在第一范式中满足进一步要求的为第二范式(2NF),其余以此类推。
范式概念可以理解成符合某一种级别的关系模式的集合,即 R 为第几范式就可以写成
R
∈
X
N
F
R\in_XNF
R∈XNF。(N 代表第 N 范式)
对于各种范式之间的关系有
5
N
F
⊂
4
N
F
⊂
B
C
N
F
⊂
3
N
F
⊂
2
N
F
⊂
1
N
F
5NF\subset 4NF\subset BCNF \subset 3NF \subset 2NF\subset 1NF
5NF⊂4NF⊂BCNF⊂3NF⊂2NF⊂1NF
规范化(normalization):一个低一级范式的关系模式通过模式分解(schemadecomposition)可以转换为若干个高一级范式的关系模式的集合。
1NF
在第一范式中,属性(对应于表中的字段)不可再分,也就是这个字段只能是一个值,不能再分为多个其他的字段了。1NF 是所有关系型数据库的最基本要求 ,也就是说关系型数据库中创建的表一定满足第一范式。
1NF 可能存在的如下问题:
- 插入异常
- 删除异常
- 更新异常
2NF
定义:若 R ∈ 1 N F R\in 1NF R∈1NF,且每一个非主属性都完全函数依赖于任何一个候选码,则 R ∈ 2 N F R\in 2NF R∈2NF。
2NF 在 1NF 的基础之上,消除了非主属性对于码的部分函数依赖。直观的看,就是一个表中只能保存同一种关系的数据,不能把多种数据保存在同一张表中。
但由于 2NF 的属性可能存在传递函数依赖,仍会导致插入异常、删除异常、修改异常的问题。
3NF
定义:若关系模式 R < U , F > ∈ 1 N F R<U,F>\in 1NF R<U,F>∈1NF 中不存在码 X,属性组 Y,以及非属性组 Z( Z ⊈ Y ) Z \nsubseteq Y) Z⊈Y),使得 X → Y X\to Y X→Y, Y → Z Y\to Z Y→Z 成立, Y ↛ X Y \nrightarrow X Y↛X,则称 R < U , F > ∈ 3 N F R<U,F>\in 3NF R<U,F>∈3NF
在第三范式中,每一个非主属性既不传递依赖于码,也不部分依赖于码。直观来看,表中的每一列数据都和主码直接相关,而不是间接相关。
3NF 在 2NF 的基础之上,消除了非主属性对于码的传递函数依赖 。符合 3NF 要求的数据库设计,基本上解决了数据冗余过大,插入异常,修改异常,删除异常的问题。但是在一些特殊情况下,仍然会产生一些异常情况和数据冗余。
BCNF
BCNF(Boyce Codd Normal Form)是由 Boyce 与 Codd 提出的,比上述的 3NF 又进了一步,通常认为 BCNF 是修正的第三范式,有时也称为扩充的第三范式。
定义:若关系模式 R < U , F > ∈ 1 N F R<U,F>\in 1NF R<U,F>∈1NF,若 X → Y X\to Y X→Y 且 Y ⊈ X Y\nsubseteq X Y⊈X 时 X X X 必含有码(即每一个决定因素都包含码),则 R < U , F > ∈ B C N F R<U,F>\in BCNF R<U,F>∈BCNF
一个满足 BCNF 的关系模式有:
-
所有非主属性对每一个码都是完全函数依赖。
-
所有主属性对每一个不包含它的码也是完全函数依赖
-
没有任何属性完全函数依赖于非码的任何一组属性。
4NF
关系模式 R < U , F > ∈ 1 N F R<U,F>\in 1NF R<U,F>∈1NF,如果对于 R R R 的每个非平凡函数依赖 X → → Y X \to \to Y X→→Y ( Y ⊈ X Y\nsubseteq X Y⊈X), X X X 都含有码,则称 R < U , F > ∈ 4 N F R<U,F>\in 4NF R<U,F>∈4NF
4NF 就是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。对于每一个非平凡的多值依赖 X → → Y X \to \to Y X→→Y, X X X 都含有候选码,于是就有 X → Y X\to Y X→Y,所以 4NF 所允许的非平凡的多值依赖实际上是函数依赖。
总结
关系型数据库广泛应用于各种需要高效数据存储和查询的场景中,如企业信息管理系统、电子商务系统、金融系统等。在这些系统中,关系型数据库能够高效地处理大量的数据查询、统计和并发读写操作,为系统的稳定运行提供有力支持。
关系型数据库以其结构化的存储方式、数据高一致性和共享性、丰富的安全控制机制以及广泛的应用场景,成为了数据库领域的重要组成部分。随着技术的不断发展,关系型数据库也在不断地演进和完善,以更好地满足各种复杂的应用需求。
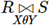
![![[Relational Data Language.png]]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9kaXJlY3QvOWVkNDhhOGViMWYxNDk0MzgxYTlkMzM3MmQwMDAwZTMucG5n)
![![[Forein Reference.png]]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9kaXJlY3QvZmFlNGVkNTAwNmNmNDY0ZjlhNjY0YTkzNGMzOTM0ZDQucG5n)
![![[Database Normal Form Layer.png]]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9kaXJlY3QvZWQ1MWFmYzc4ZWUwNGVkZTlkMTVlNTA0YzJjNTNkZWMucG5n)
![![[2NF Table.png]]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9kaXJlY3QvOGM5YmU3NDc0NmJmNGY3MjhlYzU2ZmYwOTA1NDZjNjAucG5n)