一、卡尔曼滤波的定义
卡尔曼滤波(Kalman Filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。该算法由鲁道夫·卡尔曼(Rudolf E. Kalman)在1960年提出,是一种基于最小均方误差准则的最优估计方法。其核心思想在于通过结合预测值和测量值,赋予更可靠的信息更高的权重,从而得到系统状态的最优估计。
卡尔曼滤波假设系统是线性的,并且噪声是高斯分布的。它适用于线性、离散和有限维系统。在卡尔曼滤波的过程中,系统状态通过预测和更新两个步骤进行迭代估计。预测步骤根据当前状态估计和控制输入,预测下一个时刻的状态和不确定性;更新步骤则结合测量值更新状态估计,并通过计算卡尔曼增益来平衡预测值和测量值的权重。
二、卡尔曼滤波的主要应用
卡尔曼滤波因其递归性和实时处理数据的能力,在众多领域得到了广泛的应用。以下是一些主要的应用场景:
- 导航和定位:
- GPS导航:卡尔曼滤波能够结合GPS信号和其他传感器数据(如加速度计、陀螺仪等),提供更准确的位置和速度估计。这在车辆导航、无人机飞行控制等场景中尤为重要。
- 飞机和导弹控制系统:通过融合多种传感器数据(如雷达、惯性导航系统等),卡尔曼滤波能够实时跟踪飞机的位置和速度,提高飞行控制的精度和稳定性。
- 金融领域:
- 股票价格预测:卡尔曼滤波可以用来平滑价格信号,估计价格趋势,为投资者提供决策支持。
- 波动率估计:在金融模型中,卡尔曼滤波可以用于估计市场波动率,帮助投资者评估市场风险。
- 信号处理:
- 音频和视频去噪:卡尔曼滤波能够滤除观测信号中的随机噪声,提高音频和视频的清晰度。
- 传感器数据融合:在多个传感器提供的数据存在噪声或不一致时,卡尔曼滤波能够融合这些数据,提供更可靠的状态估计。
- 控制系统:
- 机器人控制:卡尔曼滤波能够结合机器人的运动模型和传感器数据,实现精确的路径规划和运动控制。
- 自动驾驶:在自动驾驶系统中,卡尔曼滤波能够融合来自多个传感器的数据(如雷达、激光雷达、摄像头等),实时估计车辆的位置、速度和方向。
- 其他应用:
- 生物医学工程:在心电图分析、脑电波监测等领域,卡尔曼滤波能够用于信号处理和数据融合。
- 环境监测:在空气质量监测、水质监测等领域,卡尔曼滤波能够结合多个传感器的数据,提供更准确的环境参数估计。
三、卡尔曼滤波的基本原理
卡尔曼滤波的基本原理包括状态方程和观测方程、预测步骤和更新步骤、以及卡尔曼增益的计算。以下是对这些原理的详细介绍:
- 状态方程和观测方程:
- 状态方程:描述了系统状态随时间的演化规律。通常表示为 Xk=AXk−1+BUk+Wk,其中 Xk 是 k 时刻的系统状态,A 是状态转移矩阵,Uk 是控制输入,B 是控制矩阵,Wk 是过程噪声。
- 观测方程:描述了系统状态的观测值与真实值之间的关系。通常表示为 Zk=HXk+Vk,其中 Zk 是 k 时刻的观测值,H 是观测矩阵,Vk 是观测噪声。
- 预测步骤:
- 根据当前状态估计和控制输入,预测下一个时刻的状态和不确定性。预测状态表示为 X^k−=AX^k−1+BUk,其中 X^k− 是 k 时刻的先验状态估计,X^k−1 是 k−1 时刻的后验状态估计。预测误差协方差矩阵表示为 Pk−=APk−1AT+Q,其中 Pk−1 是 k−1 时刻的后验误差协方差矩阵,Q 是过程噪声的协方差矩阵。
- 更新步骤:
- 结合测量值更新状态估计。计算卡尔曼增益 Kk=Pk−HT(HPk−HT+R)−1,其中 R 是观测噪声的协方差矩阵。更新状态估计 X^k=X^k−+Kk(Zk−HX^k−),其中 Zk 是 k 时刻的观测值。更新误差协方差矩阵 Pk=(I−KkH)Pk−,其中 I 是单位矩阵。
四、MATLAB代码示例
以下是一个简单的MATLAB代码示例,用于演示卡尔曼滤波在位置和速度估计中的应用。假设一个物体以恒定速度运动,但存在过程噪声和观测噪声。我们将使用卡尔曼滤波来估计物体的位置和速度。
clc;
close all;
clear all;
warning off;
% 清除变量
rand('seed', 100);
randn('seed', 100);
format long g;
% 估计汽车在每个时刻的位置和速度
timemat = [1:1:30]'; % 离散时间序列(秒)
N = length(timemat);
v = 4; % 初始速度(未知实际值)
u = 0.2; % 加速度
nsmat = 10 * randn(N, 1); % GPS测量误差,标准差为10米
Z_ = zeros(N, 1);
v_ = v + (timemat-1)*u; % 实际速度值
for i = 2:N
Z_(i) = Z_(i-1) + v_(i-1) + 1/2*u; % 实际位置
end
% 已知量
Z = Z_ + nsmat; % GPS观测值,包含测量误差
Q = [1e-3 0; 0 1e-3]; % 过程噪声协方差矩阵,超参数
R = 1; % 观测噪声协方差矩阵,超参数(一维情况下为数值)
% 初始化
X = [0; 0]; % 初始状态,[位置, 速度],即要估计的量
P = [0.1 0; 0 0.1]; % 先验误差协方差矩阵的初始值,基于经验给出
% 已知线性变换矩阵
F = [1 1; 0 1]; % 状态转移矩阵
B = [1/2; 1]; % 控制矩阵
H = [1 0]; % 观测矩阵
% 每个时刻的状态记录
Xmat = zeros(size(X,1),N);
Xmat(:,1) = X;
for i = 1:N
X_ = F*X + B*u; % 估计新状态
P_ = F*P*F' + Q; % 更新协方差矩阵
K = P_*H' / (H*P_*H' + R); % 计算卡尔曼增益
X = X_ + K*(Z(i) - H*X_); % 根据估计值和观测值矫正更新预测值
P = (eye(2) - K*H)*P_; % 更新协方差矩阵
Xmat(:,i) = X; % 记录预测值
end
% 绘图
figure;
plot(timemat, Z_,'b.-'); hold on;
plot(timemat, Xmat(1, :), 'r*');
xlabel('Time'); ylabel('Position'); title('Estimate of Position');
grid on
figure;
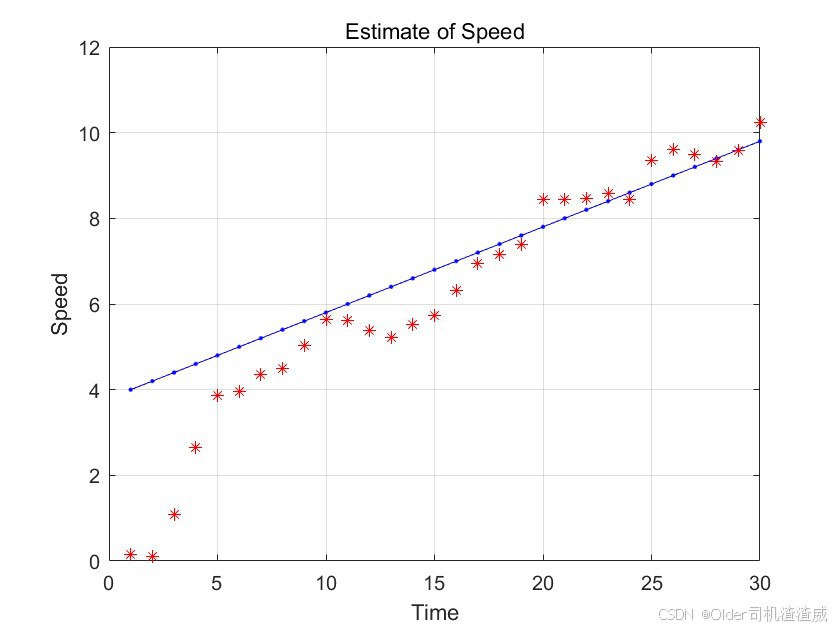
plot(timemat, v_,'b.-'); hold on;
plot(timemat, Xmat(2, :), 'r*');
grid on
xlabel('Time'); ylabel('Speed'); title('Estimate of Speed');
在这个示例中,我们首先初始化了系统参数和噪声矩阵。然后,我们根据物体的运动模型和观测数据,使用卡尔曼滤波算法迭代估计物体的位置和速度。最后,我们绘制了实际位置和速度与估计位置和速度的对比图,以验证卡尔曼滤波的效果。
五、总结与展望
卡尔曼滤波作为一种基于线性系统状态方程的最优估计方法,在导航、控制系统、信号处理、金融预测等多个领域得到了广泛的应用。其核心思想在于通过结合预测值和测量值,赋予更可靠的信息更高的权重,从而得到系统状态的最优估计。
随着技术的不断发展,卡尔曼滤波算法也在不断改进和扩展。例如,扩展卡尔曼滤波(Extended Kalman Filter, EKF)被用于处理非线性系统;无迹卡尔曼滤波(Unscented Kalman Filter, UKF)通过无迹变换来近似非线性系统的概率分布;粒子滤波(Particle Filter)则适用于非高斯噪声和非线性系统的状态估计。未来,卡尔曼滤波及其变种算法将在更多领域发挥重要作用,特别是在自动驾驶、机器人控制、生物医学工程