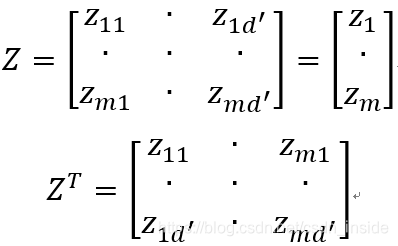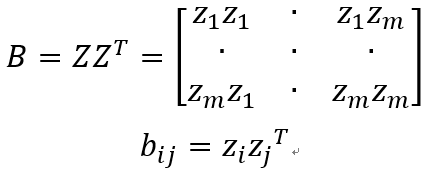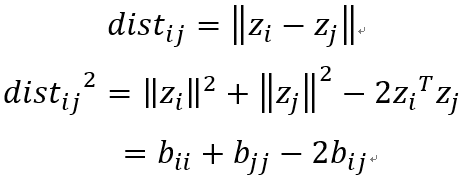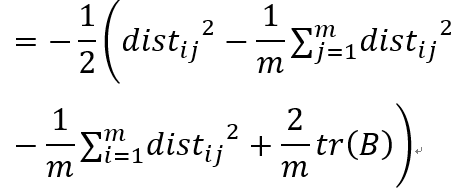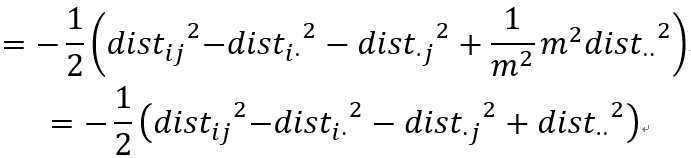MDS 降维详细推导及 Python实现

MDS的思路就是保持新空间与原空间的相对位置关系，先用原空间的距离矩阵D，求得新空间的内积矩阵B，再由内积矩阵B求得新空间的表示方法Z。

西瓜书上的推导比较简洁，自己详细的推了一遍。

假设Z矩阵是新空间的表示，mxd'维，z1，z2到zm表示一个行向量，即每一个样本。

定义新空间的内积矩阵B，B矩阵的bij元素，即是z的第i行与第j行的内积。

为了使新空间与原空间保持相对位置关系，新空间两个样本的距离要等于（或者约等于）原空间的距离。

为了便于讨论，这里使Z被中心化，即Z所有元素相加=0。

下面开始推导，对于里面的bij项，对i从1到m求和，j不动：

同理：

对于bii项，对的i从1到m求和，注意这里是对i求和，不对j求和，所以结果是mbjj：

···············①

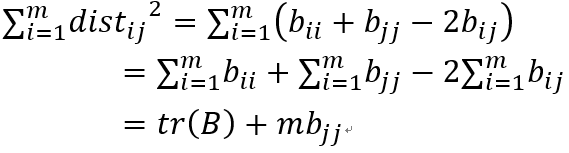
tr(B)表示B矩阵的迹，对角元素之和。

同理，对j求和：

················②

再用上式对i求和：

··················③

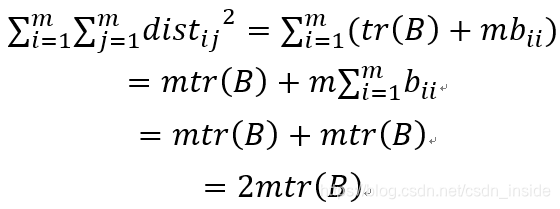
为了化简，令

··············④⑤⑥

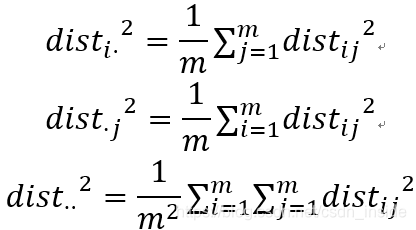
由①②式，移项可得：

················⑦⑧

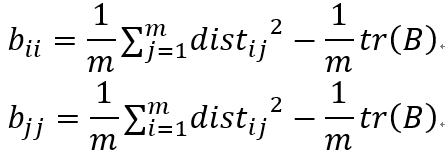
由③式，移项可得：

·····················⑨

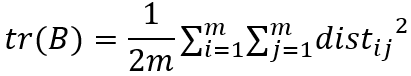
由

可得：

将⑦⑧式的bii和bjj带入上式，可得：

再由④⑤式带入，替换掉、，⑨带入替换掉tr(B)，可得：

最后由⑥化简最后一项得到：

这样就可以由原空间距离矩阵D求得内积矩阵B。

由于

其中Λ是特征值组成的对角阵，就可得到：

即用B求得Z。

代码+实战

import numpy as np
import matplotlib.pyplot as plt

class MyMDS:
    def __init__(self,n_components):
        self.n_components=n_components
    
    def fit(self,data):
        m,n=data.shape
        dist=np.zeros((m,m))
        disti=np.zeros(m)
        distj=np.zeros(m)
        B=np.zeros((m,m))
        for i in range(m):
            dist[i]=np.sum(np.square(data[i]-data),axis=1).reshape(1,m)
        for i in range(m):
            disti[i]=np.mean(dist[i,:])
            distj[i]=np.mean(dist[:,i])
        distij=np.mean(dist)
        for i in range(m):
            for j in range(m):
                B[i,j] = -0.5*(dist[i,j] - disti[i] - distj[j] + distij)
        lamda,V=np.linalg.eigh(B)
        index=np.argsort(-lamda)[:self.n_components]
        diag_lamda=np.sqrt(np.diag(-np.sort(-lamda)[:self.n_components]))
        V_selected=V[:,index]
        Z=V_selected.dot(diag_lamda)
        return Z

先用自己的MDS，然后用sklearn的MDS，可视化一下iris.data：

from sklearn.datasets import load_iris
iris=load_iris()

clf1=MyMDS(2)
iris_t1=clf1.fit(iris.data)
plt.scatter(iris_t1[:,0],iris_t1[:,1],c=iris.target)
plt.title('Using My MDS')

from sklearn.manifold import MDS
clf2=MDS(2)
clf2.fit(iris.data)
iris_t2=clf2.fit_transform(iris.data)
plt.scatter(iris_t2[:,0],iris_t2[:,1],c=iris.target)
plt.title('Using sklearn MDS')

降维的效果基本一致，对于紫色的花，都可以有效区分；对于绿色和黄色的花，有一些难以区分。

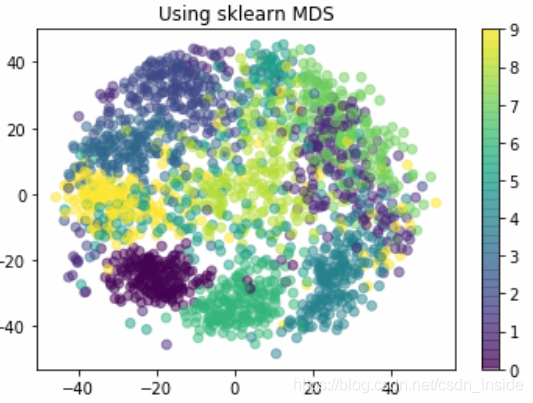
再对sklearn的digits数据降维可视化看一看：

from sklearn.datasets import load_digits
digits=load_digits()
clf3=MyMDS(2)
digits_t1=clf3.fit(digits.data)
plt.scatter(digits_t1[:,0],digits_t1[:,1],c=digits.target,
           alpha=.5)
plt.colorbar()
plt.title('Using My MDS')

from sklearn.manifold import MDS
mds=MDS(n_components=2)
mds.fit(digits.data)
digits_t2=mds.fit_transform(digits.data)
plt.scatter(digits_t2[:,0],digits_t2[:,1],c=digits.target,
            alpha=.5)
plt.colorbar()
plt.title('Using sklearn MDS')

from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca.fit(digits.data)
digits_t2=pca.fit_transform(digits.data)
plt.scatter(digits_t2[:,0],digits_t2[:,1],c=digits.target
           ,alpha=.5)
plt.colorbar()
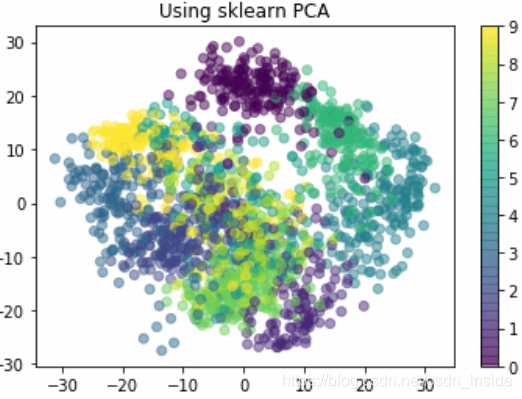
plt.title('Using sklearn PCA')

from sklearn.manifold import Isomap
iso=Isomap(n_components=2)
iso.fit(digits.data)
digits_projected=iso.transform(digits.data)
plt.scatter(digits_projected[:,0],digits_projected[:,1],c=digits.target
           ,alpha=.5)
plt.colorbar()
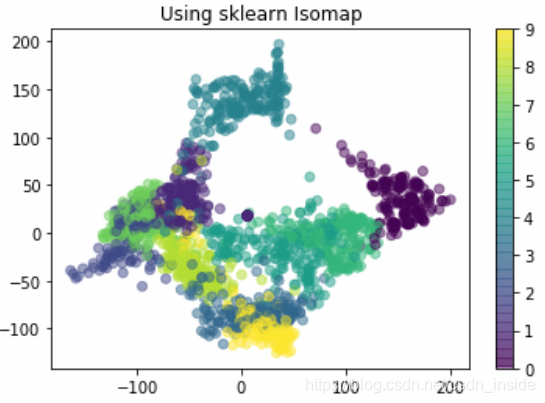
plt.title('Using sklearn Isomap')

sklearn的MDS跑了很久，不知道为何。。。

效果。。。三者小巫见大巫，都不是很好，有的数字难以区分。

所以换Isomap流形学习看看：

发现效果好比上述两种降维要一些，说明digits数据集的真实分布，不是线性的，更接近于流形，单纯的PCA和MDS不能很好的解决问题。

MDS 降维 详细推导 及 Python实现

悦读

MDS 降维详细推导及 Python实现