fpga深度学习gpu加速

去年三月，我在QCon-London上发表了有关TornadoVM的演讲，在其中我对TornadoVM进行了介绍并解释了其工作原理。 在本文中，我从QCon London演讲中进行了扩展，并展示了有关开发人员如何通过在异构硬件上自动运行Java来从中受益的更多详细信息。

首先，我将提供TornadoVM项目和体系结构的一般概述。 其次，我将通过一个实际的例子来说明TornadoVM的不同部分。

为什么我们需要类似TornadoVM的东西？

没有一种单一的计算机体系结构最适合有效地执行所有类型的工作负载。 近年来，这导致异构硬件的激增，这意味着我们编程的每个系统都可能包含多种计算元素。

这些元素中的每一个都有不同的硬件特性。 硬件的异构性使程序员能够在降低能耗的同时提高其应用程序的性能。

这些用于计算的新型异构设备包括多核CPU，图形处理单元（GPU）和现场可编程门阵列（FPGA）。 这种多样性很好，但是我们需要一种有效地对这些新设备进行编程的方法。

两种最受欢迎​​的异构编程语言CUDA和OpenCL就是一个典型的例子。 但是，它们在API中公开了一些低级功能，因此很难被非专业用户使用。 例如，我突出显示了以下来自OpenCL 3.0标准的引用：

OpenCL的目标是希望编写可移植但高效的代码的专业程序员。 [...]因此，OpenCL提供了底层硬件抽象以及支持编程的框架，并且公开了底层硬件的许多细节。

前面的声明也适用于CUDA和类似的并行编程模型。 在行业和学术界，开发人员倾向于使用高级的，面向对象的编程语言，而不是使用低级的编程语言，这些语言通常在托管的运行时环境（例如Java，R，Python和JavaScript）上执行。 尽管许多程序员可能希望这样的编程语言已经适合在异构硬件上透明地执行，但现实是它们的支持非常有限或根本没有。

在本文中，我们探索TornadoVM，它是用于异构计算的低级并行编程语言的替代方法。 我们将展示开发人员如何在无需任何有关并行计算体系结构或并行编程模型的知识的情况下使用多核CPU和GPU。

简而言之，TornadoVM是用于JVM语言的并行编程框架，可以透明且动态地将Java字节码卸载到OpenCL中，并在异构硬件上执行生成的代码。 此外，TornadoVM集成了优化的运行时，可以重新使用设备缓冲区并保存跨设备的数据传输，还集成了新颖的动态应用程序重新配置组件，可以在计算设备之间执行实时任务迁移。

让我们开始吧！

下图显示了TornadoVM项目的高级概述。 如我们所见，TornadoVM由分层的微内核软件体系结构组成，其中的核心组件是TornadoVM执行引擎。 在最高级别，TornadoVM向开发人员公开API。 这是因为TornadoVM当前未检测到并行性（自动并行化）。 相反，它利用并行性。 因此，TornadoVM需要一种方法来识别哪些方法或功能适合在GPU和FPGA上运行。

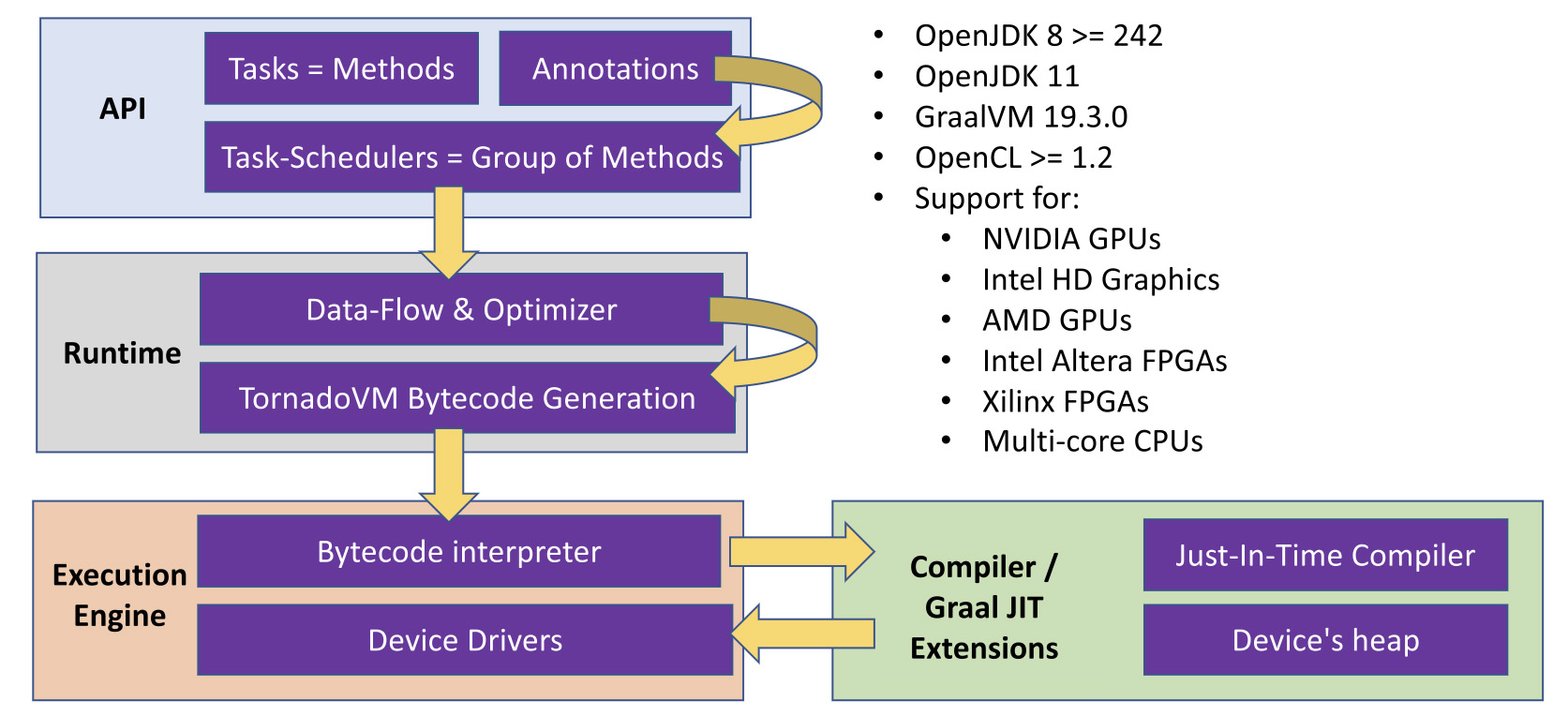
此外，TornadoVM包含一个核心运行时，该运行时分为几个组件：a）具有新字节码生成器的数据流优化器； b）一个小的字节码解释器来运行新的字节码，以及c）JIT编译器和内存管理。 在本文中，我将重点介绍API，运行时以及JIT编译器的一般概述。

最后，如上图所示，TornadoVM当前使用最新的JDK（u242）和JVMCI支持Java 8，并通过GraalVM 19.3.0支持OpenJDK 11。 TornadoVM还与OpenCL 1.2兼容，因此可以在多种设备上运行，例如GPU（AMD和NVIDIA），FPGA（Xilinx和Intel），集成GPU（例如Mali ARM和Intel HD Graphics）以及多核CPU。

实践中的TornadoVM

让我们通过一个实际的例子来详细介绍。 如下所示，我演示了如何在多核CPU，GPU和集成GPU上使用TornadoVM编程和运行矩阵乘法。 矩阵乘法是一个简单的代码，用于说明TornadoVM中的不同概念，它构成了许多机器学习和深度学习应用程序的核心。

注意：尽管TornadoVM是用Java编程的，但可以通过GraalVM（ Truffle ）的Polyglot编程框架将计算内核公开给其他JVM语言。

以下代码段显示了用Java编程的矩阵乘法：

class Compute { 
   public static void matrixMultiplication(final float[] A, final float[] B, final float[] C, final int size) { 
    	for (int i = 0; i < size; i++) { 
        	for (int j = 0; j < size; j++) { 
            	float sum = 0.0f; 
            	for (int k = 0; k < size; k++)  
                	sum += A[(i * size) + k] * B[(k * size) + j];