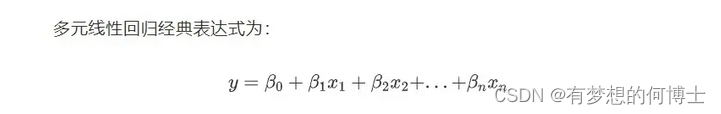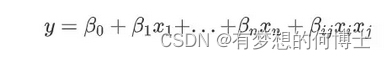说明

要在MATLAB中进行多元非线性回归，你需要定义一个非线性模型，然后使用该模型和你的数据进行回归分析。
以下是一个简化的示例，演示如何针对一个假定的非线性模型和虚构数据，这里有四个影响因子（自变量），一个因变量，我们以计算因子a、b、c、d的回归系数为例。

步骤如下:
首先导入数据
定义适合数据最佳的非线性模型，这一步可以提前采用非线性公式拟合线试试看谁更合适
这一步很关键，我会考虑后续出一期来专门讲这个，假设你手头有一组数据，如何确定最优的拟合关系式？
然后求解出对应变量的系数
检查模型的拟合优度或者其他统计信息是否拟合效果较好、通过显著性检验
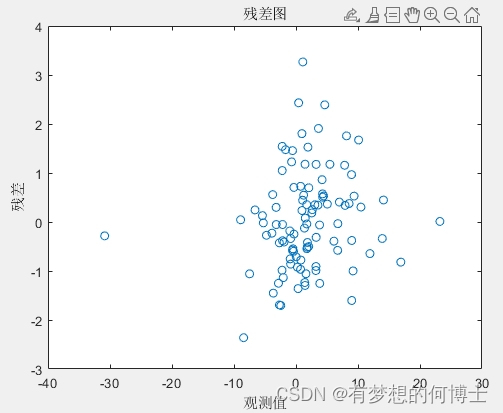
如果残差随机分布在零附近（没有明显的模式），则表明模型拟合良好。如果残差图显示出特定的模式，则可能表明模型中缺少重要变量或者模型形式不正确。当然模型拟合度也可以看看拟合优度指标（相关系数、均方根误差等）是否更优。

而非线性在上面的线性公式上变换，可以是如下的形式，也可以是高次（2次，3次等）的多种形式：

废话不多说，上代码

代码

代码如下：

clear all
clc
close all
% 假定的数据 - 在实际情况中，你需要替换这些数据为你的数据集
a = randn(100,1); % 因子a
b = randn(100,1); % 因子b
c = randn(100,1); % 因子c
d = randn(100,1); % 因子d
y = 2*a.^2 + 3*b + c.^3 - 0.5*d + randn(100,1); % 假定的因变量y，包含随机噪声

% 定义非线性模型
% 假定模型为 y = β1*a^2 + β2*b + β3*c^3 + β4*d + ε
%请注意这个关系式是假定的
% 其中ε是误差s项
modelFun = @(b,x)(b(1)*x(:,1).^2 + b(2)*x(:,2) + b(3)*x(:,3).^3 + b(4)*x(:,4));

% 初始参数估计
beta0 = [0,0,0,0]; % 初始猜测的系数值

% 进行非线性回归
X = [a b c d]; % 把因子组合在一起
[beta,R,J,CovB,MSE,ErrorModelInfo] = nlinfit(X, y, modelFun, beta0);

% 显示结果
fprintf('回归系数为:\nβ1(针对a^2) = %.2f\nβ2(针对b) = %.2f\nβ3(针对c^3) = %.2f\nβ4(针对d) = %.2f\n', beta);

% 如果你想检查模型的拟合优度或者其他统计信息，可以使用ErrorModelInfo和其他输出参数
% 计算参数的标准误差
SE = sqrt(diag(CovB));

% 打印参数的标准误差
fprintf('参数的标准误差为:\nβ1 = %.2f\nβ2 = %.2f\nβ3 = %.2f\nβ4 = %.2f\n', SE);

% 计算置信区间
alpha = 0.05; % 置信水平95%
CI = nlparci(beta,R,'jacobian',J,'alpha',alpha);

% 打印置信区间
fprintf('参数的95%%置信区间为:\nβ1: [%.2f, %.2f]\nβ2: [%.2f, %.2f]\nβ3: [%.2f, %.2f]\nβ4: [%.2f, %.2f]\n', CI');
% 绘制残差图
figure;
plot(y, R, '-o');
xlabel('观测值');
ylabel('残差');
title('残差图');

下面这段MATLAB代码实现了一个多元非线性回归模型，只需要拟合参数，具体包括以下步骤：

生成随机数据集 x、y、z，其中 z 是根据公式 z = 10 * exp(-x / 2) + 0.5 * y 生成的，同时加入了一定比例的噪声。
使用 lsqcurvefit 函数对数据进行最小二乘拟合，拟合模型为 z = w1 * exp(-x / w2) + w3 * y。
使用梯度下降法对数据进行学习，优化模型参数。实现了一个自定义的梯度下降优化，以迭代地调整参数 w1​、w2和 w3​。这种优化使用Adagrad方法，根据梯度的历史情况调整每个参数的学习率，使得处理不同规模的数据更加容易，并更可靠地收敛。被最小化的目标函数（成本函数）是观测和预测的 z 值之间的均方误差。
绘制学习过程中损失函数随迭代次数的变化曲线，以及拟合曲面与原始数据的对比图。
请注意，代码中的梯度下降法部分使用了 Adagrad 方法来更新学习率，并在迭代过程中记录了损失函数值的变化。绘图部分展示了损失函数曲线和拟合曲面与原始数据的关系。

% 清除环境变量和控制台输出，为运行准备环境
clear; clc;

% 定义模型 z = w1 * exp(-x / w2) + w3 * y
% 具体形式 z = 10 * exp(-x / 5) + 2 * y （作为示例）

% 初始化数据点数量和随机数生成器
len = 20;
rng('default');

% 生成随机x和y数据，范围在[0, len + 1] / 5
x = randi(len + 1, len, 1) / 5;
y = randi(len + 1, len, 1) / 5;

% 使用预设参数和生成的x,y计算z值
z = 10 * exp(-x / 2) + 0.5 * y;

% 添加随机噪声到z值中，增强模型的健壮性
ratio = 0.0; % 噪声比例设置为0，表示不添加噪声
z = z + ratio * max(z) * rand(len, 1);

% 准备拟合数据集
X = [x, y];

% 定义非线性模型函数
fun = @(var, X) var(1) * exp(-X(:, 1) / var(2)) + var(3) * X(:, 2);

% 使用lsqcurvefit拟合模型参数
initialParams = [1, 1, 1]; % 初始参数猜测
w = lsqcurvefit(fun, initialParams, X, z);
disp(['lsqcurvefit 计算结果：', num2str(w)]);

% 初始化梯度下降参数
alpha = 5; % 学习率
iteMax = 10000; % 最大迭代次数
initW = [1; 1; 1]; % 参数初始值
err = 1e-6; % 收敛阈值

% 初始化梯度下降过程的变量
J = zeros(iteMax, 1); % 存储每次迭代的损失
G = zeros(3, 1); % 用于Adagrad的累计梯度平方
e = 0.1; % Adagrad平滑项，避免除以0

% 开始梯度下降迭代
for i = 1 : iteMax
    % 计算梯度
    gradW1 = 1 / len * (exp(-x / initW(2)))' * (initW(1) * exp(-x / initW(2)) + initW(3) * y - z);
    gradW2 = 1 / len * (initW(1) * x .* exp(-x / initW(2)) / initW(2)^2)' * (initW(1) * exp(-x / initW(2)) + initW(3) * y - z);
    gradW3 = 1 / len * y' * (initW(1) * exp(-x / initW(2)) + initW(3) * y - z);
    grad = [gradW1; gradW2; gradW3];
    
    % 更新累计梯度平方（Adagrad）
    G = G + grad.^2;
    % 更新参数
    initW = initW - alpha * diag(1 ./ sqrt(G + e)) * grad;
    
    % 检查收敛性
    if norm(initW - initW) < err
        J(i + 1 : end) = []; % 裁剪多余的J值
        disp(['梯度下降法迭代次数：', num2str(i)]);
        disp(['梯度下降法计算结果：', num2str(initW')]);
        break;
    else
        % 计算并存储当前迭代的损失值
        J(i) = 1 / (2 * len) * (initW(1) * exp(-x / initW(2)) + initW(3) * y - z)' * (initW(1) * exp(-x / initW(2)) + initW(3) * y - z);
    end
end

% 绘制损失函数的收敛情况
subplot(1, 2, 1)
loglog(J, 'LineWidth', 2)
title('Cost Function Convergence')
xlabel('Iteration')
ylabel('Cost')
legend(['alpha = ', num2str(alpha)]);

% 绘制数据点和拟合结果
xFit = linspace(min(x), max(x), 30);
yFit = linspace(min(y), max(y), 30);
[xFitGrid, yFitGrid] = meshgrid(xFit, yFit);
zFit = initW(1) * exp(-xFitGrid / initW(2)) + initW(3) * yFitGrid;

subplot(1, 2, 2)
scatter3(x, y, z, 'filled');
hold on
mesh(xFitGrid, yFitGrid, zFit);
title('Data Points and Fitted Model')
xlabel('x')
ylabel('y')
zlabel('z')
legend('Data Points', 'Fitted Model', 'Location', 'NorthOutside');
hold off

如果需要更多关于数据特征分析方面等的代码（MATLAB和R语言）。也可关注我的专栏，纯粹博士期间日常研究干货分享。（代码可直接运行，包含注释和示例数据，替换数据即可运行出结果）
欢迎扫码关注公众号，获取更多代码和前沿论文资讯等相关内容

结果展示

首先能看出来每个系数的值与我们假定的2，3，1和-0.5系数很接近，其次从残差图可以看出来残差随机分布在零附近（没有明显的模式），证明模型的拟合优度不错，求解系数效果也不错。