实验名称:实验二、神经网络
一、实验目的
(1)掌握神经网络的 BP 算法原理与实现方法;
(2)神经网络的构建、训练和测试方法。
二、实验内容
(1)BP算法
使用 Python 语言编程实现标准 BP 算法和累积 BP 算法,在 wine 数据集(wine_data.csv)上分别使用这两个算法训练一个单隐层网络(如,13×100×3),并进行比较。要求:
1)学习率 e 在[0.001, 0.5]内,分析 e 的大小对算法性能的影响;
2)绘制均方误差随训练轮数的变化曲线;
3)改变隐层神经元的个数,观察网络的性能,进行分析;
4)输出混淆矩阵和准确率。
说明:
1)wine 数据集的最后一列为 wine 的类别;
2)建议标准 BP 算法的学习率 e 选在[0.001, 0.1]内,使用试错法选出合适值;
3)建议累积 BP 算法的学习率 e 选在[0.05, 0.5]内,使用试错法选出合适值,设置适当的循环轮数。
(2)TensorFlow使用
使用 TensorFlow(或 Pytorch)建立一个 4 层神经网络(如,13×16×50×10×3),对 wine 数据集(wine_data.csv)进行分类。要求:
1)学习率 e 在[0.001, 0.01]内;
2)绘制均方误差、准确率随训练轮数的变化曲线;
3)改变隐层神经元的个数,观察网络的性能,进行分析;
4)(选做)从训练数据集中留出一部分测试数据,进行验证,输出混淆矩阵和准确率。
三、实验代码和过程
(1)bp算法
1)导包
import seaborn as sn
import pandas as pd
import numpy as np
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
2)设置随机种子
seed = 2022
import random
np.random.seed(seed) # Numpy module.
random.seed(seed) # Python random module.
3)归一化
def preprocess(data):
ss = StandardScaler()
X = data.drop('class',axis='columns')
Y = data['class']
# print(Y[0])
X = ss.fit_transform(X)
x,y = np.array(X),np.array(Y).reshape(Y.shape[0],1)
return x,y
4)累积BP算法
def accumulate_BP(x,y,dim=10,eta=0.1,max_iter=1000):
n_samples = x.shape[0]
w1 = np.zeros((x.shape[1],dim))
b1 = np.zeros((n_samples,dim))
w2 = np.zeros((dim,1))
b2 = np.zeros((n_samples,1))
losslist = []
for ite in range(max_iter):
##前向传播
u1 = np.dot(x,w1)+b1
out1 = sigmoid(u1)
u2 = np.dot(out1,w2)+b2
out2 = sigmoid(u2)
loss = np.mean(np.square(y - out2))/2
losslist.append(loss)
print('iter:%d loss:%.4f'%(ite,loss))
##反向传播
##标准BP
d_out2 = -(y - out2)
d_u2 = d_out2*d_sigmoid(out2)
d_w2 = np.dot(np.transpose(out1),d_u2)
d_b2 = d_u2
d_out1 = np.dot(d_u2,np.transpose(w2))
d_u1 = d_out1*d_sigmoid(out1)
d_w1 = np.dot(np.transpose(x),d_u1)
d_b1 = d_u1
##更新
w1 = w1 - eta*d_w1
w2 = w2 - eta*d_w2
b1 = b1 - eta*d_b1
b2 = b2 - eta*d_b2
##Loss可视化
plt.figure()
plt.plot([i+1 for i in range(max_iter)],losslist)
plt.legend(['accumlated BP'])
plt.xlabel('iteration')
plt.ylabel('loss')
plt.show()
return w1,w2,b1,b2
5)标准BP算法
def standard_BP(x,y,dim=100,eta=0.1,max_iter=500):
n_samples = 1
w1 = np.zeros((x.shape[1],dim))
b1 = np.zeros((n_samples,dim))
w2 = np.zeros((dim,1))
b2 = np.zeros((n_samples,1))
losslist = []
for ite in range(max_iter):
loss_per_ite = []
for m in range(x.shape[0]):
xi,yi = x[m,:],y[m,:]
xi,yi = xi.reshape(1,xi.shape[0]),yi.reshape(1,yi.shape[0])
##前向传播
u1 = np.dot(xi,w1)+b1
out1 = sigmoid(u1)
u2 = np.dot(out1,w2)+b2
out2 = sigmoid(u2)
loss = np.square(yi - out2)/2
loss_per_ite.append(loss)
print('iter:%d loss:%.4f'%(ite,loss))
##反向传播
##标准BP
d_out2 = -(yi - out2)
d_u2 = d_out2*d_sigmoid(out2)
d_w2 = np.dot(np.transpose(out1),d_u2)
d_b2 = d_u2
d_out1 = np.dot(d_u2,np.transpose(w2))
d_u1 = d_out1*d_sigmoid(out1)
d_w1 = np.dot(np.transpose(xi),d_u1)
d_b1 = d_u1
##更新
w1 = w1 - eta*d_w1
w2 = w2 - eta*d_w2
b1 = b1 - eta*d_b1
b2 = b2 - eta*d_b2
losslist.append(np.mean(loss_per_ite))
##Loss可视化
plt.figure()
plt.plot([i+1 for i in range(max_iter)],losslist)
plt.legend(['standard BP'])
plt.xlabel('iteration')
plt.ylabel('loss')
plt.show()
return w1,w2,b1,b2
5)测试
u1 = np.dot(x,w1)+b1
out1 = sigmoid(u1)
u2 = np.dot(out1,w2)+b2
out2 = sigmoid(u2)
# print(out2)
y_pred = np.round(out2)
# print(y_pred)
result = pd.DataFrame(np.hstack((y,y_pred)),columns=['真值','预测'] )
result.to_excel('result_numpy.xlsx',index=False)
(2)TF使用
1)导包
import os
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
from keras import layers
2)数据处理
data_num = data.shape[0]
indexes = np.random.permutation(data_num)
train_indexes = indexes[:int(data_num * 0.6)]
val_indexes = indexes[int(data_num * 0.6):int(data_num * 0.8)]
test_indexes = indexes[int(data_num * 0.8):]
train_data = data.loc[train_indexes]
val_data = data.loc[val_indexes]
test_data = data.loc[test_indexes]
train_validation_data = pd.concat([train_data, val_data])
mean = train_validation_data.mean()
std = train_validation_data.std()
train_data = (train_data - mean) / std
val_data = (val_data - mean) / std
x_train = np.array(train_data.drop('class', axis='columns'))
y_train = np.array(train_data['class'])
x_val = np.array(val_data.drop('class', axis='columns'))
y_val = np.array(val_data['class'])
3)构建神经网络训练
model = keras.Sequential(name = 'model-1')
model.add(layers.Dense(16, activation='relu', input_shape=(13,)))
model.add(layers.Dense(50, activation='relu'))
model.add(layers.Dense(10, activation='relu'))
model.add(layers.Dense(3))
model.summary()
model.compile(keras.optimizers.Adam(0.001),
loss=keras.losses.MeanSquaredError(),
metrics=[keras.metrics.MeanAbsoluteError()])
history = model.fit(x_train, y_train,
batch_size = 64,
epochs = 300,
validation_data = (x_val, y_val),
)
4)绘制曲线
# 绘制曲线
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
lns1 = ax1.plot(np.arange(1000), fig_loss, label="Loss")
# 按一定间隔显示实现方法
# ax2.plot(200 * np.arange(len(fig_accuracy)), fig_accuracy, 'r')
lns2 = ax2.plot(np.arange(1000), fig_accuracy, 'r', label="Accuracy")
ax1.set_xlabel('iteration')
ax1.set_ylabel('training loss')
ax2.set_ylabel('training accuracy')
# 合并图例
lns = lns1 + lns2
labels = ["Loss", "Accuracy"]
# labels = [l.get_label() for l in lns]
plt.legend(lns, labels, loc=7)
plt.show()
四、实验结果截图及结果分析
(1)BP算法
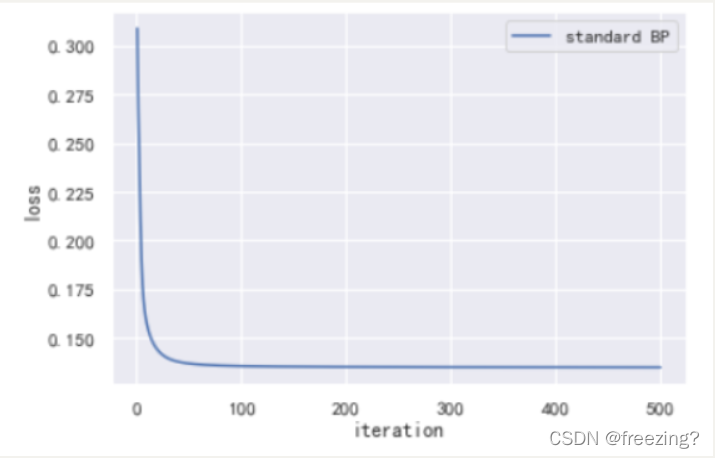
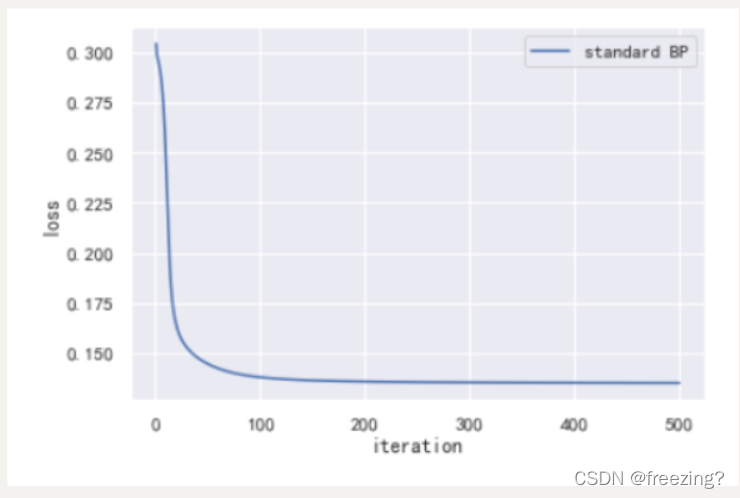
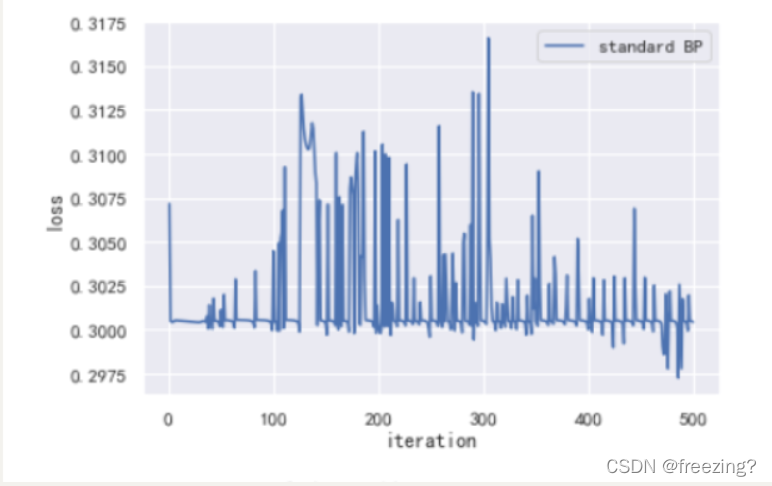
1)标准BP算法
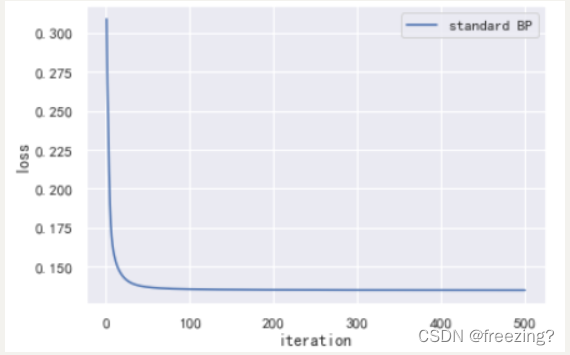
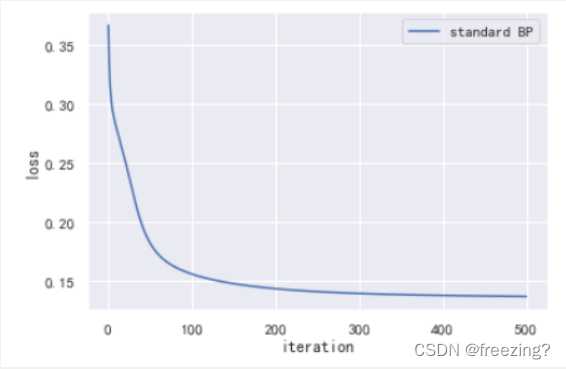
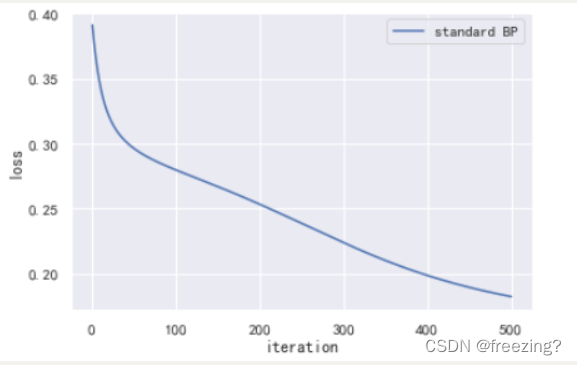
1、研究学习率
学习率0.1
学习率0.01
学习率0.001
分析:在迭代次数为500次,隐藏层为10的前提下,提高学习率可以加快损失值的下降收敛,提高算法的性能。
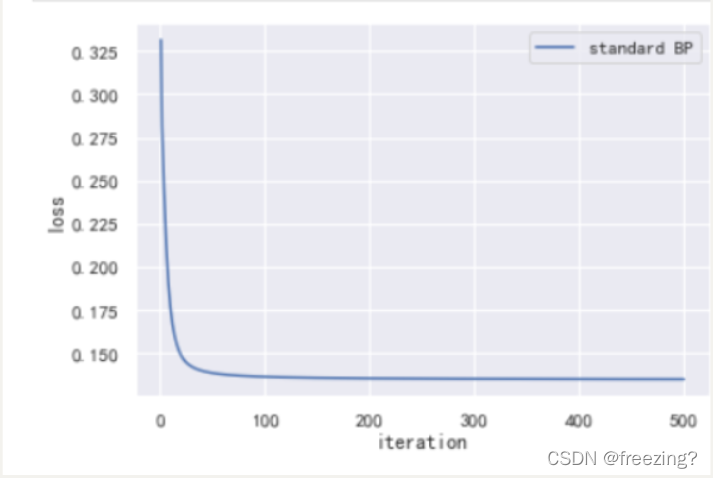
2、研究神经元个数
隐藏层为1
隐藏层为10
隐藏层为100
隐藏层为1000
分析:在学习率为0.1,迭代次数为500前提下,隐藏层需设置比较低的值,但是不宜过低,隐藏层设置太高会导致曲线紊乱。
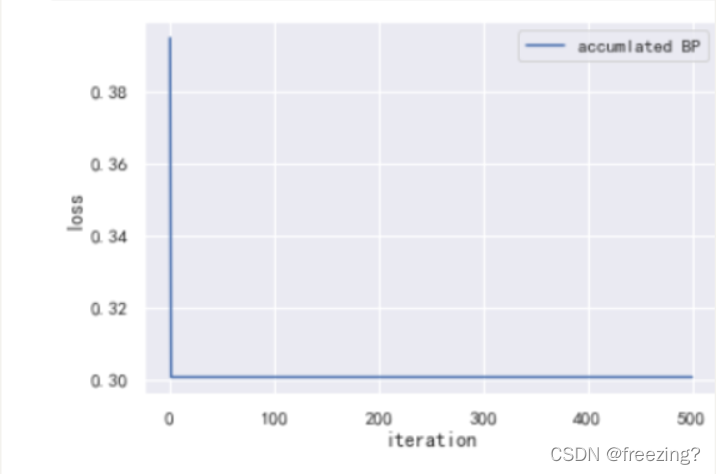
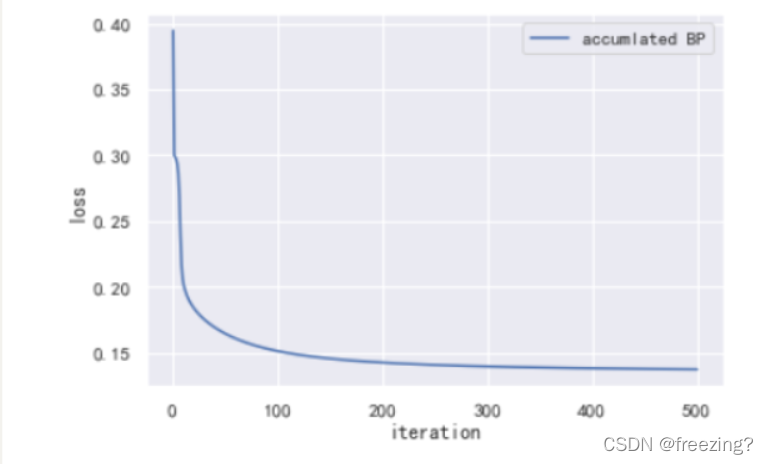
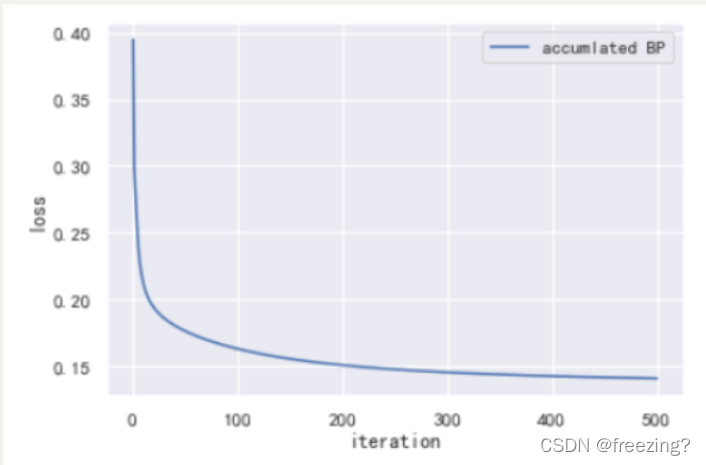
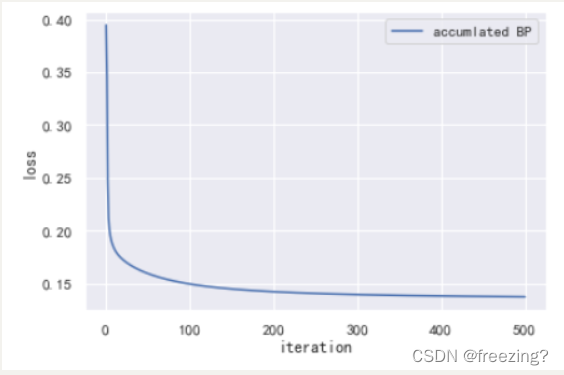
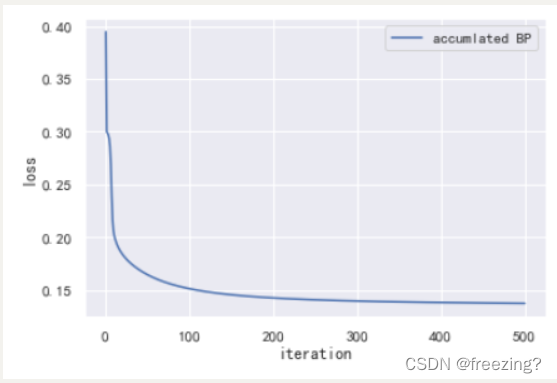
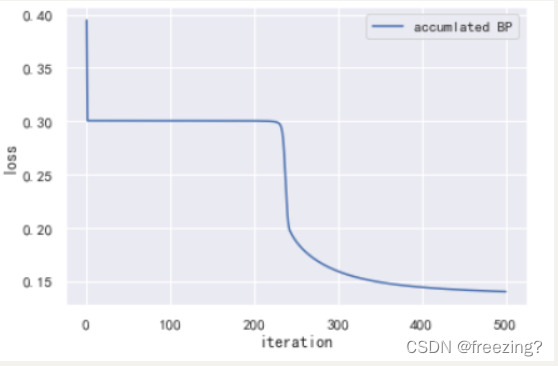
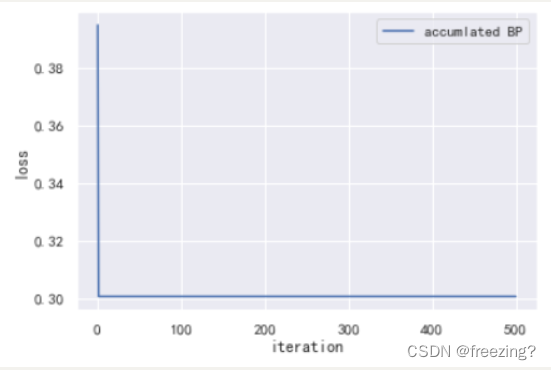
2)累计BP算法
1、研究学习率
学习率为0.5
学习率为0.1
学习率为0.05
分析:在隐藏层为10,迭代次数为500的前提下,学习率过高的情况导致曲线瞬间完成收敛结果不可靠,学习率需要低一些但是随着学习率降低收敛速度会下降,导致算法性能降低。
2、研究神经元个数
隐藏层为1
隐藏层为10
隐藏层为20
隐藏层为50
分析:在学习率为0.1,迭代次数为500前提下,隐藏层越低算法性能越高,隐藏层越高,曲线越容易紊乱,隐藏层到50以上曲线直接崩溃。
3、混淆矩阵和准确率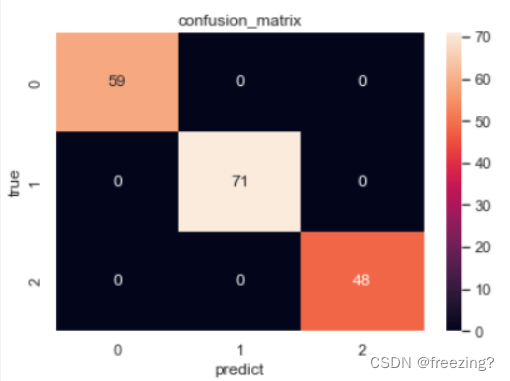
(2)TF使用
1)研究学习率
学习率为0.01
学习率为0.005
学习率为0.001
分析:由上述结果可知,在一定范围内随着学习率的增加,算法性能先提高后降低。所以为了提高算法性能我们可以选增加学习率,但首先要确定好大概范围。
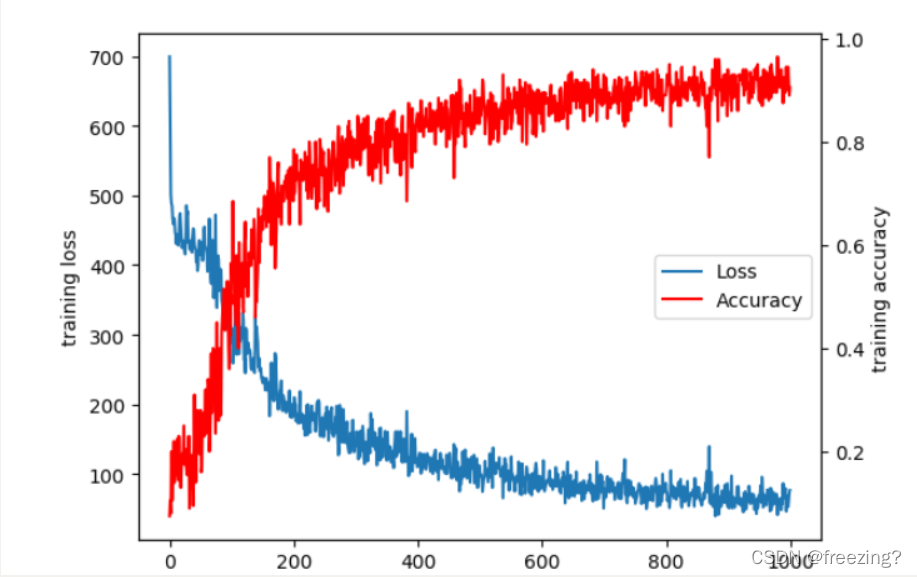
2)绘制曲线
分析:loss随着迭代次数降低收敛,准确率随着迭代次数上升收敛
3)研究神经元个数(学习率为0.005)
中间层为50
中间层为100
中间层为500
中间层为1000
分析:算法性能随着节点个数增加,先提高后降低。