获取更多资讯，赶快关注上面的公众号吧！

第一章 群体智能和进化计算

优化问题存在于科学、工程和工业的各个领域。在许多情况下，此类优化问题，特别是在当前场景中，涉及各种决策变量、复杂的结构化目标和约束。通常，经典或传统的优化技术在以其原始形式求解此类现实优化问题时都会遇到困难。由于经典优化算法在求解大规模、高度非线性、通常不可微的问题时存在不足，因此需要开发高效、鲁棒的计算算法，无论问题大小，都可以对其进行求解。从自然中获得灵感，开发计算效率高的算法是处理现实世界优化问题的一种方法。从广义上讲，我们可以将这些算法应用于计算科学领域，尤其是计算智能领域。计算智能(CI)是一组受自然启发的计算方法和途径，用于解决复杂的现实世界问题。CI主要包括模糊系统（Fuzzy Systems，FS）、神经网络（Neural Networks，NN）、群体智能（Swarm
Intelligence，SI）和进化计算（Evolutionary Computation，EC）。计算智能技术具有强大、高效、灵活、可靠等诸多优点，其中群体智能和进化计算是计算智能的两个非常有用的组成部分，主要用于解决优化问题。本部分内容主要关注各种群体和进化优化算法。

1.1 群体智能

单词“Swarm”指的是一群无序移动的个体或对象，如昆虫，鸟，鱼。更正式地讲，群体可以看作是相互作用的同类代理或个体的集合。通过建模和模拟这些个体的觅食行为，研究人员已经开发了许多有用的算法。“群体智能”一词是由Beni和Wang[1]在研究移动机器人系统时提出的。他们开发了一套控制机器人群的算法，然而，早期的研究或多或少地都利用了鸟类的群居行为。例如，1987年Reynolds[2]开发了一套程序，使用个体行为来模拟鸟类或其他动物的觅食行为。

群体智能是一门研究自然和人工系统的学科，由许多个体组成，这些个体基于社会实体间分散的、集体的和自组织的的合作行为进行协调，如鸟群、鱼群、蚁群、动物放牧、细菌生长和微生物智能。群体的成员必须是活跃的、动态的和简单的（没有或几乎没有对周围环境的固有知识）。在群体内部，由于这种协作行为，出现了一种比随机搜索更好的搜索策略，所得到的智能搜索策略一般称为群体智能。Bonabeau等人[3]对群体智能的一个广为接受的定义是，由简单的个体组成的群体所产生的集体智慧。

在80年代后期的前期工作基础上，90年代先后开发出了两种成功的算法，分别是1992年的蚁群优化算法[4]和1995年的粒子群优化算法[5]。直到90年代中期，由于种群利用、随机性和应用领域的相似性，群体智能方法一直被认为是进化计算方法。然而，由于SI和EC的基本理念存在着一些内在的差异，SI在今天有了自己的身份。SI试图模拟简单代理的集体和协同行为，而EC则受到生物进化的启发。SI作为一种优化算法，由于其简单、有效的特点，在解决实际问题中得到了广泛的应用。

Karaboga[6]给出了群体智能的充分性条件。Karaboga认为，当且仅当群体智能满足自组织和分工两个条件时，一组同类智能体才能表现出群体智能。

1.1.1 自组织

这是一个起初是无序的群体，通过群体中个体间的局部相互作用，使运动变得有序的过程。Bonabeau等人[3]将自组织分为四种策略：

• 正反馈：这是从输出系统中提取的信息，并传递给输入系统，以促进适当结构的形成。正反馈为群体智能提供多样性。

• 负反馈：用于平衡正反馈，稳定集体模式。负反馈指的是群体智能中的利用。

• 波动：这些与系统的随机性有关。波动在这一过程中提供了新的情况，有助于摆脱停滞。

• 多重交互：这提供了向社会中多个个体学习的方式，并提高了群体的整体智能。

1.1.2 分工

分工有助于不同的专业个体同时执行不同的任务，使的群体能够处理搜索空间中变化的情况。下面列出的是一些常用和成功的群智能算法：

• 粒子群优化（Particle Swarm Optimization，PSO）[5]

• 蜘蛛猴优化（Spider Monkey Optimization，SMO）[7]

• 人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[6]

• 蚁群优化（Ant Colony Optimization，ACO）[4]

• 细菌觅食优化（Bacterial Foraging Optimization，BFO）[8]

• 萤火虫算法（Firefly algorithm）[9]

粒子群优化(PSO)的灵感来源于鸟类的群集或鱼群的聚集，人工蜂群优化(ABC)的灵感来源于蜜蜂的觅食行为，蚁群优化(ACO)的灵感来源于蚂蚁的觅食行为，细菌觅食优化(BFO)的灵感来自于大肠杆菌和黄原胶等细菌的群体觅食;萤火虫算法(Firefly Algorithm, FFA)的灵感来自萤火虫的闪烁行为，而蜘蛛猴优化(Spider Monkey Optimization, SMO)的灵感来自蜘蛛猴的觅食行为。

通过文献检索发现，在这些算法中，PSO和蚁群算法是最常用的。因此，可以简要地讨论这两种算法。

粒子群优化(PSO)是受鸟群或鱼群的社会行为启发而产生的，于1995年由Kennedy和Eberhart[5]提出。通常，一群鸟没有领头，它们通过合作试错的方式来寻找食物，跟随群体中与食物源位置最接近的个体移动，其他个体则通过与已经拥有更好位置的个体沟通来同时更新他们的位置，重复这个过程，直到找到最佳的食物源。粒子群优化是由许多个体组成，这些构成一个群体，每个个体称为一个粒子，表示多维搜索空间中的一个位置或可能的候选解。

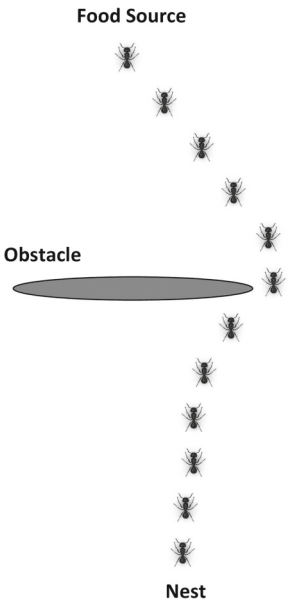
蚁群优化(ACO)[4]是群体智能第一个成功的例子，该算法用于在图中寻找最优路径。蚁群优化算法的灵感来自蚂蚁寻找巢穴与食物源之间最短路径的能力（图1）。蚂蚁初始时随机开始觅食，一旦蚂蚁找到食物源，它将按原路返回巢穴，并在路上留下信息素。这种信息素的浓度可以引导其他蚂蚁寻找食物，当其他蚂蚁发现信息素时，它们会沿着这条路径前进，其概率与信息素的浓度成正比。现在，如果其他蚂蚁也能找到食物源，它们也会在返回巢穴时留下信息素。随着越来越多的蚂蚁找到了路径，信息素的浓度也越来越高。信息素也会随着时间的推移而衰减，因此与较短的路径相比，较长的路径会有更多的衰减蒸发。蚁群算法在求解离散优化问题中得到了广泛的应用。旅行商问题、机器人路径规划、最小生成树、数据挖掘、分类、调度问题等都体现了蚁群算法在提供有效解决方案方面的优势。

进化计算

植物、动物、鸟类等生物在不断地进化，使自己适应动态的环境。与其他候选人相比，那些足够强壮(更适应环境)的候选人更有可能产生能够存活下来的后代。达尔文进化论和自然选择法则是这种进化的原因，进化计算的灵感就是来自于生物进化。很难确切地说明什么时候第一次使用进化原理来解决计算问题。然而，为了给出一些概念，在这里引用De
Jong等人[10]的描述，“有关使用进化过程解决计算机问题的最早描述之一出现在Friedberg[11]和Friedberg等人[12]的文章中。这代表了机器学习的一些早期工作，并描述了使用进化算法用于自动编程，即寻找计算给定输入输出函数的程序的任务。”想了解更多关于进化计算的历史，读者可以直接参考到De
Jong等人的成果[10]。

进化计算(EC)主要用于求解优化问题。进化计算是一系列基于生物进化原理(如自然选择和遗传)的问题解决技术的统称。这些算法试图找到全局最优解。在很短的时间内，这些技术已经在包括工程、科学和农业在内的各个领域的许多问题上得到了应用。EC在搜索过程中模拟了自然选择过程。该类算法从随机生成一组潜在解开始，然后通过迭代更新这些可能的解得到一个新的种群。更新是通过迭代应用选择、交叉和变异操作来完成的。这个过程随机丢弃不好的解，并进化出更适合(更好)的解。通过这些操作，期望所改进的解将一代一代(迭代)地变得更好。

1.2.1 进化计算成员

有很多不同的算法都属于EC，如遗传算法(GAs)[13]、遗传规划(GP)[14]、进化规划(EP)[15]和进化策略(ES)[16]。除GP外，EC的其他成员解决优化问题。另一方面，GP通常会找到能够解决给定问题的程式。遗传算法的进化基于达尔文适者生存原则，个体的编码通常是作为二进制向量来完成的，而如前所述，GP虽然使用了与遗传算法相同的适者生存原则，但进化个体是程式。进化规划的灵感来自于自然选择的进化论：另一方面，ES是一种基于适应和进化思想的搜索技术，它将个体编码作为实数向量。另一方面，差异进化与遗传在繁殖机制上是不同的。虽然DE与其他进化算法有许多相似之处，但它的显著不同之处在于，当前种群的距离和方向信息用于指导搜索过程。首先应用变异产生一个试探向量，然后在交叉算子内使用该试探向量产生一个后代，而在一般EA中，却是先应用交叉算子，再应用变异算子。此外，差分变异步长也受当前种群个体间差异的影响，而EA变异则是按照某种概率分布进行采用。

EC的一些非常显著的特征是：它们可以解决非常不结构化的问题，我们只需要有一种方法来评估解的质量(适合度)，而不需要目标函数的可微性。通常，进化算法被指计算上非常耗时，不适合解决非常大规模的问题。尽管这在一般情况下没毛病，但最近的一项突破带来了巨大的希望。最近的一项研究[17]表明，自定义进化算法可以处理涉及十亿个变量的整数线性规划问题。

1.3 讨论

这两种方法(SI和EC)背后的哲学主要植根于自然物体的生物学行为。这两种方法都受到自然现象的启发，也都是寻找最优解的搜索策略。群集智能是一种研究群居昆虫或动物在极少规则下的集体行为。进化算法是基于自然选择和遗传进化思想的自适应启发式搜索算法。

在群体智能中，群体中的个体成员是同一的，随着时间的推移，这种同一性会以移动的形式保留下来。但在进化算法中，种群成员会消亡并被后代取代。SI算法的灵感来自于鸟类、鱼类和蚂蚁等群体的觅食行为，在这些群体中，成员更新自己的位置只是为了适应环境。另一方面，进化算法是基于达尔文适者生存的原则。在这些算法中，利用交叉、变异等自然运算符产生新的子代来代替整个种群。

我们在上一节关于进化计算的讨论结束时，提到了应用EC解决了一个涉及十亿个变量的整数线性规划问题，这可能是任何优化方法处理过的最大的实际约束优化问题。在[17]中，作者提出了一种非常快速的基于种群的获取近似最优解的方法。这个成功的故事显然说明了EC可能还没有以正确的方式得到充分地探索研究，它强大到足以解决真正的大规模问题，因此有必要进行更多的研究，并且研究这样的算法是很重要的，因为随着先进技术的发展，会产生更多不同性质的数据，研究人员/实践者试图解决更复杂的高计算量的大规模问题。对于此类问题，传统的优化算法有时会变得不合适。此外，在大多数优化问题中，复杂系统都是用复杂的多维函数来建模的，有时不适合使用经典的优化技术。众所周知，经典或传统的优化技术在解决实际优化问题时存在一定的局限性，这主要是由于这些技术固有的解决机制，它们的效率也很大程度上取决于问题的维数以及凸或非凸等求解空间的结构。例如，单纯形法只能用于求解具有线性约束的线性目标函数，但是，当前场景中的大多数优化问题都涉及各种决策变量和复杂的结构化目标和约束(线性或非线性)，因此，传统的或数学的优化程序通常是不易于求解。如果我们对这些问题进行建模，使它们能够用经典方法解决，那么几乎可以肯定，我们将不得不对精确表达进行折衷，进而降低了解的质量。由于经典优化算法在求解大规模复杂优化问题时的局限性，基于群体智能和进化计算的算法已成为研究热点。这些技术非常有效且灵活，只需要简单修改就可以适应特定的问题需求。需要强调的是，这里并不是说EC是一种万能的方法，总是能优于经典方法，而应该是当情况需要时才会使用基于EC的方法，也就是说如果经典优化方法能有效解决，当然优先使用。例如，如果需要求解具有线性约束的二次优化问题或合理大小的线性规划问题，就必须使用经典方法，因为这些方法具有良好的数学性质和收敛结果。

1.4 结束语

对于一些复杂的优化问题，EC算法和SI算法是较好的选择，因为它们对目标的数学性质和约束条件(如凸性、连续性或显式定义)要求不高。这些方法使用随机方法，可以应用于更广泛的问题。但是，这种适用性伴随着代价，即全局最优的概率收敛性。此外，这些算法有时也无法在当前状态下在搜索空间的探索和利用之间取得适当的平衡。通常，指导搜索过程的参数的选择会变得很困难，结果可能在很大程度上取决于这些选择。考虑到这些限制，在群体智能和进化算法方面其实有很大的改进空间。为了使这些算法高效、准确、可靠，这些领域的改进和开发是一个持续不断的过程。

高计算能力的可用性促使人们利用EC和SI更有效地解决复杂的问题。群体算法和进化算法可以为解决这类问题提供工具。没有免费午餐定理告诉我们，没有单一的算法可以被指定为最佳算法，只要它经过足够多的问题的测试，总是会激励研究人员开发新的计算智能算法。群体算法和进化算法也被广泛地与其他机器学习方法融合。近年来，基于群体算法或进化算法的深度学习显示出其作为一种非常有前途的机器学习算法[13]的潜力。在此我们注意到，当目标函数复杂、不可微、非凸时，EC和SI具有一定的优势。然而，也存在数据挖掘问题，除了问题的复杂表示之外，涉及的数据量可能非常大(例如，在大气科学、卫生保健、天体物理学和社交媒体中)。在大数据时代，利用EC和SI来挖掘这样的数据集，可能会给研究人员带来巨大的挑战。这当然并不意味着没有改进的余地，而是表明我们需要在这些领域进行更多的研究工作。

参考文献

1. Beni, G. and J. Wang, Swarm Intelligence in Cellular Robotic Systems.
   Robots and Biological Systems: Towards a New Bionics? 1993, Berlin: Springer.

2. Reynolds, C., Flocks, Herds, and Schools: A Distributed Behavioral Model.
   ACM SIGGRAPH Computer Graphics, 1987. 21: p. 25-34.

3. Bonabeau, E., M. Dorigo, and G. Theraulaz, Swarm intelligence: from natural
   to artificial systems. 1999: Oxford University Press, Inc. 307.

4. Dorigo, M., Optimization, Learning and Natural Algorithms (in Italian).

6. Kennedy, J. and R. Eberhart. Particle swarm optimization. in Proceedings
   of ICNN’95 - International Conference on Neural Networks. 1995.

7. Karaboga, D., An Idea Based on Honey Bee Swarm for Numerical Optimization,
   Technical Report - TR06. Technical Report, Erciyes University, 2005.

8. Bansal, J.C., et al., Spider Monkey Optimization algorithm for numerical
   optimization. Memetic Computing, 2014. 6(1): p. 31-47.

9. Passino, K.M., Biomimicry of bacterial foraging for distributed optimization
   and control. Ieee Control Systems Magazine, 2002. 22(3): p. 52-67.

10. Yang, X.-S. Firefly Algorithms for Multimodal Optimization. in Stochastic
    Algorithms: Foundations and Applications. 2009. Berlin, Heidelberg: Springer
    Berlin Heidelberg.

11. De Jong, K., The Handbook of Evolutionary Computation. 1999.

12. M. Friedberg, R., A learning machine: Part I. Ibm Journal of Research and
    Development - IBMRD, 1958. 2: p. 2-13.

13. Friedberg, R.M., B. Dunham, and J.H. North, A Learning Machine: Part II.
    IBM Journal of Research and Development, 1959. 3(3): p. 282-287.

14. E. Goldberg, D., Genetic Algorithm in Search, Optimization, and Machine
    Learning. Addison-Wesley, Reading, Massachusetts, 1989. xiii.

15. Banzhaf, W., et al., Genetic Programming ∼ an Introduction: On the
    Automatic Evolution of Computer Programs and Its Applications. Morgan Kaufmann.

17. J. Fogel, L., A.J. Owens, and M.J. Walsh, Artificial Intelligence through
    Simulated Evolution. 1966.

18. Beyer, H.-G. and H.-P. Schwefel, Evolution strategies – A comprehensive
    introduction. Natural Computing, 2002. 1(1): p. 3-52.

19. Deb, K., C. Myburgh, and Acm, Breaking the Billion-Variable Barrier in
    Real-World Optimization Using a Customized Evolutionary Algorithm. Gecco’16:
    Proceedings of the 2016 Genetic and Evolutionary Computation Conference. 2016.
    653-660.