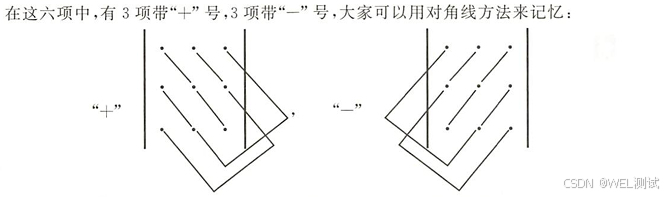
考试要求
行列式考试要求
1、了解行列式的概念,掌握行列式的性质.
2、会应用行列式的性质和行列式按行(列)展开定理计算行列式.
矩阵考试要求
1、理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.
2、掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.
3、理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.
4、了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.
5、了解分块矩阵及其运算.
行列式
行列式的概念
行列式是一个 数,它是不同行不同列元素乘积的代数和。
例如,三阶行列式子:
∣
a
1
a
2
a
3
b
1
b
2
b
3
c
1
c
2
c
3
∣
=
a
1
a
2
a
3
+
a
2
b
3
c
1
+
a
3
b
1
c
2
−
a
3
b
2
c
1
−
b
3
c
2
a
1
−
c
3
a
2
b
1
\left| \begin{matrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3 \end{matrix}\right|=a_1a_2a_3 +a_2b_3c_1+a_3b_1c_2-a_3b_2c_1-b_3c_2a_1-c_3a_2b_1
a1b1c1a2b2c2a3b3c3
=a1a2a3+a2b3c1+a3b1c2−a3b2c1−b3c2a1−c3a2b1
n阶行列式
∣
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋮
⋮
a
n
1
a
n
2
⋯
a
n
n
∣
\left| \begin{matrix} a_{11} & a_{12} &\cdots& a_{1n}\\ a_{21} & a_{22} &\cdots& a_{2n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{n1} & a_{n2} &\cdots&a_{nn} \end{matrix}\right|
a11a21⋮an1a12a22⋮an2⋯⋯⋮⋯a1na2n⋮ann
是所有取自不同行不同列的
n
n
n个元素的乘积:
a
1
j
1
a
2
j
2
⋯
a
n
j
n
a_{1j_1}a_{2j_2}\cdots a_{nj_n}
a1j1a2j2⋯anjn的代数和,这
j
1
,
j
2
,
⋯
,
j
n
j_1,j_2,\cdots ,j_n
j1,j2,⋯,jn是
1
,
2
,
⋯
,
n
1,2,\cdots,n
1,2,⋯,n的一个排列。当
j
1
,
j
2
,
⋯
,
j
n
j_1,j_2,\cdots ,j_n
j1,j2,⋯,jn是偶排列,该项的前面带+;
j
1
,
j
2
,
⋯
,
j
n
j_1,j_2,\cdots ,j_n
j1,j2,⋯,jn是奇排列,该项前面带- , 即
∣
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋮
⋮
a
n
1
a
n
2
⋯
a
n
n
∣
=
∑
j
1
,
j
2
,
⋯
,
j
n
(
−
1
)
τ
(
j
1
,
j
2
,
⋯
,
j
n
)
a
1
j
1
a
2
j
2
⋯
a
n
j
n
\left| \begin{matrix} a_{11} & a_{12} &\cdots& a_{1n}\\ a_{21} & a_{22} &\cdots& a_{2n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{n1} & a_{n2} &\cdots&a_{nn} \end{matrix}\right|=\sum_{j_1,j_2,\cdots ,j_n}(-1)^{\tau(j_1,j_2,\cdots ,j_n)}a_{1j_1}a_{2j_2}\cdots a_{nj_n}
a11a21⋮an1a12a22⋮an2⋯⋯⋮⋯a1na2n⋮ann
=j1,j2,⋯,jn∑(−1)τ(j1,j2,⋯,jn)a1j1a2j2⋯anjn
∑
j
1
,
j
2
,
⋯
,
j
n
\sum_{j_1,j_2,\cdots ,j_n}
∑j1,j2,⋯,jn表示对所有
n
n
n 阶排列求和,上式称为
n
n
n阶行列式的完全展开式。
三阶行列式的对角线法在四阶及以上不可用,计算四阶及以上必须用展开式公式法。
TIPS:
1、所谓排列是指由 n n n个数 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n所构成的一个有序数组,通常用 j 1 , j 2 , ⋯ , j n j_1,j_2,\cdots ,j_n j1,j2,⋯,jn表示 n n n阶排列,显然共有 n ! n! n!个 n n n阶排列。
2、一个排列中,如果一个大的数排在小的数之前,称这两个数构成逆序。一个排列的逆序总数称为这个排列的逆序数,用 τ ( j 1 , j 2 , ⋯ , j n ) \tau(j_1,j_2,\cdots ,j_n) τ(j1,j2,⋯,jn)表示排列 j 1 , j 2 , ⋯ , j n j_1,j_2,\cdots ,j_n j1,j2,⋯,jn的逆序数。
3、如果一个排列的逆序数是偶数,则称这个排列为偶排列,否则奇排列
例如: a 11 a 24 a 33 a 41 a_{11}a_{24}a_{33}a_{41} a11a24a33a41 是四阶行列式中的一项,那么该项所带符号由 τ ( 2431 ) \tau(2431) τ(2431)=1+2+1=4(2有1个逆序,4有两个逆序,3有一个逆序)是偶排列,取正号
a 13 a 25 a 32 a 43 a 54 a_{13}a_{25}a_{32}a_{43}a_{54} a13a25a32a43a54 是5阶行列式中的一项,那么该项所带符号由 τ ( 35124 ) \tau(35124) τ(35124)=2+3=5(3有2个逆序,5有3个逆序)是奇排列
练习1:4阶行列式
∣
A
∣
=
∣
0
0
0
a
0
0
b
0
0
c
0
0
d
0
0
0
∣
|A|=\left| \begin{matrix} 0 & 0 &0& a\\ 0 & 0 &b& 0\\ 0 &c &0& 0\\ d & 0 &0& 0 \end{matrix}\right|
∣A∣=
000d00c00b00a000
解: ∣ A ∣ = A 14 A 23 A 32 A 41 , τ ( 4321 ) = 3 + 2 + 1 = 6 故 ∣ A ∣ = a b c d |A|=A_{14}A_{23}A_{32}A_{41},\tau(4321)=3+2+1=6\\ \quad \\ 故|A|=abcd ∣A∣=A14A23A32A41,τ(4321)=3+2+1=6故∣A∣=abcd
练习2:写出4阶行列式中含有
a
12
a
34
a_{12}a_{34}
a12a34且带负号的项?
解: a 12 a 2 j 2 a 34 a 4 j 4 ⇒ j 2 j 4 只能取 13 或 31 的组合 如若: 13 , τ ( 2143 ) = 1 + 0 + 1 = 2 , 为正 如若: 31 , τ ( 2341 ) = 1 + 1 + 1 = 3 , 为负数 故: a 12 a 23 a 34 a 41 a_{12}a_{2j_2}a_{34}a_{4j_4}\Rightarrow j_2j_4只能取13或31的组合\\ \quad \\ 如若:13 ,\tau(2143)=1+0+1=2,为正\\ \quad 如若:31 ,\tau(2341)=1+1+1=3,为负数 \\ \quad \\ 故:a_{12}a_{23}a_{34}a_{41} a12a2j2a34a4j4⇒j2j4只能取13或31的组合如若:13,τ(2143)=1+0+1=2,为正如若:31,τ(2341)=1+1+1=3,为负数故:a12a23a34a41
练习3:多项式
f
(
x
)
=
∣
x
2
x
1
0
2
x
−
1
1
3
1
2
x
−
1
x
5
6
2
∣
f(x)=\left| \begin{matrix} x & 2x &1& 0\\ 2 & x-1 &1& 3\\ 1 &2 &x&-1\\ x & 5 &6& 2 \end{matrix}\right|
f(x)=
x21x2xx−12511x603−12
中,
x
3
x^3
x3的系数为?
解: 通过观察如下子排列会构成 x 3 : { a 11 a 22 a 33 a 44 = ( − 1 ) τ ( 1234 ) = 0 ( 2 x 3 − 2 x 2 ) a 12 a 24 a 33 a 41 = ( − 1 ) τ ( 2431 ) = 1 + 2 + 1 ( 6 x 3 ) 综上可知 x 3 的系数为 8 通过观察如下子排列会构成x^3:\\ \quad \\ \begin{cases}a_{11}a_{22}a_{33}a_{44}=(-1)^{\tau(1234)=0}(2x^3-2x^2) \\ \quad \\ a_{12}a_{24}a_{33}a_{41}=(-1)^{\tau(2431)=1+2+1}(6x^3)\end{cases}\\ \quad \\ 综上可知x^3的系数为8 通过观察如下子排列会构成x3:⎩ ⎨ ⎧a11a22a33a44=(−1)τ(1234)=0(2x3−2x2)a12a24a33a41=(−1)τ(2431)=1+2+1(6x3)综上可知x3的系数为8
行列式的性质
记
∣
A
∣
=
∣
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋮
⋮
a
n
1
a
n
2
⋯
a
n
n
∣
,
∣
A
T
∣
=
∣
a
11
a
21
⋯
a
n
1
a
12
a
22
⋯
a
n
2
⋮
⋮
⋮
⋮
a
1
n
a
2
n
⋯
a
n
n
∣
|A|=\left| \begin{matrix} a_{11} & a_{12} &\cdots& a_{1n}\\ a_{21} & a_{22} &\cdots& a_{2n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{n1} & a_{n2} &\cdots&a_{nn} \end{matrix}\right|,|A^{T}|=\left| \begin{matrix} a_{11} & a_{21} &\cdots& a_{n1}\\ a_{12} & a_{22} &\cdots& a_{n2}\\ \vdots & \vdots &\vdots& \vdots\\ a_{1n} & a_{2n} &\cdots&a_{nn} \end{matrix}\right|
∣A∣=
a11a21⋮an1a12a22⋮an2⋯⋯⋮⋯a1na2n⋮ann
,∣AT∣=
a11a12⋮a1na21a22⋮a2n⋯⋯⋮⋯an1an2⋮ann
,行列式
∣
A
T
∣
|A^{T}|
∣AT∣称为
∣
A
∣
|A|
∣A∣的转置行列式。
性质1 经过转置行列式的值不变,即
∣
A
T
∣
=
∣
A
∣
|A^{T}|=|A|
∣AT∣=∣A∣
性质2 两行(或列)互换位置,行列式的值变号。
性质3 某行(或列)如果有公因子
k
k
k,则可把
k
k
k提出行列式记号外,即
k
∣
A
∣
k|A|
k∣A∣。
1 、某行(或列)的元素全为0,则行列式的值为0
2、若两行(或列)的元素对应成比例,行列式的值为0
性质4 如果行列式某行(或列)是两个元素之和,则可把行列式拆成两个行列式之和。
∣
a
1
+
b
1
a
2
+
b
2
a
3
+
b
3
a
4
+
b
4
c
1
c
2
c
3
c
4
d
1
d
2
d
3
d
4
f
1
f
2
f
3
f
4
∣
=
∣
a
1
a
2
a
3
a
4
c
1
c
2
c
3
c
4
d
1
d
2
d
3
d
4
f
1
f
2
f
3
f
4
∣
+
∣
b
1
b
2
b
3
b
4
c
1
c
2
c
3
c
4
d
1
d
2
d
3
d
4
f
1
f
2
f
3
f
4
∣
\left| \begin{matrix} a_1+b_1 &a_2+b_2 &a_3+b_3 & a_4+b_4 \\ c_1 & c_2 &c_3& c_4\\ d_1 & d_2 &d_3& d_4\\ f_1 & f_2 &f_3&f_4 \end{matrix}\right|=\left| \begin{matrix} a_1&a_2 &a_3 & a_4 \\ c_1 & c_2 &c_3& c_4\\ d_1 & d_2 &d_3& d_4\\ f_1 & f_2 &f_3&f_4 \end{matrix}\right|+\left| \begin{matrix} b_1 &b_2 &b_3 & b_4 \\ c_1 & c_2 &c_3& c_4\\ d_1 & d_2 &d_3& d_4\\ f_1 & f_2 &f_3&f_4 \end{matrix}\right|
a1+b1c1d1f1a2+b2c2d2f2a3+b3c3d3f3a4+b4c4d4f4
=
a1c1d1f1a2c2d2f2a3c3d3f3a4c4d4f4
+
b1c1d1f1b2c2d2f2b3c3d3f3b4c4d4f4
性质5 如果行列式某行(或列)的
k
k
k倍加到另一行(或列),行列式的值不变。
∣
a
1
a
2
a
3
a
4
c
1
c
2
c
3
c
4
d
1
d
2
d
3
d
4
f
1
f
2
f
3
f
4
∣
=
∣
a
1
a
2
a
3
a
4
c
1
c
2
c
3
c
4
d
1
+
k
a
1
d
2
+
k
a
2
d
3
+
k
a
3
d
4
+
k
a
4
f
1
f
2
f
3
f
4
∣
\left| \begin{matrix} a_1&a_2 &a_3 & a_4 \\ c_1 & c_2 &c_3& c_4\\ d_1 & d_2 &d_3& d_4\\ f_1 & f_2 &f_3&f_4 \end{matrix}\right|=\left| \begin{matrix} a_1&a_2&a_3& a_4 \\ c_1 & c_2 &c_3& c_4\\ d_1+ka_1 & d_2+ka_2 &d_3+ka_3& d_4+ka_4\\ f_1 & f_2 &f_3&f_4 \end{matrix}\right|
a1c1d1f1a2c2d2f2a3c3d3f3a4c4d4f4
=
a1c1d1+ka1f1a2c2d2+ka2f2a3c3d3+ka3f3a4c4d4+ka4f4
练习1:证明:任意的
a
,
b
,
c
a,b,c
a,b,c恒有
∣
1
1
1
a
b
c
b
+
c
a
+
c
a
+
n
∣
\left| \begin{matrix} 1&1 &1 \\ a & b &c\\ b+c & a+c &a+n \end{matrix}\right|
1ab+c1ba+c1ca+n
证: 由行列式性质五可知: ∣ 1 1 1 a b c b + c a + c a + b ∣ = r 3 = r 2 + r 2 ∣ 1 1 1 a b c b + c + a a + c + b a + b + c ∣ = 提取 ( a + b + c ) ( b + c + a ) ∣ 1 1 1 a b c 1 1 1 ∣ = r 1 / r 3 对应成比例行列式值为 0 ( b + c + a ) 0 = 0 由行列式性质五可知:\\ \quad \\ \left| \begin{matrix} 1&1 &1 \\ a & b &c\\ b+c & a+c &a+b \end{matrix}\right|\stackrel{r3=r2+r2}=\left| \begin{matrix} 1&1 &1 \\ a & b &c\\ b+c+a & a+c+b &a+b+c \end{matrix}\right|\\ \quad \\ \stackrel{提取(a+b+c)}=(b+c+a)\left| \begin{matrix} 1&1 &1 \\ a & b &c\\ 1 & 1 &1 \end{matrix}\right|\stackrel{r1/r3对应成比例行列式值为0}=(b+c+a)0=0 由行列式性质五可知: 1ab+c1ba+c1ca+b =r3=r2+r2 1ab+c+a1ba+c+b1ca+b+c =提取(a+b+c)(b+c+a) 1a11b11c1 =r1/r3对应成比例行列式值为0(b+c+a)0=0
练习2:证明
∣
b
1
+
c
1
c
1
+
a
1
a
1
+
b
1
b
2
+
c
2
c
2
+
a
2
a
2
+
b
2
b
3
+
c
3
c
3
+
a
3
a
3
+
b
3
∣
\left| \begin{matrix} b_1+c_1&c_1+a_1 &a_1+b1 \\ b_2+c_2&c_2+a_2 &a_2+b2\\ b_3+c_3&c_3+a_3 &a_3+b3 \end{matrix}\right|
b1+c1b2+c2b3+c3c1+a1c2+a2c3+a3a1+b1a2+b2a3+b3
证: 令 ∣ A ∣ = ∣ b 1 + c 1 c 1 + a 1 a 1 + b 1 b 2 + c 2 c 2 + a 2 a 2 + b 2 b 3 + c 3 c 3 + a 3 a 3 + b 3 ∣ ⇒ ∣ A T ∣ = ∣ b 1 + c 1 b 2 + c 2 b 3 + c 3 c 1 + a 1 c 2 + a 2 c 3 + a 3 a 1 + b 1 a 2 + b 2 a 3 + b 3 ∣ 由如果行列式某行 ( 或列 ) 是两个元素之和,则可把行列式拆成两个行列式之和 ∣ A T ∣ = ∣ b 1 + c 1 b 2 + c 2 b 3 + c 3 c 1 + a 1 c 2 + a 2 c 3 + a 3 a 1 + b 1 a 2 + b 2 a 3 + b 3 ∣ = 2 ∣ b 1 b 2 b 3 c 1 c 2 c 3 a 1 a 2 a 3 ∣ 由经过转置行列式的值不变,即证 ∣ A ∣ = 2 ∣ b 1 b 2 b 3 c 1 c 2 c 3 a 1 a 2 a 3 ∣ 令|A|=\left| \begin{matrix} b_1+c_1&c_1+a_1 &a_1+b_1 \\ b_2+c_2&c_2+a_2 &a_2+b_2\\ b_3+c_3&c_3+a_3 &a_3+b_3 \end{matrix}\right|\Rightarrow|A^{T}|=\left| \begin{matrix} b_1+c_1&b_2+c_2 &b_3+c_3 \\ c_1+a_1&c_2+a_2 &c_3+a_3\\ a_1+b_1&a_2+b_2 &a_3+b_3 \end{matrix}\right|\\ \quad \\ 由如果行列式某行(或列)是两个元素之和,则可把行列式拆成两个行列式之和\\ \quad \\ |A^{T}|=\left| \begin{matrix} b_1+c_1&b_2+c_2 &b_3+c_3 \\ c_1+a_1&c_2+a_2 &c_3+a_3\\ a_1+b_1&a_2+b_2 &a_3+b_3 \end{matrix}\right|=2\left| \begin{matrix} b_1&b_2 &b_3 \\ c_1&c_2 &c_3\\ a_1&a_2 &a_3 \end{matrix}\right|\\ \quad \\ 由经过转置行列式的值不变,即证|A|=2\left| \begin{matrix} b_1&b_2 &b_3 \\ c_1&c_2 &c_3\\ a_1&a_2 &a_3 \end{matrix}\right| 令∣A∣= b1+c1b2+c2b3+c3c1+a1c2+a2c3+a3a1+b1a2+b2a3+b3 ⇒∣AT∣= b1+c1c1+a1a1+b1b2+c2c2+a2a2+b2b3+c3c3+a3a3+b3 由如果行列式某行(或列)是两个元素之和,则可把行列式拆成两个行列式之和∣AT∣= b1+c1c1+a1a1+b1b2+c2c2+a2a2+b2b3+c3c3+a3a3+b3 =2 b1c1a1b2c2a2b3c3a3 由经过转置行列式的值不变,即证∣A∣=2 b1c1a1b2c2a2b3c3a3
练习3:证明
D
=
∣
0
a
12
a
13
−
a
12
0
a
23
−
a
13
−
a
23
0
∣
=
0
D=\left| \begin{matrix} 0&a_{12} &a_{13} \\ -a_{12} &0 &a_{23}\\ -a_{13}&-a_{23} &0 \end{matrix}\right|=0
D=
0−a12−a13a120−a23a13a230
=0
方法1用完全展开式公式证: D = ( − 1 ) τ ( 123 ) = 0 a 11 a 22 a 33 + ( − 1 ) τ ( 132 ) = 1 a 11 a 23 a 32 + ( − 1 ) τ ( 213 ) = 1 a 12 a 21 a 33 + ( − 1 ) τ ( 231 ) = 2 a 12 a 23 a 31 + ( − 1 ) τ ( 321 ) = 3 a 13 a 22 a 31 + ( − 1 ) τ ( 312 ) = 2 a 13 a 21 a 32 = 0 − 0 − 0 + a 12 a 23 a 31 − 0 + a 13 a 21 a 32 = − a 12 a 23 a 13 + a 13 a 12 a 23 = 0 D=(-1)^{\tau(123)=0}a_{11}a_{22}a_{33}+(-1)^{\tau(132)=1}a_{11}a_{23}a_{32}+(-1)^{\tau(213)=1}a_{12}a_{21}a_{33}+(-1)^{\tau(231)=2}a_{12}a_{23}a_{31}+(-1)^{\tau(321)=3}a_{13}a_{22}a_{31}+(-1)^{\tau(312)=2}a_{13}a_{21}a_{32}\\ \quad \\ =0-0-0+a_{12}a_{23}a_{31}-0+a_{13}a_{21}a_{32}\\ \quad \\ =-a_{12}a_{23}a_{13}+a_{13}a_{12}a_{23}=0 D=(−1)τ(123)=0a11a22a33+(−1)τ(132)=1a11a23a32+(−1)τ(213)=1a12a21a33+(−1)τ(231)=2a12a23a31+(−1)τ(321)=3a13a22a31+(−1)τ(312)=2a13a21a32=0−0−0+a12a23a31−0+a13a21a32=−a12a23a13+a13a12a23=0
方法2用矩阵转置证: D = ∣ 0 a 12 a 13 − a 12 0 a 23 − a 13 − a 23 0 ∣ ⇒ D T = ∣ 0 − a 12 − a 13 a 12 0 − a 23 a 13 a 23 0 ∣ D T = 每行提取 − 1 ( − 1 ) 3 ∣ 0 a 12 a 13 − a 12 0 a 23 − a 13 − a 23 0 ∣ 由经过转置行列式的值不变,可得 D T = − D 可知 D = 0 D=\left| \begin{matrix} 0&a_{12} &a_{13} \\ -a_{12} &0 &a_{23}\\ -a_{13}&-a_{23} &0 \end{matrix}\right|\Rightarrow D^{T}=\left| \begin{matrix} 0&-a_{12}&-a_{13} \\ a_{12} &0 &-a_{23}\\ a_{13}&a_{23} &0 \end{matrix}\right|\\ \quad \\ D^{T}\stackrel{每行提取-1}= (-1)^3\left| \begin{matrix} 0&a_{12} &a_{13} \\ -a_{12} &0 &a_{23}\\ -a_{13}&-a_{23} &0 \end{matrix}\right|\\ \quad \\ 由经过转置行列式的值不变,可得D^{T}=-D可知D=0 D= 0−a12−a13a120−a23a13a230 ⇒DT= 0a12a13−a120a23−a13−a230 DT=每行提取−1(−1)3 0−a12−a13a120−a23a13a230 由经过转置行列式的值不变,可得DT=−D可知D=0
行列式按行(或列)展开公式
在 n n n阶行列式 D = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ D=\left| \begin{matrix} a_{11} & a_{12} &\cdots& a_{1n}\\ a_{21} & a_{22} &\cdots& a_{2n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{n1} & a_{n2} &\cdots&a_{nn} \end{matrix}\right| D= a11a21⋮an1a12a22⋮an2⋯⋯⋮⋯a1na2n⋮ann 其中划去 a i j a_{ij} aij所在的第 i i i行,第 j j j列,由剩下元素按原来的位置排法构成的一个 n − 1 n-1 n−1阶的行列式 ∣ a 11 ⋯ a 1 , j − 1 a 1 , j + 1 ⋯ a 1 n ⋮ ⋮ ⋮ ⋮ a i − 1 , 1 ⋯ a i − 1 , j − 1 a i − 1 , j + 1 ⋯ a i − 1 , n a i + 1 , 1 ⋯ a i + 1 , j − 1 a i + 1 , j + 1 ⋯ a i + 1 , n ⋮ ⋮ ⋮ ⋮ a n 1 ⋯ a n , j − 1 a n , j + 1 ⋯ a n n ∣ \left| \begin{matrix} a_{11} & \cdots &a_{1,j-1}&a_{1,j+1}&\cdots& a_{1n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{i-1,1} & \cdots &a_{i-1,j-1}&a_{i-1,j+1}&\cdots& a_{i-1,n}\\ a_{i+1,1} & \cdots &a_{i+1,j-1}&a_{i+1,j+1}&\cdots& a_{i+1,n}\\ \vdots & \vdots &\vdots& \vdots\\ a_{n1} & \cdots & a_{n,j-1} &a_{n,j+1}&\cdots&a_{nn} \end{matrix}\right| a11⋮ai−1,1ai+1,1⋮an1⋯⋮⋯⋯⋮⋯a1,j−1⋮ai−1,j−1ai+1,j−1⋮an,j−1a1,j+1⋮ai−1,j+1ai+1,j+1⋮an,j+1⋯⋯⋯⋯a1nai−1,nai+1,nann 称其为 a i j a_{ij} aij 的余子式,记为 M i j M_{ij} Mij;称 ( − 1 ) i + j M i j (-1)^{i+j}M_{ij} (−1)i+jMij为 a i j a_{ij} aij的代数余子式,记为 A i j A_{ij} Aij即 A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
定理 1.1
n
n
n阶行列式等于它的任何一行 (列)元素与其对应的代数余子式乘积之和,即
按第
i
行展开:
∣
A
∣
=
a
i
1
A
i
1
+
a
i
2
A
i
2
+
⋯
+
a
i
n
A
i
n
=
∑
k
=
1
n
a
i
k
A
i
k
,
i
=
1
,
2
,
⋯
,
n
按第
j
列展开:
∣
A
∣
=
a
1
j
A
1
j
+
a
2
j
A
2
j
+
⋯
+
a
n
j
A
n
j
=
∑
k
=
1
n
a
k
j
A
k
j
,
j
=
1
,
2
,
⋯
,
n
按第i行展开:|A|=a_{i1}A_{i1}+a_{i2}A_{i2}+\cdots+a_{in}A_{in}=\sum_{k=1}^{n}a_{ik}A_{ik},i=1,2,\cdots,n\\ \quad \\ 按第j列展开:|A|=a_{1j}A_{1j}+a_{2j}A_{2j}+\cdots+a_{nj}A_{nj}=\sum_{k=1}^{n}a_{kj}A_{kj},j=1,2,\cdots,n
按第i行展开:∣A∣=ai1Ai1+ai2Ai2+⋯+ainAin=k=1∑naikAik,i=1,2,⋯,n按第j列展开:∣A∣=a1jA1j+a2jA2j+⋯+anjAnj=k=1∑nakjAkj,j=1,2,⋯,n
定理 1.2 行列式的任一行 (列)元素与另一行 (列)元素的代数余子式乘积之和为0
行:
∑
k
=
1
n
a
i
k
A
j
k
=
a
i
1
A
j
1
+
a
i
2
A
j
2
+
⋯
+
a
i
n
A
j
n
=
0
,
i
≠
j
行:
∑
k
=
1
n
a
k
i
A
k
j
=
a
1
i
A
1
j
+
a
2
i
A
2
j
+
⋯
+
a
n
i
A
n
j
=
0
,
i
≠
j
行:\sum_{k=1}^{n}a_{ik}A_{jk}=a_{i1}A_{j1}+a_{i2}A_{j2}+\cdots+a_{in}A_{jn}=0,i\ne j \\ \quad \\ 行:\sum_{k=1}^{n}a_{ki}A_{kj}=a_{1i}A_{1j}+a_{2i}A_{2j}+\cdots+a_{ni}A_{nj}=0,i\ne j
行:k=1∑naikAjk=ai1Aj1+ai2Aj2+⋯+ainAjn=0,i=j行:k=1∑nakiAkj=a1iA1j+a2iA2j+⋯+aniAnj=0,i=j
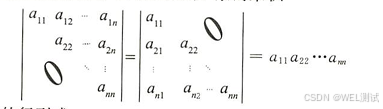
1、上(下)三角形行列式的值等于主对角线元素的乘积
2、关于负对角线的行列式等于负对角线之积乘以
(
−
1
)
n
(
n
−
1
)
2
(-1)^{\frac{n(n-1)}{2}}
(−1)2n(n−1)
3、 拉普拉斯展开式:如果
A
A
A 和
B
B
B分别是
m
m
m和
n
n
n阶矩阵,则
∣
A
∗
O
B
∣
=
∣
A
O
∗
B
∣
=
∣
A
∣
⋅
∣
B
∣
∣
A
∗
O
B
∣
=
∣
O
A
B
∗
∣
=
(
−
1
)
m
n
∣
A
∣
⋅
∣
B
∣
\left| \begin{matrix} A & *\\ O & B \end{matrix}\right|=\left| \begin{matrix} A & O\\* & B \end{matrix}\right|=|A|\cdot|B| \\ \quad \\ \left| \begin{matrix} A & *\\ O & B \end{matrix}\right|=\left| \begin{matrix} O & A\\B & * \end{matrix}\right|=(-1)^{mn}|A|\cdot|B|
AO∗B
=
A∗OB
=∣A∣⋅∣B∣
AO∗B
=
OBA∗
=(−1)mn∣A∣⋅∣B∣
4、范德蒙行列式
∣
1
1
⋯
1
x
1
x
2
⋯
x
n
x
1
2
x
2
2
⋯
x
n
2
⋮
⋮
⋮
⋮
x
1
n
−
1
x
2
n
−
1
⋯
x
n
n
−
1
∣
=
∏
1
≤
j
<
i
≤
n
(
x
i
−
x
j
)
\left| \begin{matrix} 1&1&\cdots & 1\\ x_1&x_2&\cdots & x_n\\ x_1^2&x_2^2&\cdots & x_n^2\\ \vdots&\vdots&\vdots & \vdots\\ x_1^{n-1}&x_2^{n-1}&\cdots & x_n^{n-1} \end{matrix}\right|=\prod_{1\le j <i \le n}(x_i-x_j)
1x1x12⋮x1n−11x2x22⋮x2n−1⋯⋯⋯⋮⋯1xnxn2⋮xnn−1
=1≤j<i≤n∏(xi−xj)
练习1:计算行列式的值
∣
1
4
−
1
4
2
2
2
3
3
−
1
6
2
4
0
5
3
∣
\left| \begin{matrix} 1&4&-1 & 4\\ 2&2&2 & 3\\ 3&-1&6 & 2\\ 4&0&5 & 3 \end{matrix}\right|
123442−10−12654323
解∣ 1 4 − 1 4 2 2 2 3 3 − 1 6 2 4 0 5 3 ∣ ⟹ 第一行 = 第一行 − 2 × 第二行 ∣ − 3 0 − 5 − 2 2 2 2 3 3 − 1 6 2 4 0 5 3 ∣ ⟹ 第二行 = 第二行 + 2 × 第三行 ∣ − 3 0 − 5 − 2 8 0 14 7 3 − 1 6 2 4 0 5 3 ∣ ⟹ 按第二列展开计算 ( − 1 ) ( − 1 ) 2 + 3 ∣ − 3 − 5 − 2 8 14 7 4 5 3 ∣ ⟹ 行 1 = 行 1 + 行 3 ∣ 1 0 1 8 14 7 4 5 3 ∣ ⟹ 列 1 = 列 1 − 列 3 ∣ 0 0 1 1 14 7 1 5 3 ∣ ⟹ 按第一行展开计算 ( 1 ) ( − 1 ) 1 + 3 ∣ 1 14 1 5 ∣ = 5 − 14 = − 9 \left| \begin{matrix} 1&4&-1 & 4\\ 2&2&2 & 3\\ 3&-1&6 & 2\\ 4&0&5 & 3 \end{matrix}\right|\stackrel{第一行=第一行-2\times第二行}\Longrightarrow \left| \begin{matrix} -3&0&-5 & -2\\ 2&2&2 & 3\\ 3&-1&6 & 2\\ 4&0&5 & 3 \end{matrix}\right|\\ \quad \\ \stackrel{第二行=第二行+2\times第三行}\Longrightarrow \left| \begin{matrix} -3&0&-5 & -2\\ 8&0&14 & 7\\ 3&-1&6 & 2\\ 4&0&5 & 3 \end{matrix}\right|\\ \quad \\ \stackrel{按第二列展开计算}\Longrightarrow (-1)(-1)^{2+3}\left| \begin{matrix} -3&-5 & -2\\ 8&14 & 7\\ 4&5 & 3 \end{matrix}\right| \stackrel{行1=行1+行3}\Longrightarrow \left| \begin{matrix} 1&0 & 1\\ 8&14 & 7\\ 4&5 & 3 \end{matrix}\right| \\ \quad \\ \stackrel{列1=列1-列3}\Longrightarrow \left| \begin{matrix} 0&0 & 1\\ 1&14 & 7\\ 1&5 & 3 \end{matrix}\right|\stackrel{按第一行展开计算}\Longrightarrow (1)(-1)^{1+3}\left| \begin{matrix} 1&14\\ 1&5 \end{matrix}\right|=5-14=-9 123442−10−12654323 ⟹第一行=第一行−2×第二行 −323402−10−5265−2323 ⟹第二行=第二行+2×第三行 −383400−10−51465−2723 ⟹按第二列展开计算(−1)(−1)2+3 −384−5145−273 ⟹行1=行1+行3 1840145173 ⟹列1=列1−列3 0110145173 ⟹按第一行展开计算(1)(−1)1+3 11145 =5−14=−9
练习2:计算行列式的值
∣
0
5
2
0
8
3
5
4
7
2
4
1
0
4
1
0
∣
\left| \begin{matrix} 0&5&2 & 0\\ 8&3&5 & 4\\ 7&2&4 &1\\ 0&4&1 & 0 \end{matrix}\right|
0870532425410410
解: ∣ 0 5 2 0 8 3 5 4 7 2 4 1 0 4 1 0 ∣ ⟹ 按第一行展开计算 = 5 × ( − 1 ) 3 ∣ 8 5 4 7 4 1 0 1 0 ∣ + 2 × ( − 1 ) 4 ∣ 8 3 4 7 2 1 0 4 0 ∣ = − 5 × 1 ( − 1 ) 5 ∣ 8 4 7 1 ∣ + 2 × 4 ( − 1 ) 5 ∣ 8 4 7 1 ∣ = 5 ( 8 − 28 ) − 8 ( 8 − 28 ) = 60 \left| \begin{matrix} 0&5&2 & 0\\ 8&3&5 & 4\\ 7&2&4 &1\\ 0&4&1 & 0 \end{matrix}\right|\stackrel{按第一行展开计算}\Longrightarrow=5\times(-1)^3\left| \begin{matrix} 8&5 & 4\\ 7&4 &1\\ 0&1 & 0 \end{matrix}\right|+2\times(-1)^4\left| \begin{matrix} 8&3 & 4\\ 7&2 &1\\ 0&4 & 0 \end{matrix}\right|\\ \quad \\ =-5\times 1 (-1)^5\left| \begin{matrix} 8 & 4\\ 7&1\\ \end{matrix}\right|+2\times 4 (-1)^5\left| \begin{matrix} 8& 4\\ 7 &1\\ \end{matrix}\right|=5(8-28)-8(8-28)=60 0870532425410410 ⟹按第一行展开计算=5×(−1)3 870541410 +2×(−1)4 870324410 =−5×1(−1)5 8741 +2×4(−1)5 8741 =5(8−28)−8(8−28)=60
练习3:计算行列式的值
∣
a
+
x
a
a
a
a
a
+
x
a
a
a
a
a
+
x
a
a
a
a
a
+
x
∣
\left| \begin{matrix} a+x&a&a &a\\ a&a+x&a & a\\ a&a&a+x &a\\ a&a&a & a+x \end{matrix}\right|
a+xaaaaa+xaaaaa+xaaaaa+x
解: ∣ a + x a a a a a + x a a a a a + x a a a a a + x ∣ ⟹ r 1 = r 1 + r 2 + r 3 + r 4 ( x + 4 a ) ∣ 1 1 1 1 a a + x a a a a a + x a a a a a + x ∣ ⟹ c 4 = c 4 − c 1 ( x + 4 a ) ∣ 1 1 1 0 a a + x a 0 a a a + x 0 a a a x ∣ ⟹ 按第 4 列展开 ( x + 4 a ) . x . ( − 1 ) 8 ∣ 1 1 1 a a + x a a a a + x ∣ ⟹ c 3 = c 3 − c 1 ( x + 4 a ) . x ∣ 1 1 0 a a + x 0 a a x ∣ ⟹ 按第 3 列展开 ( x + 4 a ) . x . x . ( − 1 ) 6 ∣ 1 1 a a + x ∣ = ( x + 4 a ) . x 2 ( a + x − a ) = x 3 ( x + 4 a ) \left| \begin{matrix} a+x&a&a &a\\ a&a+x&a & a\\ a&a&a+x &a\\ a&a&a & a+x \end{matrix}\right|\stackrel{r1=r1+r2+r3+r4}\Longrightarrow(x+4a)\left| \begin{matrix} 1&1&1 &1\\ a&a+x&a & a\\ a&a&a+x &a\\ a&a&a & a+x \end{matrix}\right| \\ \quad \\ \stackrel{c4=c4-c1}\Longrightarrow(x+4a)\left| \begin{matrix} 1&1&1 &0\\ a&a+x&a & 0\\ a&a&a+x &0\\ a&a&a & x \end{matrix}\right|\stackrel{ 按第4列展开}\Longrightarrow(x+4a).x.(-1)^8\left| \begin{matrix} 1&1&1 \\ a&a+x&a\\ a&a&a+x \\ \end{matrix}\right|\\ \quad \\ \stackrel{ c3=c3-c1}\Longrightarrow(x+4a).x\left| \begin{matrix} 1&1&0 \\ a&a+x&0\\ a&a&x \\ \end{matrix}\right|\stackrel{ 按第3列展开}\Longrightarrow(x+4a).x.x.(-1)^6\left| \begin{matrix} 1&1 \\ a&a+x\\ \end{matrix}\right|\\ \quad \\ =(x+4a).x^2(a+x-a)=x^3(x+4a) a+xaaaaa+xaaaaa+xaaaaa+x ⟹r1=r1+r2+r3+r4(x+4a) 1aaa1a+xaa1aa+xa1aaa+x ⟹c4=c4−c1(x+4a) 1aaa1a+xaa1aa+xa000x ⟹按第4列展开(x+4a).x.(−1)8 1aa1a+xa1aa+x ⟹c3=c3−c1(x+4a).x 1aa1a+xa00x ⟹按第3列展开(x+4a).x.x.(−1)6 1a1a+x =(x+4a).x2(a+x−a)=x3(x+4a)
练习4:计算行列式的值
∣
1
+
x
1
1
1
1
1
−
x
1
1
1
1
1
−
y
1
1
1
1
1
−
y
∣
\left| \begin{matrix} 1+x&1&1 &1\\ 1&1-x&1 & 1\\ 1&1&1-y &1\\ 1&1&1 & 1-y \end{matrix}\right|
1+x11111−x11111−y11111−y
解: ∣ 1 + x 1 1 1 1 1 − x 1 1 1 1 1 + y 1 1 1 1 1 − y ∣ ⟹ c 1 = c 1 − c 2 ∣ x 1 1 1 x 1 − x 1 1 0 1 1 + y 1 0 1 1 1 − y ∣ ⟹ 按 r 2 = r 2 − r 1 展开 ∣ x 1 1 1 0 − x 0 0 0 1 1 + y 1 0 1 1 1 − y ∣ = x . ( − 1 ) 2 ∣ − x 0 0 1 1 + y 1 1 1 1 − y ∣ ⟹ 一行展开 − x 2 . ( − 1 ) 2 ∣ 1 + y 1 1 1 − y ∣ = x 2 y 2 \left| \begin{matrix} 1+x&1&1 &1\\ 1&1-x&1 & 1\\ 1&1&1+y &1\\ 1&1&1 & 1-y \end{matrix}\right|\stackrel{ c1=c1-c2}\Longrightarrow\left| \begin{matrix} x&1&1 &1\\ x&1-x&1 & 1\\ 0&1&1+y &1\\ 0&1&1 & 1-y \end{matrix}\right|\\ \quad \\ \stackrel{按r2=r2-r1展开}\Longrightarrow\left| \begin{matrix} x&1&1 &1\\ 0&-x&0& 0\\ 0&1&1+y &1\\ 0&1&1 & 1-y \end{matrix}\right|=x.(-1)^2\left| \begin{matrix} -x&0& 0\\ 1&1+y &1\\ 1&1 & 1-y \end{matrix}\right|\\ \quad \\ \stackrel{一行展开}\Longrightarrow -x^2.(-1)^2\left| \begin{matrix} 1+y &1\\ 1 & 1-y \end{matrix}\right|=x^2y^2 \quad \quad \quad \quad \quad \quad \quad \quad \quad 1+x11111−x11111+y11111−y ⟹c1=c1−c2 xx0011−x11111+y11111−y ⟹按r2=r2−r1展开 x0001−x11101+y11011−y =x.(−1)2 −x1101+y1011−y ⟹一行展开−x2.(−1)2 1+y111−y =x2y2
练习5:已知
∣
λ
−
1
1
−
1
−
2
λ
−
4
2
3
3
λ
−
5
∣
=
0
\left| \begin{matrix} \lambda-1&1&-1\\ -2&\lambda-4&2 \\ 3&3&\lambda-5 \end{matrix}\right|=0
λ−1−231λ−43−12λ−5
=0,求
λ
\lambda
λ
解: ∣ λ − 1 1 − 1 − 2 λ − 4 2 3 3 λ − 5 ∣ ⟹ c 3 = c 3 − c 2 ∣ λ − 1 1 0 − 2 λ − 4 λ − 2 3 3 λ − 2 ∣ ⟹ r 2 = r 2 − r 3 ∣ λ − 1 1 0 − 5 λ − 7 0 3 3 λ − 2 ∣ ⟹ 按 c 3 展开 ( λ − 2 ) ( − 1 ) 6 ∣ λ − 1 1 − 5 λ − 7 ∣ = ( λ − 2 ) 2 ( ( λ − 6 ) ) λ 1 = λ 2 = 2 , λ 3 = 6 \left| \begin{matrix} \lambda-1&1&-1\\ -2&\lambda-4&2 \\ 3&3&\lambda-5 \end{matrix}\right|\stackrel{c3=c3-c2}\Longrightarrow \left| \begin{matrix} \lambda-1&1&0\\ -2&\lambda-4&\lambda-2 \\ 3&3&\lambda-2 \end{matrix}\right|\\ \quad \\ \stackrel{r2=r2-r3}\Longrightarrow \left| \begin{matrix} \lambda-1&1&0\\ -5&\lambda-7&0 \\ 3&3&\lambda-2 \end{matrix}\right|\stackrel{ 按c3展开}\Longrightarrow(\lambda-2)(-1)^6\left| \begin{matrix} \lambda-1&1\\ -5&\lambda-7\\ \end{matrix}\right|=(\lambda-2)^2((\lambda-6))\\ \quad \\ \lambda_1=\lambda_2=2,\lambda_3=6 λ−1−231λ−43−12λ−5 ⟹c3=c3−c2 λ−1−231λ−430λ−2λ−2 ⟹r2=r2−r3 λ−1−531λ−7300λ−2 ⟹按c3展开(λ−2)(−1)6 λ−1−51λ−7 =(λ−2)2((λ−6))λ1=λ2=2,λ3=6
克拉默法则
若
n
n
n个方程
n
n
n个未知量构成的非齐次线性方程组
{
a
11
x
1
+
a
12
x
2
+
⋯
+
a
1
n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+
⋯
+
a
2
n
x
n
=
b
2
⋯
⋯
⋯
⋯
a
n
1
x
1
+
a
n
2
x
2
+
⋯
+
a
n
n
x
n
=
b
n
\begin{cases}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \\ \quad \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2 \\ \quad \\ \cdots \cdots \cdots \cdots \\ \quad \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{cases}
⎩
⎨
⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯an1x1+an2x2+⋯+annxn=bn的系数行列式
∣
A
∣
≠
0
|A|\ne0
∣A∣=0,则上式有唯一解,且
x
i
=
∣
A
i
∣
∣
A
∣
,
i
=
1
,
2
,
⋯
,
n
x_i=\frac{|A_i|}{|A|},\quad i=1,2,\cdots,n
xi=∣A∣∣Ai∣,i=1,2,⋯,n其中
∣
A
i
∣
|A_i|
∣Ai∣是
∣
A
∣
|A|
∣A∣中第
i
i
i列元素(即
x
i
x_i
xi的系数)替换成方程组右端的常数项
b
1
,
b
2
,
⋯
,
b
n
b_1,b_2,\cdots,b_n
b1,b2,⋯,bn所构成的行列式。
注:若
∣
A
∣
=
0
|A|=0
∣A∣=0,方程组可能无解,也可能有无穷多解,但一定不是有唯一解。
推论 若包含
n
n
n个方程
n
n
n个未知量的齐次线性方程组
{
a
11
x
1
+
a
12
x
2
+
⋯
+
a
1
n
x
n
=
0
a
21
x
1
+
a
22
x
2
+
⋯
+
a
2
n
x
n
=
0
⋯
⋯
⋯
⋯
a
n
1
x
1
+
a
n
2
x
2
+
⋯
+
a
n
n
x
n
=
0
\begin{cases}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=0 \\ \quad \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=0 \\ \quad \\ \cdots \cdots \cdots \cdots \\ \quad \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=0 \end{cases}
⎩
⎨
⎧a11x1+a12x2+⋯+a1nxn=0a21x1+a22x2+⋯+a2nxn=0⋯⋯⋯⋯an1x1+an2x2+⋯+annxn=0
的系数行列式
∣
A
∣
≠
0
|A|\ne0
∣A∣=0,则上式只有零解。 若齐次线性方程组有非零解,则其系数行列式必为0,即
∣
A
∣
=
0
|A|=0
∣A∣=0
练习1:方程组
{
x
1
+
x
2
+
x
3
=
1
2
x
1
−
x
2
−
3
x
3
=
0
4
x
1
+
x
2
+
9
x
3
=
0
\begin{cases}x_1+x_2+x_3=1 \\ \quad \\ 2x_1-x_2-3x_3=0 \\ \quad \\ 4x_1+x_2+9x_3=0\end{cases}
⎩
⎨
⎧x1+x2+x3=12x1−x2−3x3=04x1+x2+9x3=0
的解中,
x
1
=
x_1=
x1=?
解: 令上述方程系数行列式为 D = ∣ 1 1 1 2 − 1 − 3 4 1 9 ∣ 观察 D 为范德蒙德行列式: D = ∏ 1 ≤ j < i ≤ 3 ( x i − x j ) = ( − 1 − 2 ) ( − 3 − 2 ) ( − 3 + 1 ) = − 30 D 1 = ∣ 1 1 1 0 − 1 − 3 0 1 9 ∣ = 1. ( − 1 ) 2 ∣ − 1 − 3 1 9 ∣ = − 6 x 1 = D 1 D = − 6 − 30 = 1 5 令上述方程系数行列式为D=\left|\begin{matrix} 1&1&1\\ 2&-1&-3\\ 4&1&9\\ \end{matrix}\right| \\ \quad \\ 观察D为范德蒙德行列式:D=\prod_{1\le j <i \le 3}(x_i-x_j)=(-1-2)(-3-2)(-3+1)=-30\\ \quad \\ D_1=\left|\begin{matrix} 1&1&1\\ 0&-1&-3\\ 0&1&9\\ \end{matrix}\right|=1.(-1)^2\left|\begin{matrix} -1&-3\\ 1&9\\ \end{matrix}\right|=-6\\ \quad \\x_1=\frac{D_1}{D}=\frac{-6}{-30}=\frac{1}{5} 令上述方程系数行列式为D= 1241−111−39 观察D为范德蒙德行列式:D=1≤j<i≤3∏(xi−xj)=(−1−2)(−3−2)(−3+1)=−30D1= 1001−111−39 =1.(−1)2 −11−39 =−6x1=DD1=−30−6=51