文章目录
1. seq2seq模型介绍
传统的RNN只能处理 1 to N,N to N,N to 1 的问题,即输入长度为1输出长度为N,输入长度为N输出长度为N,输入长度为N输出长度为1的问题,但是,对于像翻译这种问题,输入与输出的序列并没有明确的一对一或一对多的关系的,可以称之为 N to M 问题,即输入与输出的长度都不固定,传统的模型就不能够解决这个问题,于是,RNN的变种seq2seq模型就被提出来了。
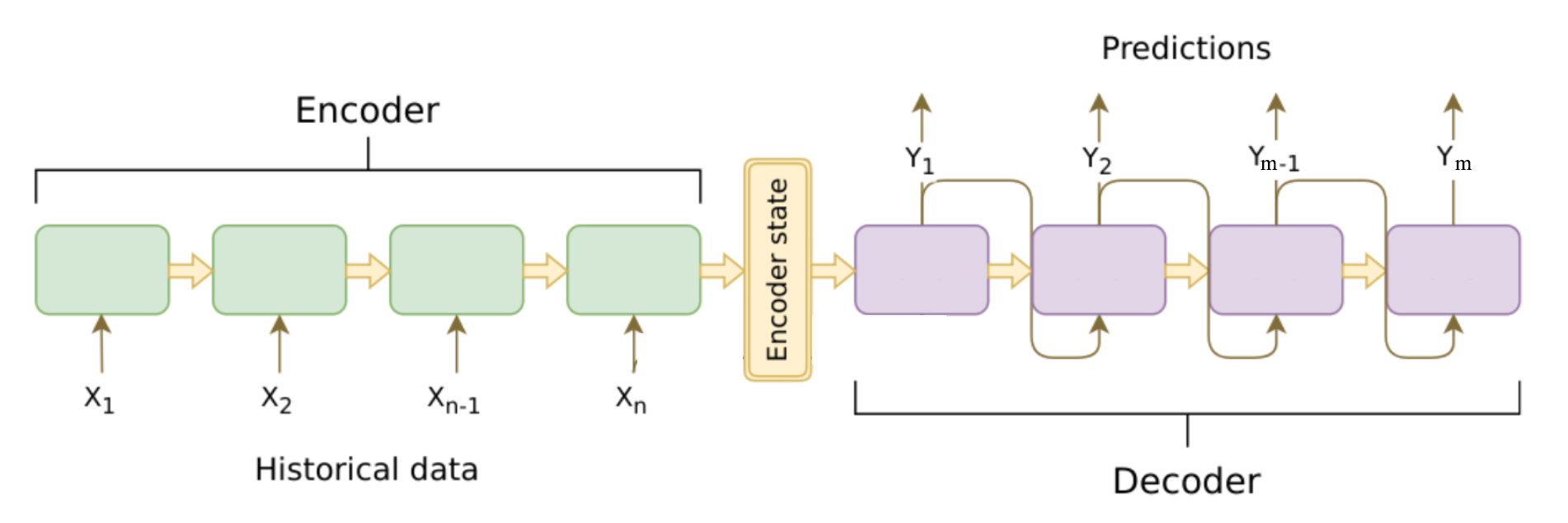
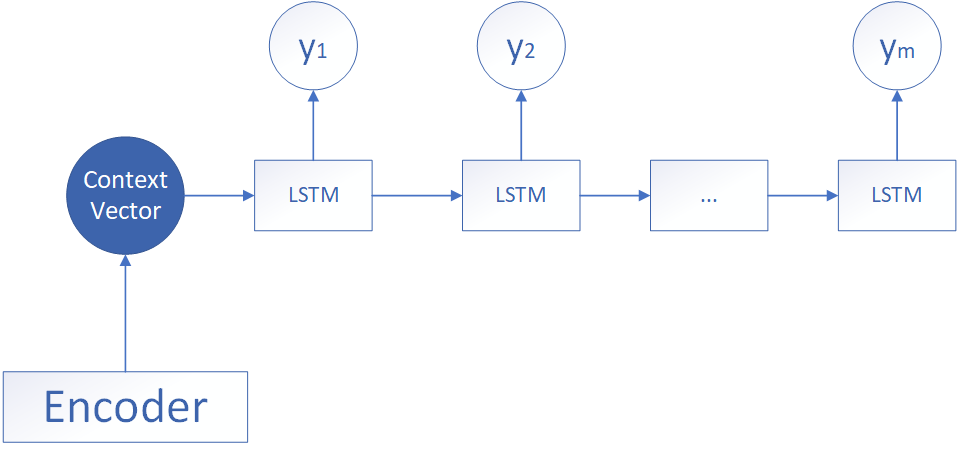
seq2seq模型是一种RNN模型的变体,其结构如下,模型组成包含了Encoder–Decoder 的结构,Encoder和Decoder都是一个RNN结构,Encoder是编码器,接受一个输入序列,输入序列长度为 N ,并将其输出成一个中间语义向量,Decoder是解码器,其接收Encoder产生的中间语义向量,并输出一个长度为 M 的序列。当需要计算损失的时候,将输出的序列与目标值计算相应的损失即可。
以上就是seq2seq模型的大致计算流程,接下来我们对其流程进行详细的介绍。
2. 模型计算
上述过程中的Encoder以及Decoder都使用的是RNN,现在使用的时候一般都使用的是RNN的变体LSTM,LSTM比原始的RNN结构更加的巧妙,更有希望能够记住长句子,首先我们先来认识一下LSTM的结构。
2.1 LSTM结构单元
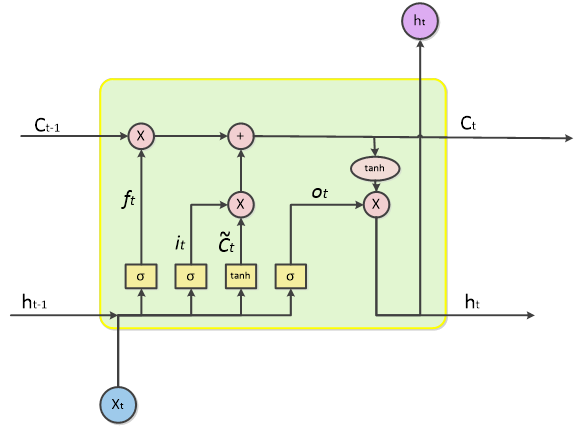
一个LSTM单元的结构如下所示:
上述结构中,我们称
h
t
h_t
ht 为
t
t
t 时刻的隐藏状态,
C
t
C_t
Ct 为
t
t
t 时刻的输出状态,LSTM的结构单元接收一个序列
X
t
X_t
Xt 的输入和上一个时刻的隐藏状态
h
t
−
1
h_{t-1}
ht−1 以及输出状态
C
t
−
1
C_{t-1}
Ct−1 ,经过其中结构的一系列运算,得到当前时刻的隐藏状态
h
t
h_t
ht 以及输出状态
C
t
C_t
Ct ,进行的一系列运算并不重要,深度学习框架中的包会自动帮我们进行计算的,重要的是这里的
h
t
,
C
t
h_t,C_t
ht,Ct 。
2.2 seq2seq计算流程
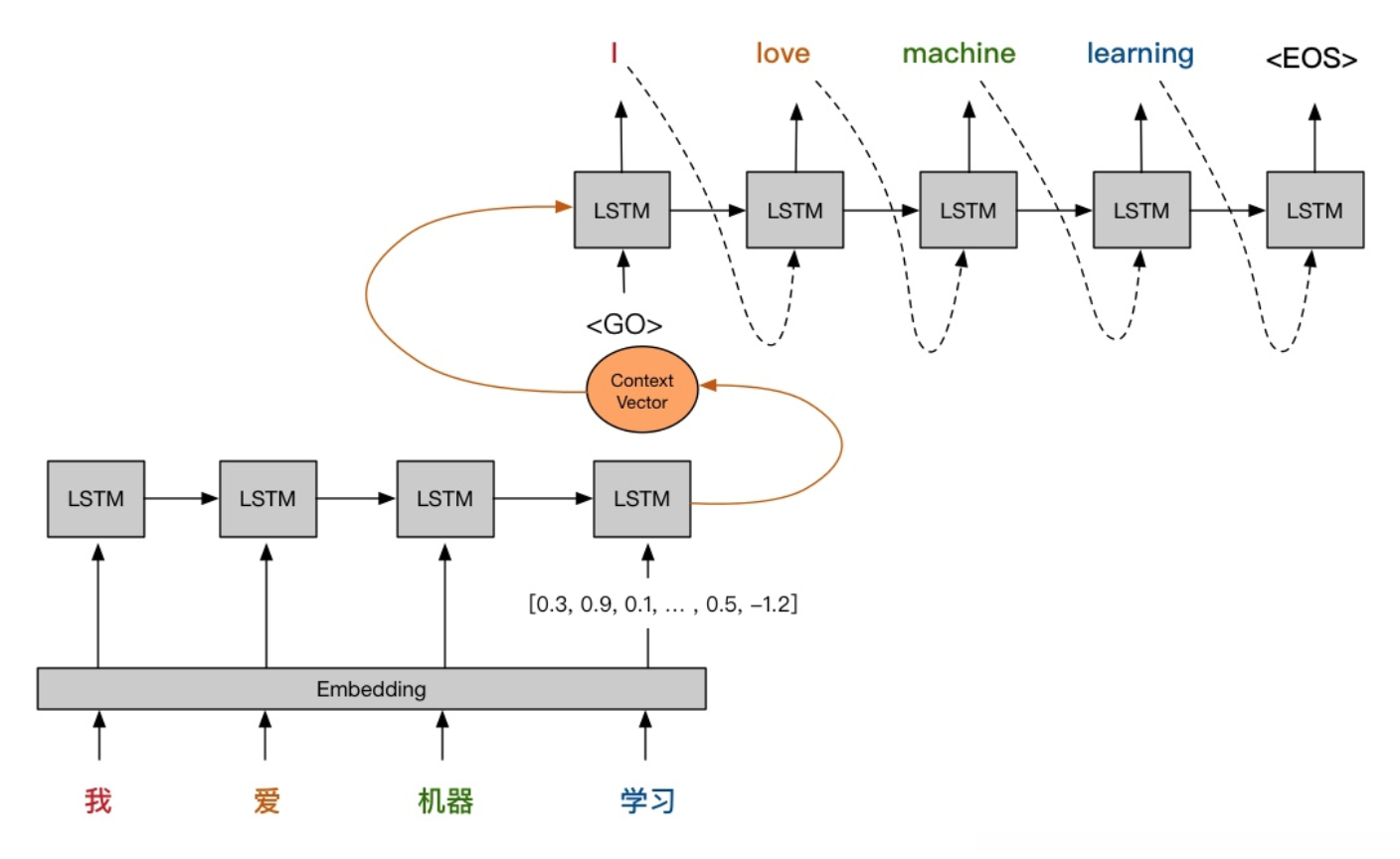
比如我们现在有一个机器翻译的任务,使用的是seq2seq模型,模型的结构如下:
设输入序列为
x
=
(
x
1
,
x
2
,
⋯
,
x
n
)
x=(x_1,x_2,\cdots,x_n)
x=(x1,x2,⋯,xn),输出序列为
y
=
(
y
1
,
y
2
,
⋯
,
y
m
)
y=(y_1,y_2,\cdots,y_m)
y=(y1,y2,⋯,ym),首先,将输入序列通过LSTM,得到最后一个状态的隐藏状态和输出状态,即
h
n
,
c
n
=
L
S
T
M
(
x
,
h
n
−
1
,
c
n
−
1
)
h_n,c_n=LSTM(x,h_{n-1},c_{n-1})
hn,cn=LSTM(x,hn−1,cn−1)一般而言,这里的
C
o
n
t
e
x
t
V
e
c
t
o
r
Context \hspace{0.5em} Vector
ContextVector 传递的是最后一个状态的
h
n
h_n
hn 和
c
n
c_n
cn ,即
C
=
[
h
n
,
c
n
]
C=[h_n,c_n]
C=[hn,cn] 。
然后,将上下文向量
C
C
C 传入解码器中,并将其逐步传入到每一个时间步的LSTM,每一个时间步使用softmax层输出一个概率最大的序列
y
^
i
\hat{y}_i
y^i,将输出的序列
y
^
\hat{y}
y^ 与
y
y
y 使用损失函数计算损失,再进行反向传播逐步训练即得到了seq2seq模型。
3. Attention机制
在Seq2Seq结构中,encoder把所有的输入序列都编码成一个统一的语义向量context,然后再由Decoder解码。由于context包含原始序列中的所有信息,它的长度就成了限制模型性能的瓶颈。如机器翻译问题,当要翻译的句子较长时,一个Context可能存不下那么多信息,就会造成精度的下降,而Attention机制的提出则有利于解决这一问题。Attention 的方式有很多种计算方式,这里介绍其中的一种,软性注意力机制。
3.1 引入Attention
我们现在设Encoder的LSTM在
t
t
t 时刻输出的隐藏状态信息为
h
t
h_t
ht,Decoder的LSTM在
t
t
t 时刻输出的隐藏状态信息为
H
t
H_t
Ht,输出状态信息为
s
t
s_t
st,则上面的Decoder输出
H
t
=
f
(
H
t
−
1
,
s
t
−
1
)
H_t=f(H_{t-1},s_{t-1})
Ht=f(Ht−1,st−1)根据上面的式子,当句子过长的时候,信息会在循环神经网络的传递中逐渐消失,导致精度下降,因此,我们提出了注意力机制,即额外添加一个信息,让Decoder在句子中注意到重要的信息,设添加的信息为
C
t
C_t
Ct,则表示为
H
t
=
f
(
H
t
−
1
,
s
t
−
1
,
C
t
)
H_t=f(H_{t-1},s_{t-1},C_t)
Ht=f(Ht−1,st−1,Ct)其中
C
t
C_t
Ct 指的是在时刻
t
t
t 的上下文向量。我们把它定义为所有的原文隐藏层值
h
t
h_t
ht 加权平均的结果 ,即
C
t
=
∑
i
=
1
n
α
t
i
h
i
C_t=\sum_{i=1}^{n}\alpha_{ti}h_{i}
Ct=i=1∑nαtihi其中的
α
t
i
\alpha_{ti}
αti 就是对
t
t
t 时刻的各个原文隐藏状态
h
h
h 给到的权重,也就是注意力的大小,该权重称为全局对齐权重。
3.2 计算全局对齐权重
计算全局对齐权重的时候,我们肯定是不可能一个个权重进行人工标注的,太过于麻烦,也太过有主观性了,于是,我们可以使用一个可训练的权重
W
h
W_h
Wh 来进行计算各个隐藏状态的权重,设经过训练后的权重分数为
e
i
j
e_{ij}
eij,可以表示为
e
i
j
=
s
c
o
r
e
(
H
i
−
1
,
h
j
)
e_{ij}=score(H_{i-1},h_j)
eij=score(Hi−1,hj)由于需要输出的是权重,所以我们可以将其经过一层softmax网络,得到隐层的权重为
α
i
j
=
e
x
p
(
e
i
j
)
∑
k
=
1
n
e
x
p
(
e
i
k
)
\alpha_{ij}=\frac{exp({e_{ij}})}{\sum_{k=1}^{n}exp({e_{ik}})}
αij=∑k=1nexp(eik)exp(eij)由于
α
i
j
\alpha_{ij}
αij 与
h
j
h_j
hj 一起构成的
C
t
C_t
Ct 被代入Decoder网络中进行计算,因此
∇
f
(
C
t
)
\nabla f(C_t)
∇f(Ct) 可以进行反向传播,也因此这里的权重计算函数是可以被梯度下降优化的。
经过以上的推导,注意力机制的计算的流程已经很明显了,只剩下一个 s c o r e ( H i − 1 , h j ) score(H_{i-1},h_j) score(Hi−1,hj) 的计算是未知的,那么 e i j = s c o r e ( H i − 1 , h j ) e_{ij}=score(H_{i-1},h_j) eij=score(Hi−1,hj) 是怎么计算的呢?
e i j = s c o r e ( H i − 1 , h j ) e_{ij}=score(H_{i-1},h_j) eij=score(Hi−1,hj) 的计算称为权重计算函数,其计算的形式多种多样,主要的计算方式有如下几种:
| 种类 | 权重计算函数 | 参数含义 |
|---|---|---|
| 加性模型 | e i j = v T t a n h ( W 1 H i − 1 + W 2 h j ) e_{ij}=v^T tanh (W_1H_{i-1}+W_2h_j) eij=vTtanh(W1Hi−1+W2hj) | v , W 1 , W 2 v,W_1,W_2 v,W1,W2 是可学习参数 |
| 乘法模型 | e i j = h j W H i − 1 e_{ij}=h_jWH_{i-1} eij=hjWHi−1 | W W W 是可学习参数 |
| 点积模型 | e i j = h j T H i − 1 e_{ij}=h_j^TH_{i-1} eij=hjTHi−1 | v , W 1 , W 2 v,W_1,W_2 v,W1,W2 是可学习参数 |
| 缩放点积模型 | e i j = h j T H i − 1 d H e_{ij}=\frac{h_j^TH_{i-1}}{\sqrt{d_H}} eij=dHhjTHi−1 | d H d_H dH 为输入向量的维度 |
当输入向量的维度比较高的时候,点积模型通常有比较大的方差,从而导致Softmax函数的梯度会比较小。因此,缩放点积模型通过除以一个平方根项来平滑分数数值,也相当于平滑最终的注意力分布,缓解这个问题。
4. seq2seq加入Attention机制
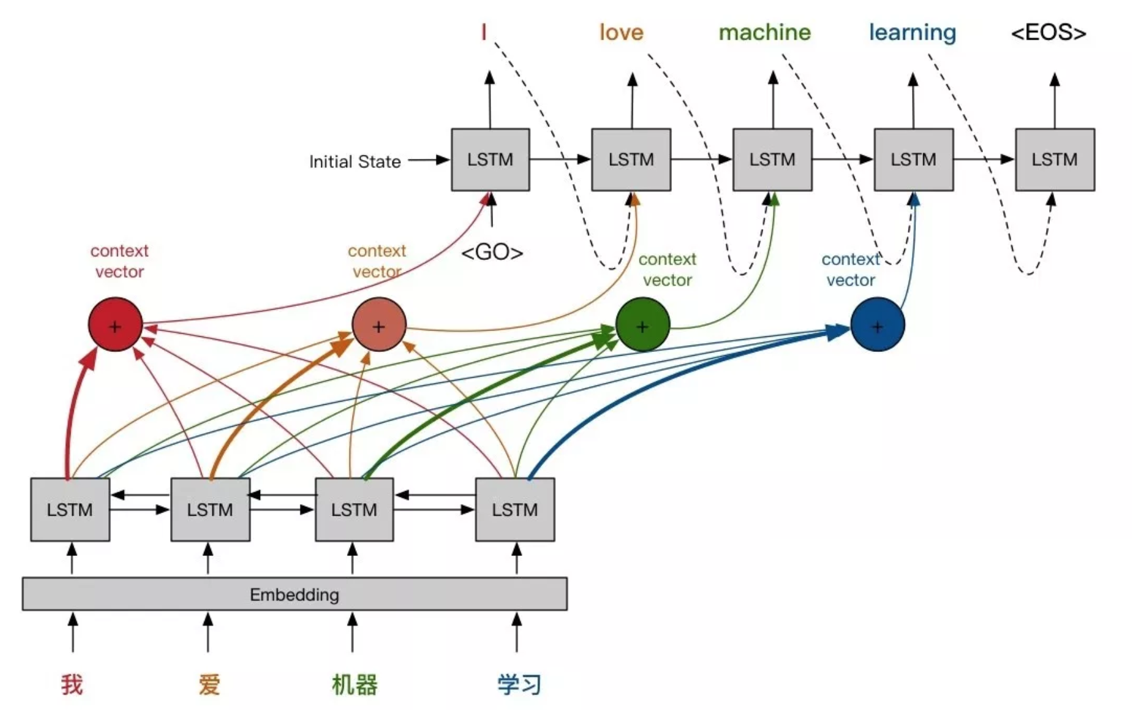
当将Attention机制加入到seq2seq模型后,模型的结构如下:
上面结构中的四个加号也就是注意力机制的参数
α
\alpha
α ,因为输入的最大长度为4,所以注意力参数也只有四个,这里的加号表示使用的是加性模型,每一个隐藏状态都会输入到每一个注意力参数当中计算权重,并将计算的参数传递到Decoder中,其计算流程如下。
设输入序列为
x
=
(
x
1
,
x
2
,
⋯
,
x
n
)
x=(x_1,x_2,\cdots,x_n)
x=(x1,x2,⋯,xn),输出序列为
y
=
(
y
1
,
y
2
,
⋯
,
y
m
)
y=(y_1,y_2,\cdots,y_m)
y=(y1,y2,⋯,ym),首先,将输入序列通过LSTM,得到最后一个状态的隐藏状态和输出状态,即
h
n
,
c
n
=
L
S
T
M
(
x
,
h
n
−
1
,
c
n
−
1
)
h_n,c_n=LSTM(x,h_{n-1},c_{n-1})
hn,cn=LSTM(x,hn−1,cn−1)之后就是计算注意力的问题了。
设
s
t
s_t
st 为解码器
t
t
t 时刻的隐层状态输出,
h
t
h_t
ht 为编码器
t
t
t 时刻的隐层状态输出,故计算解码器
i
i
i 时刻与编码器
j
j
j 时刻的权重计算函数为:
e
i
j
=
v
T
t
a
n
h
(
W
1
s
i
+
W
2
h
j
)
e_{ij}=v^T tanh (W_1s_i+W_2h_j)
eij=vTtanh(W1si+W2hj)权重系数表现如下:
α
i
k
=
e
x
p
(
e
i
k
)
∑
l
=
1
n
e
x
p
(
e
i
l
)
,
k
=
1
,
⋯
,
n
\alpha_{ik}=\frac{exp({e_{ik}})}{\sum_{l=1}^{n}exp({e_{il}})},k=1,\cdots,n
αik=∑l=1nexp(eil)exp(eik),k=1,⋯,n接着计算加上了注意力权重后的隐层状态的加权向量
c
i
c_i
ci
c
i
=
∑
j
=
1
n
α
i
j
h
j
c_i = \sum_{j=1}^{n}\alpha_{ij}h_{j}
ci=j=1∑nαijhj然后将
c
i
c_i
ci 与上一时刻解码器的输出
s
i
−
1
s_{i-1}
si−1 结合并输入到LSTM中,最后将其输出到一个softmax网络结构中,输出概率最大的标签即可。
5. 模型理解
seq2seq模型其实是一个条件语言模型,设编码器的输入是一个序列
x
1
,
x
2
,
⋯
,
x
n
x_1,x_2,\cdots,x_n
x1,x2,⋯,xn ,并输出一个编码状态
C
C
C ,解码器根据编码状态
C
C
C 输出
y
1
y_1
y1 ,再根据
y
1
,
⋯
,
y
m
−
1
y_1,\cdots,y_{m-1}
y1,⋯,ym−1输出
y
m
y_m
ym ,并组成输出序列
y
1
,
y
2
,
⋯
,
y
m
y_1,y_2,\cdots,y_m
y1,y2,⋯,ym ,则我们需要计算的概率其实就是如下的式子:
a
r
g
m
a
x
P
(
y
1
,
y
2
,
⋯
,
y
m
∣
x
1
,
x
2
,
⋯
,
x
n
)
argmaxP(y_1,y_2,\cdots,y_m|x_1,x_2,\cdots,x_n)
argmaxP(y1,y2,⋯,ym∣x1,x2,⋯,xn)即给定输入的序列,使得输出序列的概率值最大。
之后再根据最大似然估计,最大化输出序列的概率,
P
(
y
1
,
y
2
,
⋯
,
y
m
∣
x
1
,
x
2
,
⋯
,
x
n
)
=
Π
t
=
1
m
P
(
y
t
∣
y
1
,
⋯
,
y
t
−
1
,
x
1
,
x
2
,
⋯
,
x
n
)
=
Π
t
=
1
m
P
(
y
t
∣
y
1
,
⋯
,
y
t
−
1
,
C
)
\begin{aligned} &P(y_1,y_2,\cdots,y_m|x_1,x_2,\cdots,x_n) \\ =&\Pi^{m}_{t=1}P(y_t|y_1,\cdots,y_{t-1},x_1,x_2,\cdots,x_n) \\ =&\Pi^{m}_{t=1}P(y_t|y_1,\cdots,y_{t-1},C) \end{aligned}
==P(y1,y2,⋯,ym∣x1,x2,⋯,xn)Πt=1mP(yt∣y1,⋯,yt−1,x1,x2,⋯,xn)Πt=1mP(yt∣y1,⋯,yt−1,C)由于上面的公式需要计算出
P
(
y
1
∣
C
)
,
P
(
y
2
∣
y
1
,
C
)
,
⋯
P(y_1|C),P(y_2|y_1,C),\cdots
P(y1∣C),P(y2∣y1,C),⋯ ,这个概率连乘会非常非常小不利于计算存储,所以需要对公式取对数计算:
log
P
(
y
1
,
y
2
,
⋯
,
y
m
∣
x
1
,
x
2
,
⋯
,
x
n
)
=
∑
t
=
1
m
log
P
(
y
t
∣
y
1
,
⋯
,
y
t
−
1
,
C
)
\log P(y_1,y_2,\cdots,y_m|x_1,x_2,\cdots,x_n)=\sum^{m}_{t=1}\log P(y_t|y_1,\cdots,y_{t-1},C)
logP(y1,y2,⋯,ym∣x1,x2,⋯,xn)=t=1∑mlogP(yt∣y1,⋯,yt−1,C)所以这样就变成了
P
(
y
1
∣
C
)
+
P
(
y
2
∣
y
1
,
C
)
+
⋯
P(y_1|C)+P(y_2|y_1,C)+\cdots
P(y1∣C)+P(y2∣y1,C)+⋯ 概率相加的问题,这样也可以看成输出结果通过softmax就变成了概率最大,而损失最小的问题,输出序列损失最小化。
6. 模型细节
以上就是seq2seq模型加入Attention机制的全国过程,但是,这些过程中还有一些细节在实现的时候需要注意。
6.1 解码器结构
编码器的结构没什么好说的,几乎所有的编码器结构都是上面的一种结构,即经过LSTM获得隐藏状态与输出状态的向量,但是,解码器作为处理中间向量的结构,却有很多种形式,下面我来介绍几种常见的形式,为简单起见,这里就不画注意力向量的结构了。
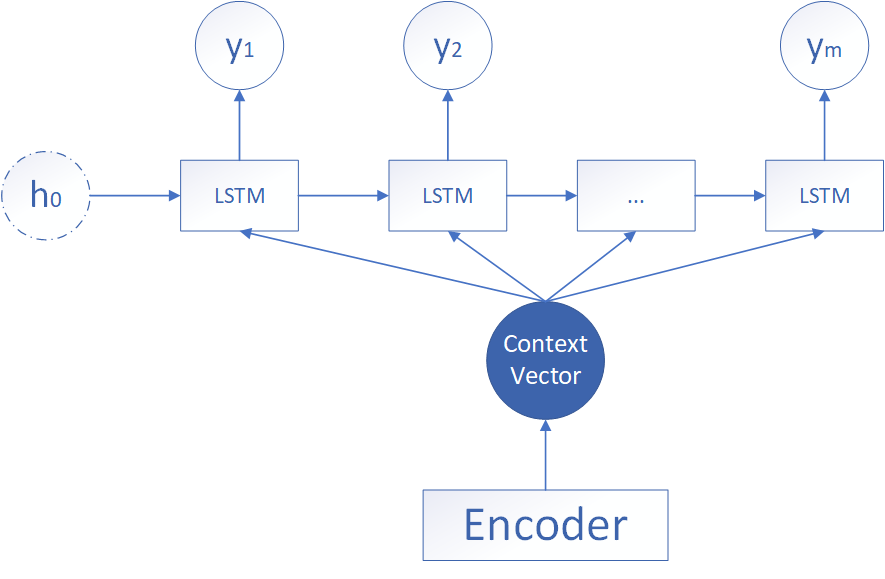
-
中间向量直接传入
该形式的结构如上所示,Encoder获得了中间向量后,将中间向量直接当做第一个LSTM的初始状态并输入,后面的时间步只接受上一个LSTM的隐藏状态的参数,设中间向量符号为 c c c,Decoder在 t t t 时刻的隐藏状态和输出状态分别为 h t , y t h_t,y_t ht,yt ,则该情况的公式计算如下:
h 1 = σ ( W 1 c + b 1 ) h t = σ ( W t 1 h t − 1 + b t 1 ) y t = σ ( W t 2 h t + c ) \begin{aligned} h_1&=\sigma(W_1c+b_1) \\ h_t &= \sigma(W_{t1}h_{t-1}+b_{t1}) \\ y_t&=\sigma(W_{t2}h_t+c) \end{aligned} h1htyt=σ(W1c+b1)=σ(Wt1ht−1+bt1)=σ(Wt2ht+c)其中 W 1 , W t 1 , W t 2 W_1,W_{t1},W_{t2} W1,Wt1,Wt2 为可学习的参数, b 1 , b t 1 , b t 2 b_1,b_{t1},b_{t2} b1,bt1,bt2 为可学习的偏置。 -
中间向量加入每一个状态
该形式的结构如上所示,第二种的形式有自己初始的隐藏状态 h 0 h_0 h0,一般是随机初始化的参数,而对于中间向量,则将其当成每一个时间步的LSTM的输入,可以看到在 Decoder 的每一个神经元都拥有相同的输入 c c c,该形式的计算公式如下:
h t = σ ( W 1 h t − 1 + W 2 c + b t ) y t = σ ( W 3 h t + c ) \begin{aligned} h_t&=\sigma(W_1h_{t-1}+W_2c+b_t) \\ y_t&=\sigma(W_3h_t+c) \end{aligned} htyt=σ(W1ht−1+W2c+bt)=σ(W3ht+c) -
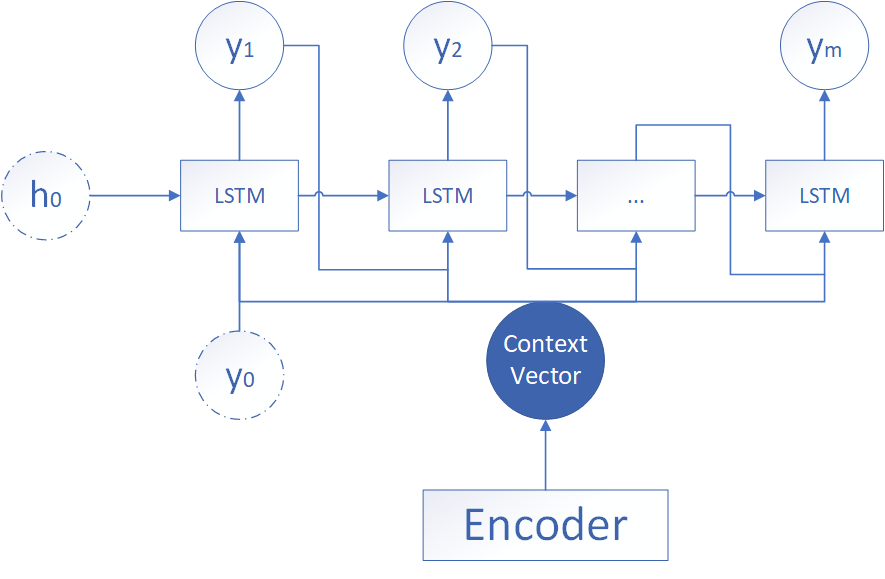
将输出一并加入到下一个时间步的输出
该形式的结构如上所示,该情况与第二种情况类似,但是在输入方面,多了一个上一个神经元的输出。即每一个神经元的输入包括:上一个神经元的隐藏层向量,上一个神经元的输出 ,编码器的中间向量。计算方式如下:
h t = σ ( W 1 c + W 2 h t − 1 + W 3 y t − 1 + b t ) y t = σ ( W 4 h t + c ) \begin{aligned} h_t&=\sigma(W_1c+W_2h_{t-1}+W_3y_{t-1}+b_t) \\ y_t&=\sigma(W_4h_t+c) \end{aligned} htyt=σ(W1c+W2ht−1+W3yt−1+bt)=σ(W4ht+c)
6.2 加入信息方式
经过上面的步骤,你一定发现不管是加入注意力机制的向量还是使用不同形式的解码器,都会有多个输入的信息加入到不同的时间步中,但是,LSTM的输入只有一个,我们应该怎样将不同的输入信息都输入到LSTM中呢?
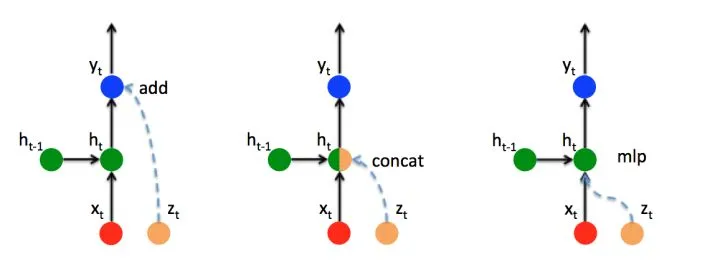
常见的处理多个信息输入的方式有三种,这里我们以注意力机制得到的向量与上一个时间步的向量相结合为例。
这里设上一个时间步的隐藏状态为
h
t
−
1
h_{t-1}
ht−1,
z
t
z_t
zt 为额外加入的注意力向量。
- ADD
第一种方法直接而将额外的向量加入到输出上,形式如下:
y t = y t + z t y_t=y_t+z_t yt=yt+zt
2.CONTAC
第二种方法将原来计算得到的 h t h_t ht 与新加入的信息 z t z_t zt 两个向量拼接起来,但是直接拼接会导致向量的维度扩大,如果想要将向量恢复到原来的维度,那么需要乘一个权重向量 W c W_c Wc ,表示如下:
h t = W c [ h t , z t ] h_t=W_c[h_{t},z_t] ht=Wc[ht,zt]
3.MLP
新添加一个对 z t z_t zt 的感知单元,即 h z t = W z t z t + b z t h_{zt}=W_{zt}z_t+b_{zt} hzt=Wztzt+bzt,这样,输出的公式即为:
h t = σ ( ( W z t z t + b z t ) + ( W x t x t + b x t ) + ( W h t h t − 1 + b h t ) ) \begin{aligned} h_t&=\sigma((W_{zt}z_t+b_{zt})+(W_{xt}x_t+b_{xt})+(W_{ht}h_{t-1}+b_{ht})) \end{aligned} ht=σ((Wztzt+bzt)+(Wxtxt+bxt)+(Whtht−1+bht))
参考文章
[1] : https://baijiahao.baidu.com/s?id=1650496167914890612&wfr=spider&for=pc
[2] : https://zhuanlan.zhihu.com/p/51383402
[3] : https://zhuanlan.zhihu.com/p/380892265
[4] : https://blog.csdn.net/CSTGYinZong/article/details/126245369
[5] : https://www.bilibili.com/video/BV1LD4y1P7nK?p=90