15.子空间投影

用途：用于在$A\vec{x}=\vec{b}$无解（即$\vec{b}$不属于$A$的列空间）时，将$\vec{b}$投影至$A$的列空间，从而得到一个最接近的解$\hat{\vec{x}}$

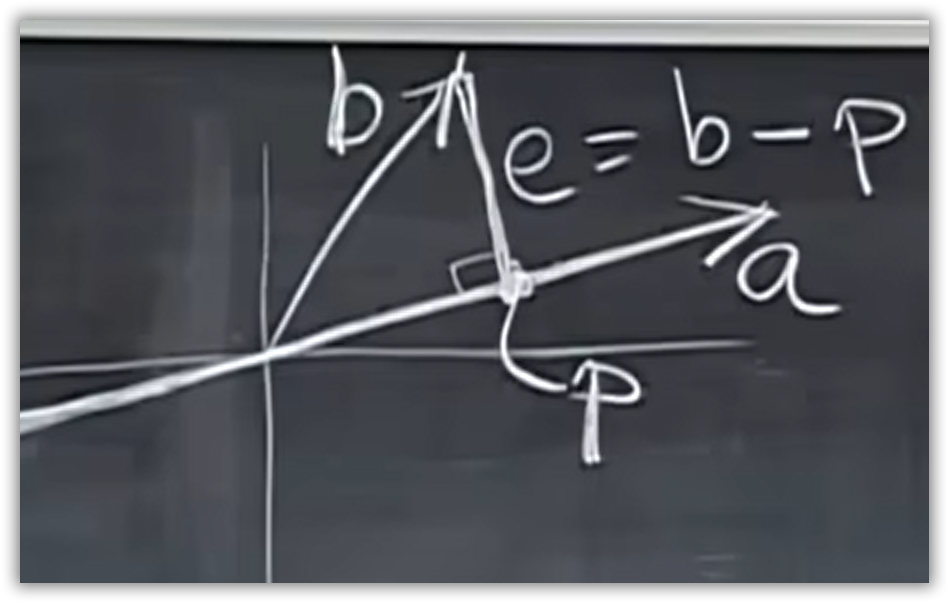
1. 考虑向量投影至向量
   
   设$\vec{p}=x\vec{a}$

   因为$\vec{e}\perp \vec{a}$，即$\vec{e}$与$\vec{a}$正交，所以${\vec{a}}^T\vec{e}={\vec{a}}^T(\vec{b}-x\vec{a})=0$

   化简得${\vec{a}}^T\vec{b}={\vec{a}}^T\vec{a}x$,，又${\vec{a}}^T\vec{a}$为一个常数，左右同除${\vec{a}}^T\vec{a}$得到$x=\frac{{\vec{a}}^T\vec{b}}{{\vec{a}}^T\vec{a}}$

   $\therefore \vec{p}=\vec{a}\frac{{\vec{a}}^T\vec{b}}{{\vec{a}}^T\vec{a}}$，其中$\vec{b}$翻倍则$\vec{p}$翻相同倍数，$\vec{a}$翻倍则$\vec{p}$不变

   由此可知对矩阵$\vec{b}$进行操作得到了$\vec{p}$

   将操作所用矩阵（即用于生成投影的矩阵）称为投影矩阵，记作$P$，那么$P=\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}},\vec{p}=P\vec{b}$

   • $P$的秩为$1$（$P$中各行均为$a^T$的倍数），且$P$的列空间即为$\vec{a}$所在直线，$\vec{a}$是$P$的一个基

   • $\vec{b}$与$\vec{a}$共线时，$\vec{p}=\vec{b}$

     证明： ①图像说明

     ​    ②设$\vec{b}=y\vec{a}$，$\vec{p}=P\vec{b}=y\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}\vec{a}=y\vec{a}=\vec{b}$

   • $P$为对称矩阵

     证明：$P=\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}$，而$\vec{a}{\vec{a}}^T$为对称矩阵，${\vec{a}}^T\vec{a}$为一个常数

   • $P^2=P$

     证明： ①用图像可说明$PP\vec{b}=P\vec{b}$从而得证

     ​    ②$P^2=\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}\cdot \frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}=\frac{\vec{a}{\vec{a}}^T\vec{a}{\vec{a}}^T}{({\vec{a}}^T\vec{a}{)}^2}=\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}=P$

2. 考虑向量投影至平面
   
   设 { a ⃗ 1 , a ⃗ 2 } \{\vec{a}_1 , \vec{a}_2\} {a 1​,a 2​}为平面的一组基，该平面可表示为矩阵$A=\left[\begin{array}{cc}{\vec{a}}_1& {\vec{a}}_2\end{array}\right]$的列空间，$\vec{p}=x_1{\vec{a}}_1+x_2{\vec{a}}_2=A\vec{x}$

   因为$\vec{e}=\vec{b}-\vec{p}$垂直于平面，所以$\vec{e}\perp {\vec{a}}_1,\vec{e}\perp {\vec{a}}_2$

   $\therefore \{\begin{array}{c}{\vec{a}}_1^T(\vec{b}-A\vec{x})=0\\ {\vec{a}}_2^T(\vec{b}-A\vec{x})=0\end{array}$，即$\left[\begin{array}{c}{\vec{a}}_1^T\\ {\vec{a}}_2^T\end{array}\right](\vec{b}-A\vec{x})=\left[\begin{array}{c}0\\ 0\end{array}\right]$，即$A^T(\vec{b}-A\vec{x})=\vec{0}$

   化简得：$A^T\vec{b}=A^{T}A\vec{x}$，因而$\vec{x}=(A^{T}A{)}^{-1}{A}^T\vec{b}$（由第$5$节的证明可知$A^{T}A$可逆）

   $\therefore \vec{p}=A\vec{x}=A(A^{T}A{)}^{-1}{A}^T\vec{b}$

   $\therefore P=A(A^{T}A{)}^{-1}{A}^T$

   由原理及计算过程可以知道$A$一定要列满秩

   设$A$有$m$行$n$列

   • $P$与$A$的列空间一致

     证明： ①$\vec{p}=P\vec{b}$可表示$P$列空间中的所有向量，且$\vec{p}$可能为$A$列空间中任何向量，因而二者列空间一致

     ​    ②$P=A(A^{T}A{)}^{-1}{A}^T$，其中$(A^{T}A{)}^{-1}$是一个$n$行$n$列的可逆矩阵，行满秩，而$A^T$也行满秩，因而$(A^{T}A{)}^{-1}{A}^T$行满秩且有$n$个主列

     ​ 又$A$各列线性无关，因而想得到$P$中的任意列，均分别对$A$各列只有一种线性组合方式，这些方式之间 的线性关系与$(A^{T}A{)}^{-1}{A}^T$中各列的线性关系一致，所以$(A^{T}A{)}^{-1}{A}^T$的主列在$P$中的对应列也是主列 且$P$只有这$n$个主列

     ​ 又$P$的主列均由$A$的各列线性组合而来且$A$中各列均参与组合（$(A^{T}A{)}^{-1}{A}^T$行满秩，不存在$0$行，所以 $A$不会有任何一列不参与组合），因而$P$与$A$的列空间一致

   • 此时若$A$是方阵，则$P=I$

     证明： ①$A$为方阵时，其列空间为整个$m$维空间，包括$\vec{b}$，因而$\vec{b}$的投影即为其本身

     ​    ②$P=A(A^{T}A{)}^{-1}{A}^T=A{A}^{-1}(A^T{)}^{-1}{A}^T=I$

   • $P$为对称矩阵

     证明：$P^T=A((A^{T}A{)}^{-1}{)}^T{A}^T=A((A^{T}A{)}^T{)}^{-1}{A}^T=A(A^{T}A{)}^{-1}{A}^T=P$

   • $P^2=P$

     证明： ①用图像可说明$PP\vec{b}=P\vec{b}$从而得证

     ​    ②$P^2=A(A^{T}A{)}^{-1}{A}^{T}A(A^{T}A{)}^{-1}{A}^T=A((A^{T}A{)}^{-1}{A}^{T}A)(A^{T}A{)}^{-1}{A}^T=A(A^{T}A{)}^{-1}{A}^T=P$

3. 个人理解

   将一个向量投影到一个空间本质上相当于在空间中尽可能表示出原向量，或者说在原向量中删去与空间正交的部分

   依几何意义可知投影矩阵一定不可逆

打赏

制作不易，若有帮助，欢迎打赏！