一、EM算法的提出

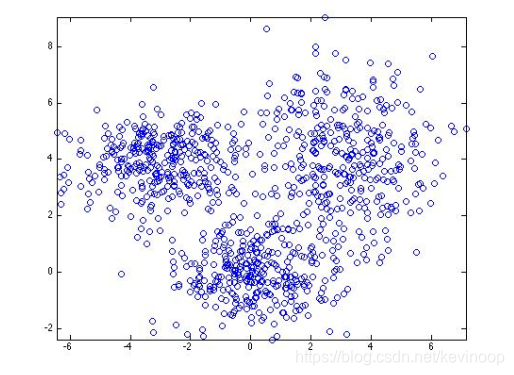
当你有一组数据像如下这样：

Note: picture source

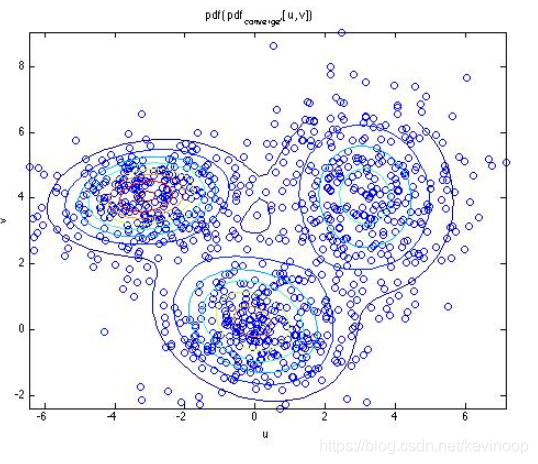
显然用单个高斯分布模型去拟合它们效果不好，这是一个典型的高斯混合模型的例子：
$$p(X)=\sum _{l=1}^k{\alpha }_{l}N(X|{\mu }_l,{\Sigma }_l)\sum _{l=1}^k{\alpha }_l=1$$$$（其中{\alpha }_l可以理解为每一个高斯分布的权重）$$
令 Θ = { α 1 , … , α k , μ 1 , … , μ k , Σ 1 , … , Σ k } \Theta=\{\alpha_1,\ldots,\alpha_k,\mu_1,\ldots,\mu_k,\Sigma_1,\ldots,\Sigma_k\} Θ={α1​,…,αk​,μ1​,…,μk​,Σ1​,…,Σk​}，则有：

$$\begin{gathered} {\Theta }_{MLE}={\mathrm{argmax}}_{\Theta }L(\Theta |X) \\ ={\mathrm{argmax}}_{\Theta }\left(\sum _{i=1}^{n}log\sum _{l=1}^k{\alpha }_{l}N(X|{\mu }_l,{\Sigma }_l)\right) \end{gathered}$$

该式子包含和（或积分）的对数，不能像单个高斯模型那样直接求导，再令导数为0来求解。这时我们需要利用 EM 算法通过迭代逐步近似极大化 $L(\Theta |X)$ 来求解。

Note: picture source

二、EM算法的导出

先提出 Jensen 不等式：
对于凸函数(convex)，有：
$$f(t\cdot x_1+(1-t)\cdot x_2)\le t\cdot f(x_1)+(1-t)\cdot f(x_2)$$扩展到高维，令 ${\sum }_{i=1}^k{p}_i=1p_i\ge 0$：
$$f(p_1\cdot x_1+\dots +p_k\cdot x_k)\le p_1\cdot f(x_1)+\dots +p_k\cdot f(x_k)$$$$f(\sum _{i=1}^k{p}_i\cdot x_i)\le \sum _{i=1}^k{p}_i\cdot f(x_i)$$用 $\varphi$ 代替 $f$ ， $f(x)$ 代替 $x$， 我们有
$$\varphi (\sum _{i=1}^k{p}_i\cdot f(x_i))\le \sum _{i=1}^k{p}_i\cdot \varphi (f(x_i))$$

故对于凸函数(convex)，有下面这条结论：
$$\varphi (E[f(x)])\le E[\varphi (f(x))]$$ 同理，对于凹函数(concave)，有相反的结论：
$$\varphi (E[f(x)])\ge E[\varphi (f(x))]$$

我们通过引入隐变量 Z 来极大化观测数据 X 关于参数 $\theta$ 的对数似然函数：
$$\begin{gathered} L(\theta )=lnP(X|\theta )=ln\left(\frac{P(X,Z|\theta )}{P(Z|X,\theta )}\right) \\ =ln\left(\frac{P(X,Z|\theta )}{Q(Z)}\cdot \frac{Q(Z)}{P(Z|X,\theta )}\right) \\ =ln\left(\frac{P(X,Z|\theta )}{Q(Z)}\right)+ln\left(\frac{Q(Z)}{P(Z|X,\theta )}\right) \end{gathered}$$

故：
$$\begin{gathered} lnP(X|\theta )={\int }_{Z}ln\left(\frac{P(X,Z|\theta )}{Q(Z)}\right)Q(Z)+{\int }_{Z}ln\left(\frac{Q(Z)}{P(Z|X,\theta )}\right)Q(Z) \\ =r(X|\theta )+KL(Q(Z)||P(Z|X,\theta )) \end{gathered}$$

其中，$KL(\cdot )\ge 0$，则 $lnP(X|\theta )\ge r(X|\theta )$，也可利用上面的 Jensen 不等式证明:
$$\begin{gathered} lnP(X|\theta )=ln{\int }_{Z}P(X,Z|\theta ) \\ =ln{\int }_Z\frac{P(X,Z|\theta )}{Q(Z)}\cdot Q(Z)=ln{E}_{Q(Z)}[f(Z)] \\ \ge E_{Q(Z)}ln[f(Z)]={\int }_{Z}ln\left(\frac{P(X,Z|\theta )}{Q(Z)}\right)\cdot Q(Z) \end{gathered}$$
又当 $Q(Z)=P(Z|X,{\Theta }^{(g)})$ 时 ，有 $KL(\cdot )=0$，此时有：
$$lnP(X|{\Theta }^{(g)})=r(X|{\Theta }^{(g)})$$
由上 $r(X|\Theta )$ 是 $L(\Theta )$ 的一个下界函数，我们通过不断求解下界函数的极大化来逼近求解对数似然函数的极大化:

$$\begin{gathered} {\Theta }^{(g+1)}={\mathrm{argmax}}_{\Theta }{\int }_{Z}ln\left(\frac{P(X,Z|\Theta )}{P(Z|X,{\Theta }^{(g)})}\right)P(Z|X,{\Theta }^{(g)}) \\ ={\mathrm{argmax}}_{\Theta }{\int }_{Z}ln\left(P(X,Z|\Theta )\right)P(Z|X,{\Theta }^{(g)})dz \end{gathered}$$

EM算法每次迭代包含两步：E步，求期望；M步，求极大化。令 ：$$Q(\Theta ,{\Theta }^{(g)})={\int }_{Z}ln\left(P(X,Z|\Theta )\right)P(Z|X,{\Theta }^{(g)})dz$$
EM算法如下：

EM算法:
输入：观测变量数据X，隐变量数据Z，联合分布 $P(X,Z|\Theta )$ ，条件分布 $P(Z|X,\Theta )$
输出：模型参数 $\Theta$
(1) 选择初始参数 ${\Theta }^{(0)}$；
(2) E步，记 ${\Theta }^{(i)}$ 为第 i 次迭代参数 $\Theta$ 的估计值，在第 i+1 次迭代的E步， 计算 $Q(\Theta ,{\Theta }^{(g)})$;
(3) M步，确定第 i+1 次迭代的参数的估计值 ${\Theta }^{(i+1)}$，即：
$${\Theta }^{(i+1)}={\mathrm{argmax}}_{\Theta }Q(\Theta ,{\Theta }^{(g)})$$
(4) 重复(2)步和(3)步，直到收敛。

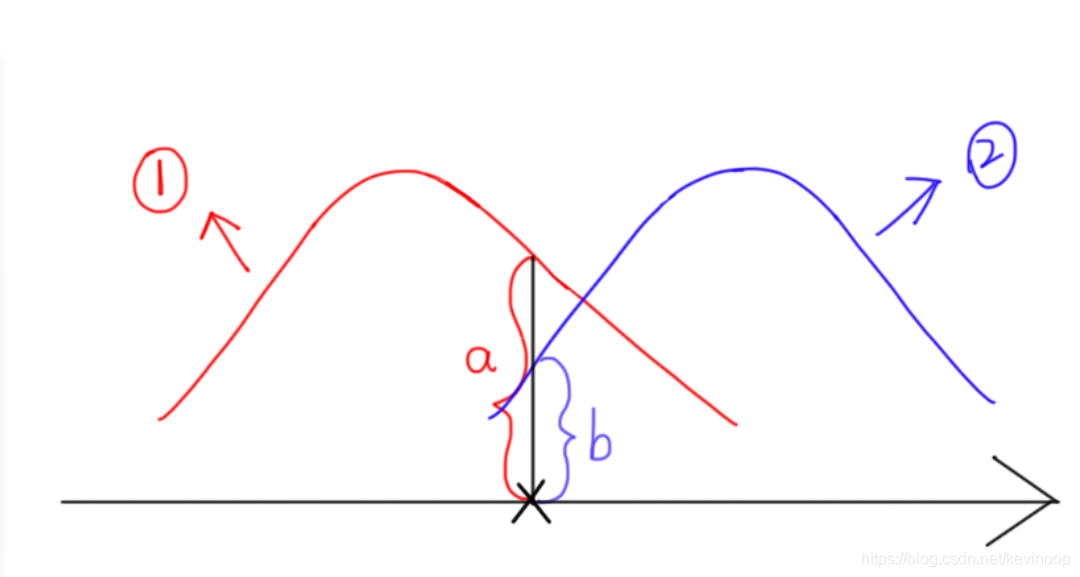
下图给出 EM 算法的直观解释：

由图，两个函数在 $\theta ={\theta }^{(g)}$ 处相等，由EM算法 (3) 步，我们得到下一个点 ${\theta }^{(g+1)}$ 使下界函数极大化。下界函数的增加保证对数似然函数在每次迭代中也是增加的。EM算法在点 ${\theta }^{(g+1)}$ 处重新计算 $Q(\Theta ,{\Theta }^{(g+1)})$， 进行下一次迭代。迭代过程中，对数似然函数不断增大，但从图可以看出EM算法不能保证找到全局最优值。

三、EM算法的收敛性

由 $$P(X|\theta )=\frac{P(X,Z|\theta )}{P(Z|X,\theta )}$$取对数有：
$$logP(X|\theta )=logP(X,Z|\theta )-logP(Z|X,\theta )$$
记，$$Q(\theta ,{\theta }^{(g)})={\int }_{Z}log\left(P(X,Z|\theta )\right)P(Z|X,{\theta }^{(g)})dz$$ $$H(\theta ,{\theta }^{(g)})={\int }_{Z}log\left(P(Z|X,\theta )\right)P(Z|X,{\theta }^{(g)})dz$$
于是对数似然函数可以写成：
$$logP(X|\theta )=Q(\theta ,{\theta }^{(g)})-H(\theta ,{\theta }^{(g)})$$
故有如下等式：
$$logP(X|{\theta }^{(g+1)})-logP(X|{\theta }^{(g)})=[Q({\theta }^{(g+1)},{\theta }^{(g)})-Q({\theta }^{(g)},{\theta }^{(g)})]-[H({\theta }^{(g+1)},{\theta }^{(g)})-H({\theta }^{(g)},{\theta }^{(g)})]$$
显然，右端第一项，由于 ${\theta }^{(g+1)}$ 使 $Q(\theta ,{\theta }^{(g)})$达到极大，所以有：
$$Q({\theta }^{(g+1)},{\theta }^{(g)})-Q({\theta }^{(g)},{\theta }^{(g)})\ge 0$$其第二项，有：
$$\begin{gathered} H({\theta }^{(g+1)},{\theta }^{(g)})-H({\theta }^{(g)},{\theta }^{(g)}) \\ ={\int }_{Z}ln\left(\frac{P(Z|X,{\theta }^{(g+1)})}{P(Z|X,{\theta }^{(g)})}\right)P(Z|X,{\theta }^{(g)}) \\ \le ln{\int }_Z\left(\frac{P(Z|X,{\theta }^{(g+1)})}{P(Z|X,{\theta }^{(g)})}P(Z|X,{\theta }^{(g)})\right) \\ =ln({\int }_{Z}P(Z|X,{\theta }^{(g+1)}))=0 \end{gathered}$$综上，有: $$logP(X|{\theta }^{(g+1)})\ge logP(X|{\theta }^{(g)})$$

四、EM算法在GMM中的应用

在本文的第一部分已经提出高斯混合模型：
$$p(X)=\sum _{l=1}^k{\alpha }_{l}N(X|{\mu }_l,{\Sigma }_l)\sum _{l=1}^k{\alpha }_l=1$$令 Θ = { α 1 , … , α k , μ 1 , … , μ k , Σ 1 , … , Σ k } \Theta=\{\alpha_1,\ldots,\alpha_k,\mu_1,\ldots,\mu_k,\Sigma_1,\ldots,\Sigma_k\} Θ={α1​,…,αk​,μ1​,…,μk​,Σ1​,…,Σk​}

在本文的第三部分我们已经推导出EM算法：
$${\Theta }^{(g+1)}={\mathrm{argmax}}_{\Theta }{\int }_{Z}ln\left(P(X,Z|\Theta )\right)P(Z|X,{\Theta }^{(g)})dz$$

E step:

我们需要定义这两项 $lnP(X,Z|\Theta )$ 和 $ P(Z|X,\Theta)$;
$$P(X|\Theta )=\sum _{l=1}^k{\alpha }_{l}N(X|{\mu }_l,{\Sigma }_l)=\prod _{i=1}^n\sum _{l=1}^k{\alpha }_{l}N(x_i|{\mu }_l,{\Sigma }_l)$$
由上式，我们可以定义：
$$\begin{gathered} P(X,Z|\Theta )=\prod _{i=1}^{n}p(x_i,z_i|\Theta ) \\ =\prod _{i=1}^{n}p(x_i|z_i,\Theta )p(z_i|\Theta )=\prod _{i=1}^n{\alpha }_{z_i}N({\mu }_{z_i},{\Sigma }_{z_i}) \end{gathered}$$
由贝叶斯公式，我们有：
$$P(Z|X,\Theta )=\prod _{i=1}^{n}p(z_i|x_i,\Theta )=\prod _{i=1}^n\frac{{\alpha }_{z_i}N({\mu }_{z_i},{\Sigma }_{z_i})}{{\sum }_{l=1}^k{\alpha }_{l}N({\mu }_l,{\Sigma }_l)}$$
结合两式，得到：
$$\begin{gathered} Q(\Theta ,{\Theta }^{(g)})={\int }_{Z}ln\left(P(X,Z|\Theta )\right)P(Z|X,{\Theta }^{(g)})dz \\ ={\int }_{z_1}\dots {\int }_{z_k}\left(\sum _{i=1}^n[ln{\alpha }_{z_i}+lnN({\mu }_{z_i},{\Sigma }_{z_i})]\right)\cdot \prod _{i=1}^{n}p(z_i|x_i,{\Theta }^{(g)})d{z}_1\dots d{z}_k \end{gathered}$$
令： $$f(z_i)=ln{\alpha }_{z_i}+lnN({\mu }_{z_i},{\Sigma }_{z_i})$$$$p(z_1,\dots ,z_k)=\prod _{i=1}^{n}p(z_i|x_i,{\Theta }^{(g)})$$ 又可以写成如下形式：
$$Q(\Theta ,{\Theta }^{(g)})={\int }_{z_1}\dots {\int }_{z_k}\left(\sum _{i=1}^{n}f(z_i)\right)\cdot p(z_1,\dots ,z_k)d{z}_1\dots d{z}_k$$看上式的第一项，可以作如下化简：
$$\begin{gathered} {\int }_{z_1}\dots {\int }_{z_k}\left(f(z_1)\right)\cdot p(z_1,\dots ,z_k)d{z}_1\dots d{z}_k \\ ={\int }_{z_1}f(z_1){\int }_{z_2}\dots {\int }_{z_k}\cdot p(z_1,\dots ,z_k)d{z}_1\dots d{z}_k \\ ={\int }_{z_1}f(z_1)\cdot p(z_1)d{z}_1 \end{gathered}$$
每一项都作类似的化简，我们得到：
$$\begin{gathered} Q(\Theta ,{\Theta }^{(g)})=\sum _{i=1}^n{\int }_{z_i}f(z_i)\cdot p(z_i)d{z}_i \\ =\sum _{i=1}^n{\int }_{z_i}\left(ln{\alpha }_{z_i}+lnN(x_i|{\mu }_{z_i},{\Sigma }_{z_i})\right)\cdot p(z_i|x_i,{\Theta }^{(g)})d{z}_i \\ =\sum _{z_i=1}^k\sum _{i=1}^n\left(ln{\alpha }_{z_i}+lnN(x_i|{\mu }_{z_i},{\Sigma }_{z_i}\right)\cdot p(z_i|x_i,{\Theta }^{(g)}) \\ =\sum _{l=1}^k\sum _{i=1}^n\left(ln{\alpha }_l+lnN(x_i|{\mu }_l,{\Sigma }_l\right)\cdot p(l|x_i,{\Theta }^{(g)}) \end{gathered}$$

M step:

$$\begin{gathered} Q(\Theta ,{\Theta }^{(g)})=\sum _{l=1}^k\sum _{i=1}^n\left(ln{\alpha }_l+lnN(x_i|{\mu }_l,{\Sigma }_l)\right)\cdot p(l|x_i,{\Theta }^{(g)}) \\ =\sum _{l=1}^k\sum _{i=1}^{n}ln{\alpha }_l\cdot p(l|x_i,{\Theta }^{(g)}) \\ +\sum _{l=1}^k\sum _{i=1}^{n}ln[N(x_i|{\mu }_l,{\Sigma }_l)]\cdot p(l|x_i,{\Theta }^{(g)}) \end{gathered}$$
容易看出第一项只含参数 $\alpha$，第二项只含参数 $\mu ,\Sigma$，因此我们可以独立地进行最大化两项。
（1）最大化 $\alpha$
$$\frac{\partial {\sum }_{l=1}^k{\sum }_{i=1}^{n}ln{\alpha }_l\cdot p(l|x_i,{\Theta }^{(g)})}{\partial {\alpha }_1,\dots ,\partial {\alpha }_k}=[0,\dots ,0]$$$$st.\sum _{l=1}^k{\alpha }_l=1$$
这是一个有约束的极值问题，我们利用拉格朗日乘子法进行求解：
$$L({\alpha }_1,\dots ,{\alpha }_k,\lambda )=\sum _{l=1}^{k}ln({\alpha }_l)\left(\sum _{i=1}^{n}p(l|x_i,{\Theta }^{(g)}\right)-\lambda \left(\sum _{l=1}^k{\alpha }_l-1\right)$$ 求解如下：
$$\Rightarrow \frac{\partial L}{\partial {\alpha }_l}=\frac{1}{{\alpha }_l}\left(\sum _{i=1}^{n}p(l|x_i,{\Theta }^{(g)})\right)-\lambda =0$$$$\frac{\partial L}{\partial \lambda }=\left(\sum _{l=1}^k{\alpha }_l-1\right)=0$$$$\Rightarrow {\alpha }_l=\frac{1}{N}\sum _{i=1}^{n}p(l|x_i,{\Theta }^{(g)})$$

由下图我们可以直观理解：
${\alpha }_1$ 就是把所有样本点的 $\frac{a}{a+b}$ 加起来再除以样本总数N，即求所有样本点的 $\frac{a}{a+b}$ 的均值；
${\alpha }_2$ 就是把所有样本点的 $\frac{b}{a+b}$ 加起来再除以样本总数N，即求所有样本点的 $\frac{b}{a+b}$ 的均值；

（2）最大化 $\mu ,\Sigma$
$$\frac{\partial {\sum }_{l=1}^k{\sum }_{i=1}^{n}ln[N(x_i|{\mu }_l,{\Sigma }_l)]\cdot p(l|x_i,{\Theta }^{(g)})}{\partial {\mu }_1,\dots ,\partial {\mu }_k,\partial {\Sigma }_1,\dots ,\partial {\Sigma }_k}=[0,\dots ,0]$$
经过化简可以得到：
$${\mu }_l=\frac{{\sum }_{i=1}^n{x}_{i}p(l|x_i,\Theta )}{{\sum }_{i=1}^{n}p(l|x_i,\Theta )}$$
$${\Sigma }_l=\frac{{\sum }_{i=1}^n(x_i-{\mu }_l)(x_i-{\mu }_l{)}^{T}p(l|x_i,\Theta )}{{\sum }_{i=1}^{n}p(l|x_i,\Theta )}$$

五、PYTHON Demos

Demo1:

Demo2:

——————————代码链接——————————

六、参考资料

[1] 李航《统计学习方法》
[2] 徐亦达教授的自视频
[3] machine-learning-notes(em.pdf).Professor Richard Xu .