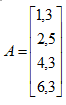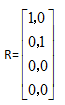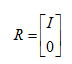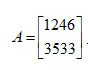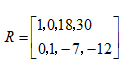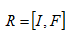求解AX=b,
首先,之前说过的,如何保证AX=b有解
两种说法,1,b是A中各列向量线性组合(b在A的列空间中)2,在如果方程左侧消元得到某行全部为0,那么与之对应的b随着左侧消元也要变为0.
AX=b的解由特解Xp加上零空间的任意向量Xn,也就是我们所说的通解X=Xp+Xn
原因是AXp=b,AXn=0,A(Xp+Xn)=b
m by n matrix A of rank r,m*n的矩阵的秩r(秩的个数就是主元的个数),那么可知,r<=m,r<=n。
列满秩(列的个数小于行的个数)(每一列都有一个主元)
r=n,A的零空间N(A)只有零向量(AX=0的解只有零向量),AX=b的解X=Xp
解释:列满秩的矩阵没有自由变量 有一个解或没有解
举例
经过消元将其变为最简式
RX=0写成方程形式也就是x1=0,x2=0.因此说AX=0的解只有零向量,AX=b的解也因此只有Xp
我们将这个结果扩展到所有的列满秩的矩阵,经过消元得到的是
行满秩(行的个数小于列的个数)(每一行都有一个主元)
r=m,那么不管b为多少,都有解,AX=0的解不只有零向量
解释:行满秩的矩阵有m个主变量,n-m个自由量
举例
经过消元将其变为最简式
没有0行,不管b为多少,都有解
扩展到所有的行满秩的矩阵,经过消元得到的是
r=m=n,AX=0的解只有零向量,AX=b只有一个解
这样的矩阵经过消元变为单位矩阵I
总结
r=m<n,R=[I F],有无穷个解
r=n<m
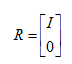
r=m=n,R=I,只有一个解
r<m<n,有0个解或无穷个解。