一,题目链接
(市赛题目,涉侵权联系删)
二,题目分析
(一)查壳
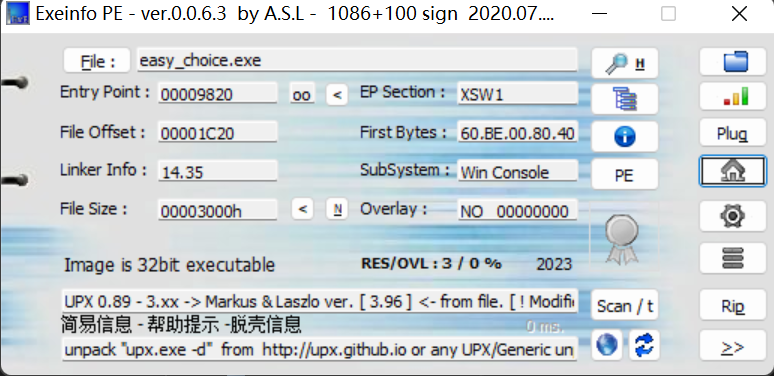
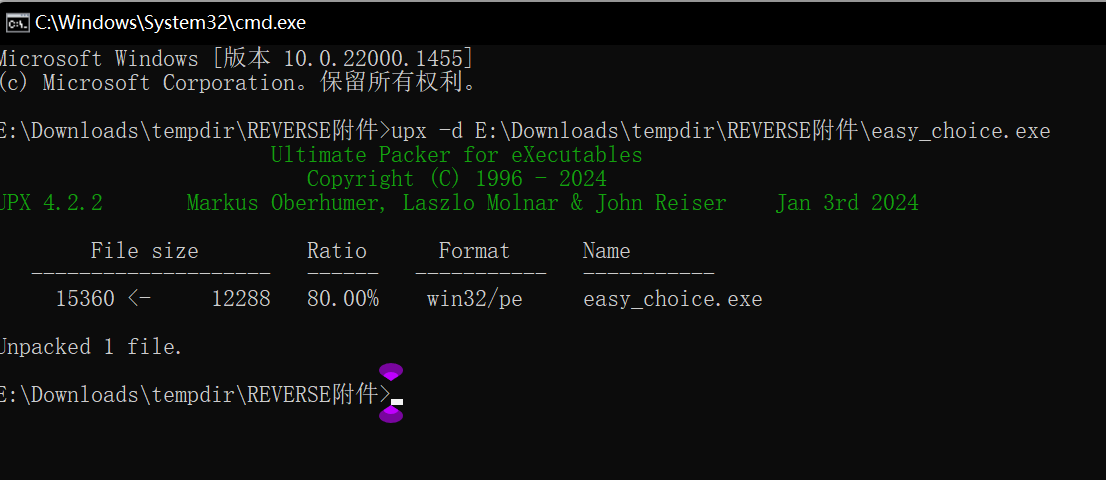
查壳带upx壳,32位
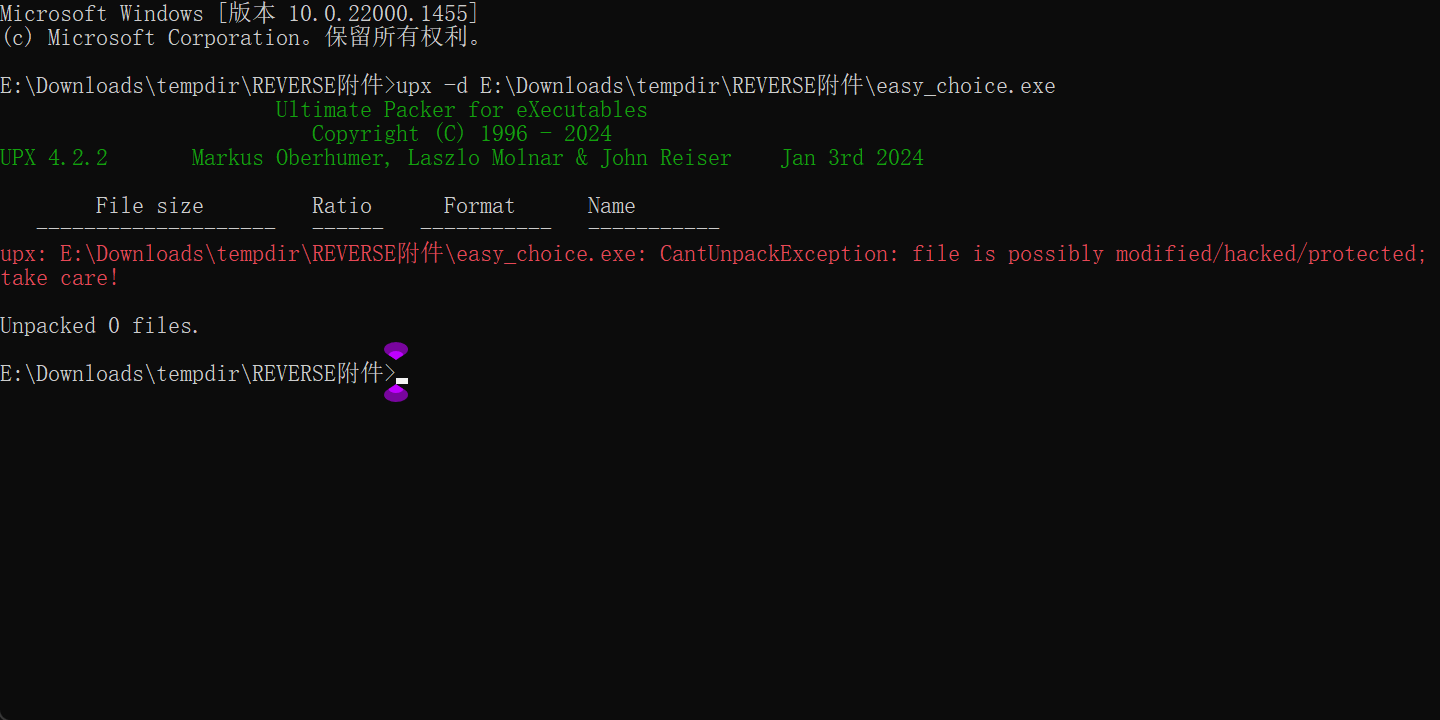
用工具脱壳,发现脱不了,说明upx的壳特征被魔改
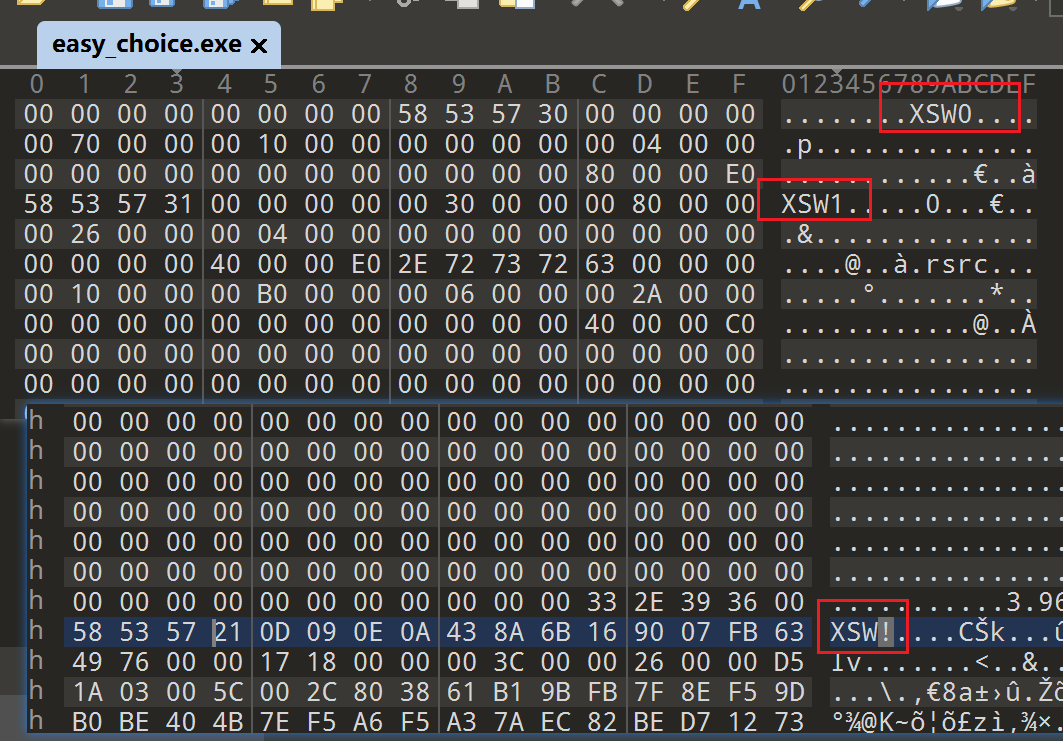
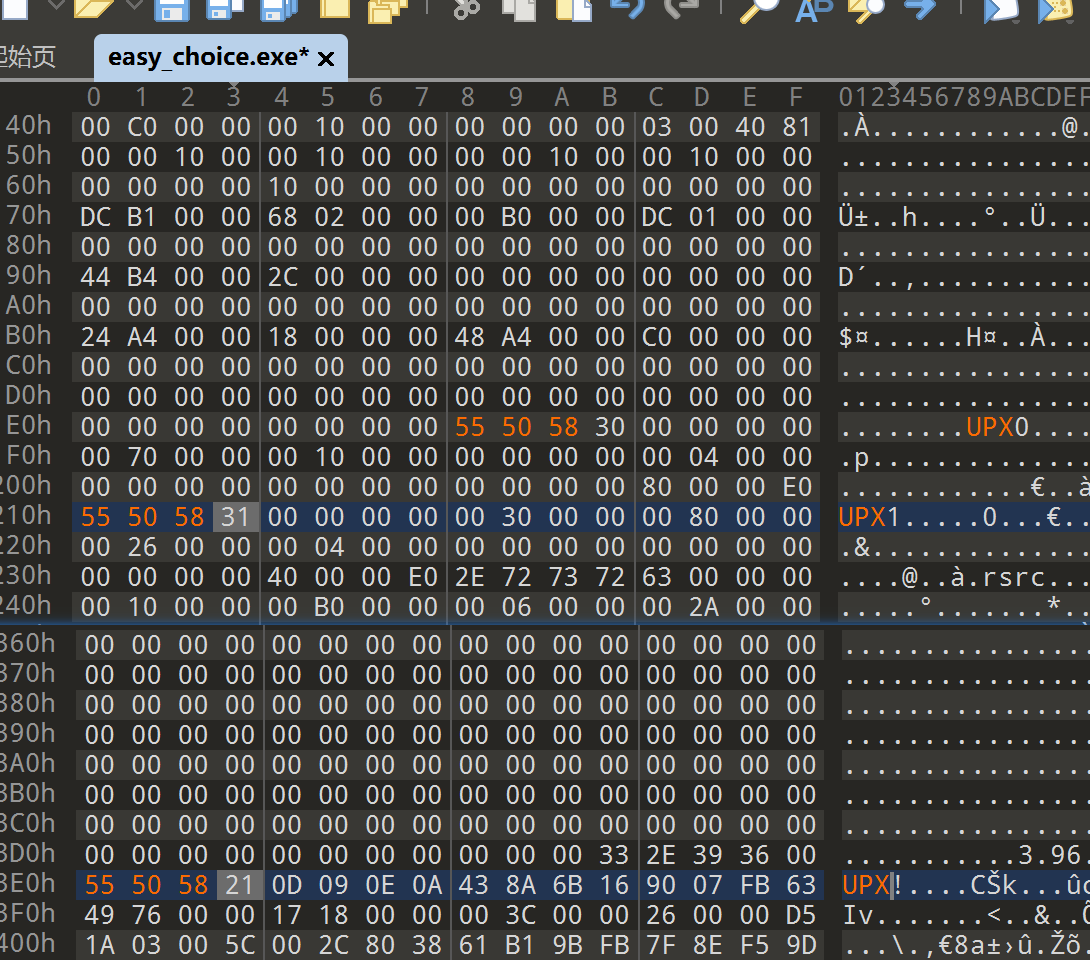
特征被修改,把它们改成正常的upx特征
改会正常特征后保存,再用工具脱壳
成功脱壳
(二)ida分析
拖入32位ida进行分析,自动定位到main函数,然后进行漫长的代码审计,在这个过程中按N键对显眼的函数、变量等修改名字,以助于后续理解
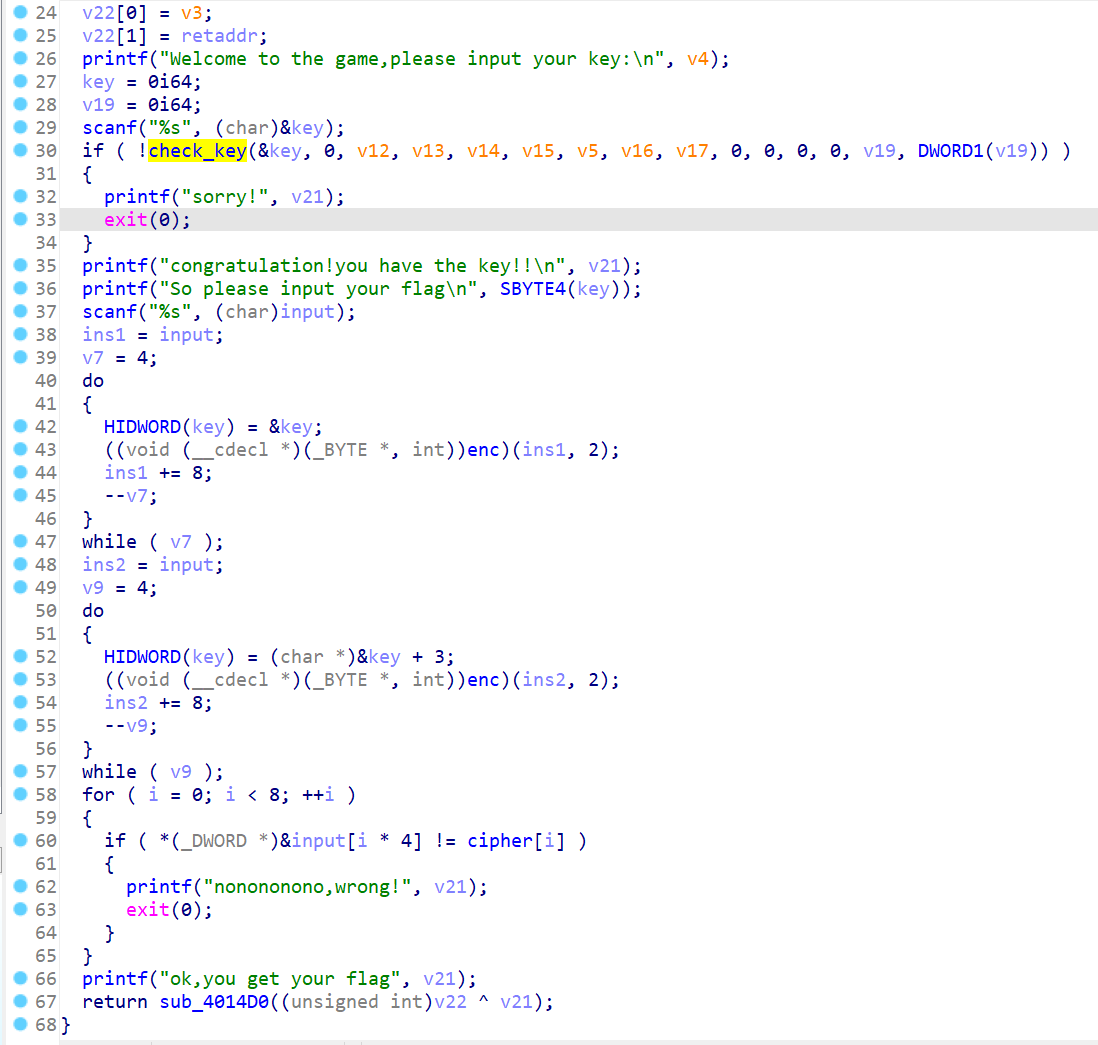
大致的逻辑是这样的:输入key->对key进行检查->输入flag->对flag进行两次加密(两个do_while循环)->检查加密后的密文是否与cipher一致
(1)check_key()分析,得到密钥
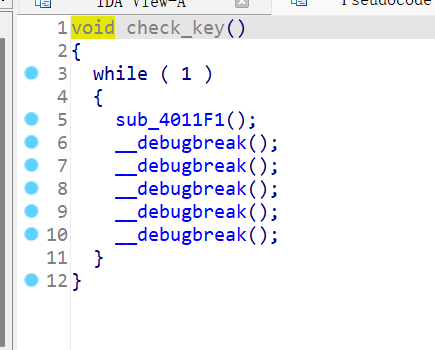
check_key()是我改的函数名,助于理解,双击函数查看代码
看到下面的代码是不是直接懵逼了……
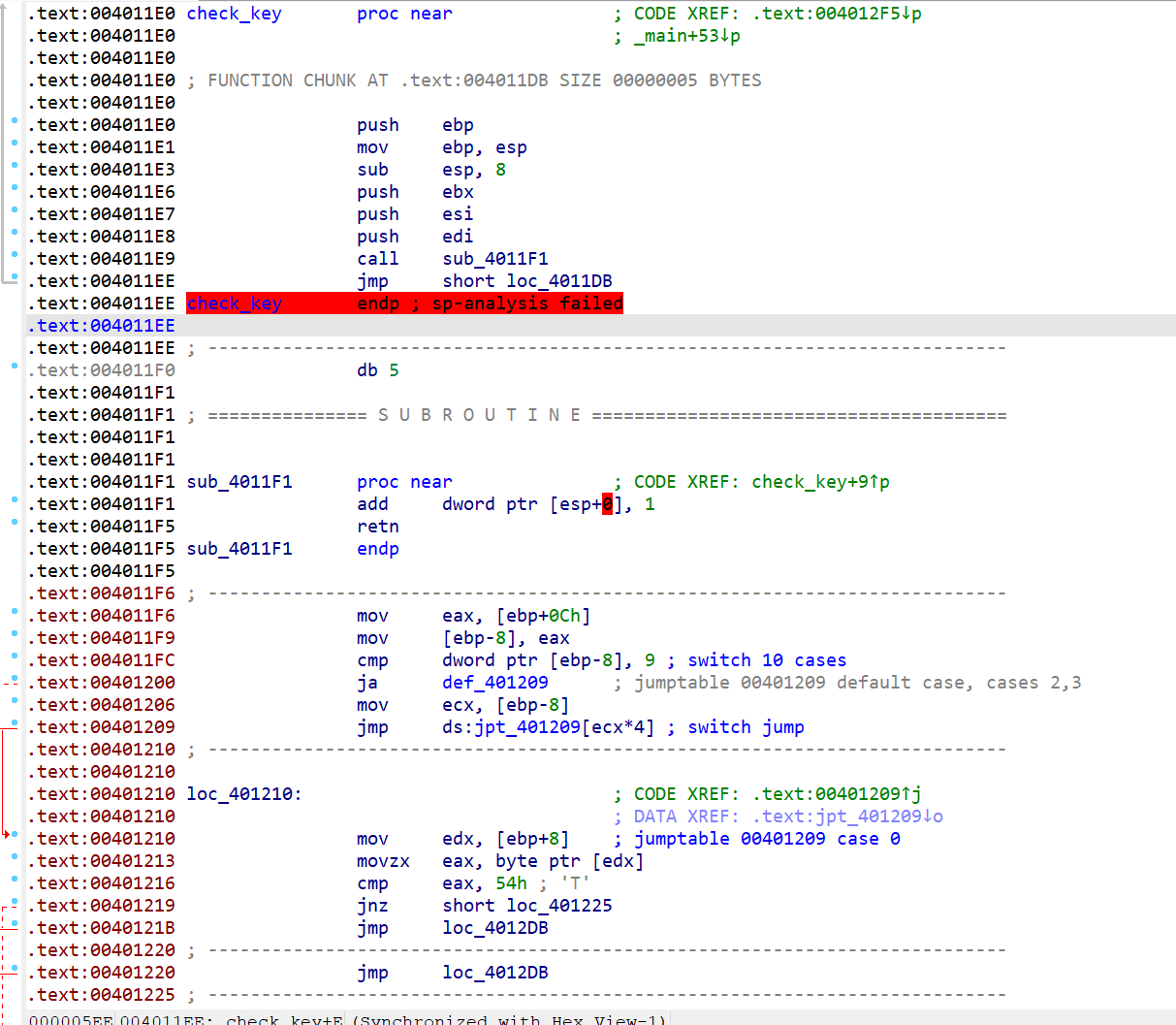
按tab键+空格看看汇编吧……丸辣,是我们最爱的花指令!如果你连花指令是什么意思都不知道,那也没必要来看这题的wp了,后面的水还深着呢……
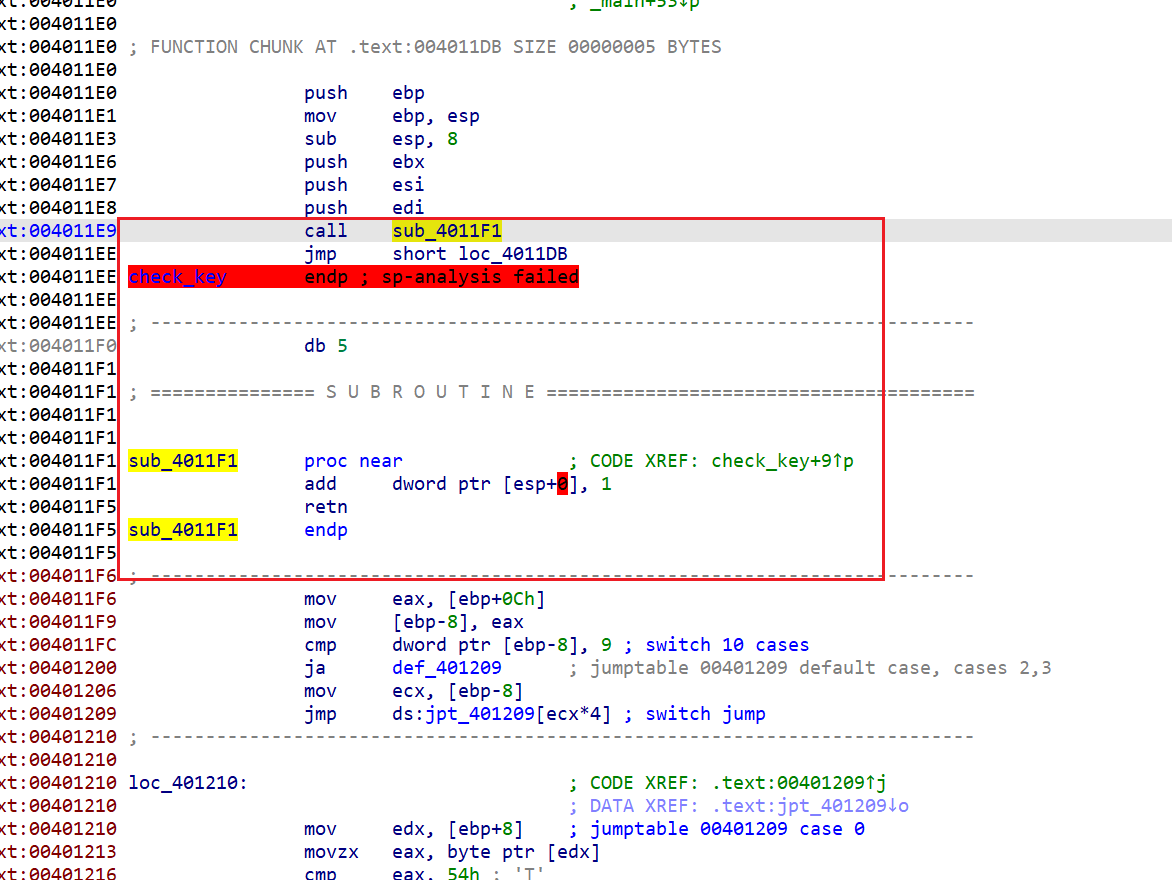
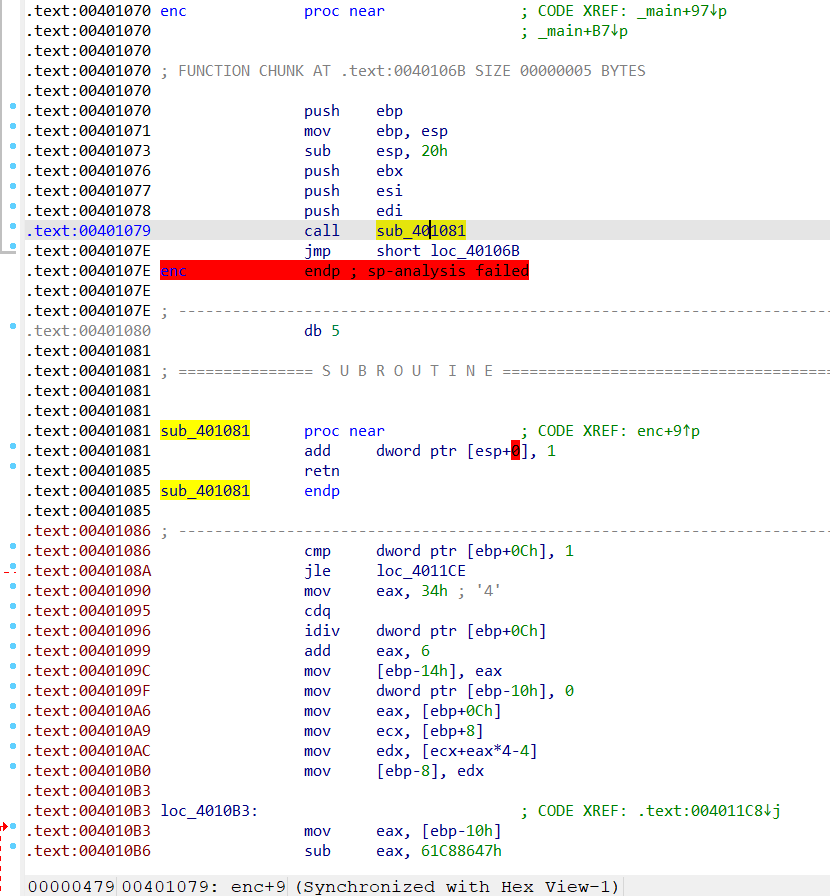
下图红框框起来的部分是本处花指令的构成,这个花指令是通过call+esp+retn的组合,扰乱ida的反汇编
花指令原理:
原文来源->花指令总结-安全客 - 安全资讯平台
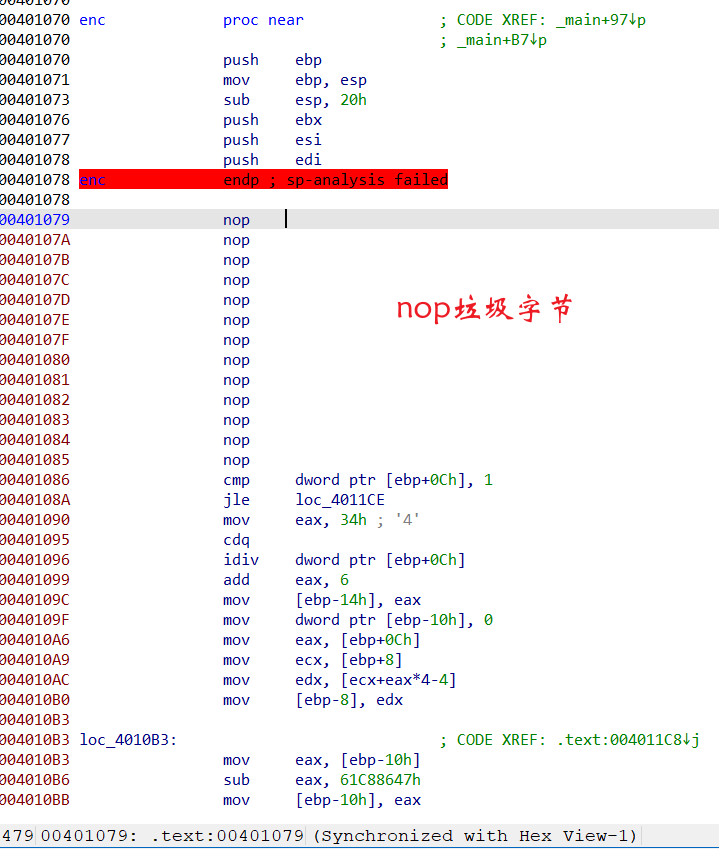
去这个花最简单粗暴的办法,全部nop,因为它们对代码正常的逻辑没有影响,可以全部视为垃圾字节(包括jmp short loc_4011DB,jmp过去的int 3只是断点指令罢了,nop掉也不影响),把垃圾字节全部nop掉,ida才能正常反汇编
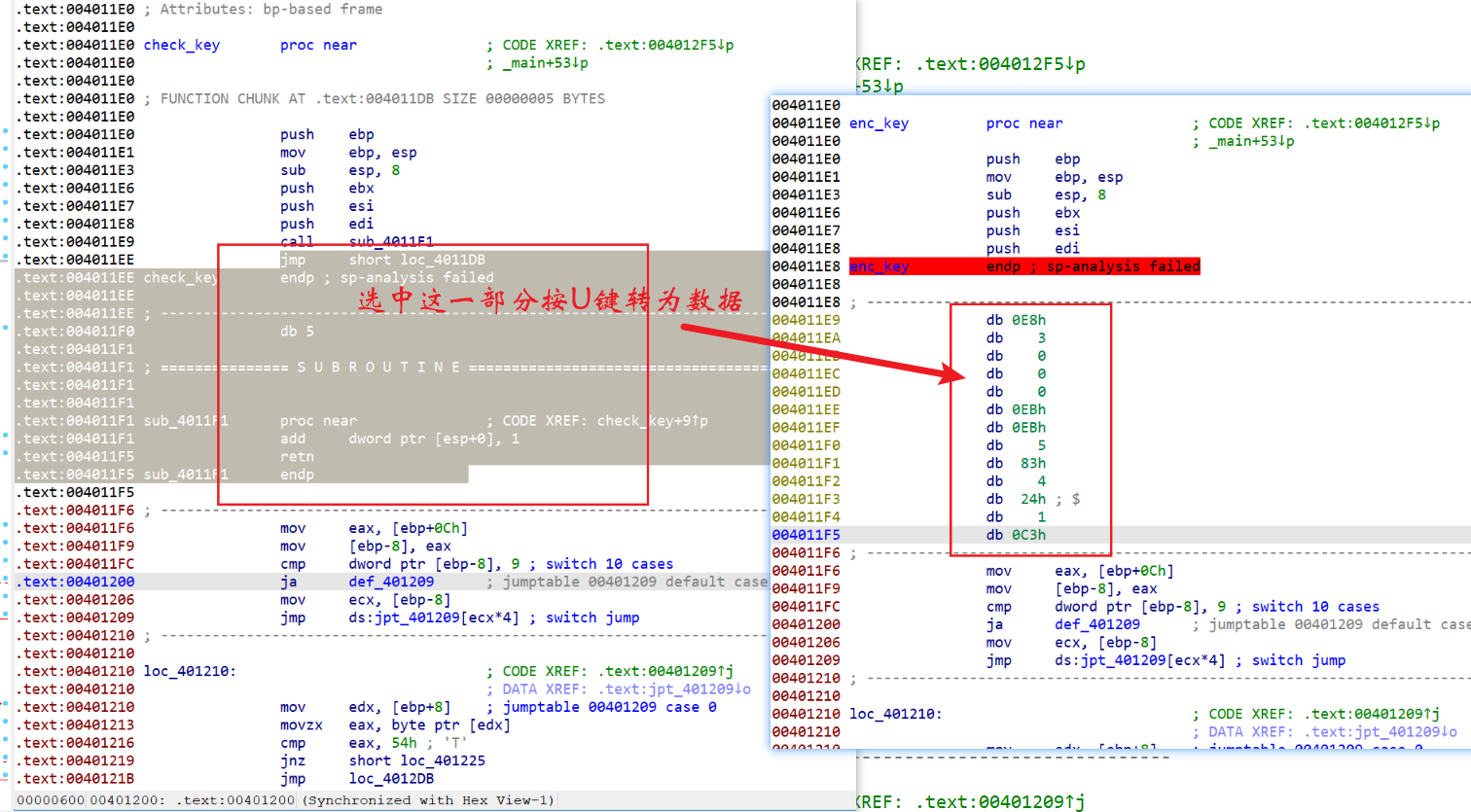
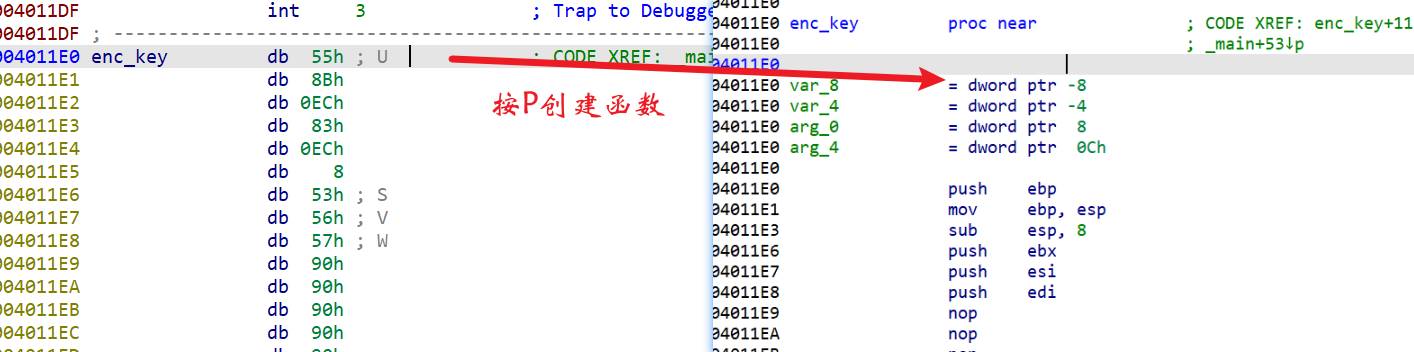
选中这部分然后按U键转为数据,这样方便我们确认要nop的范围
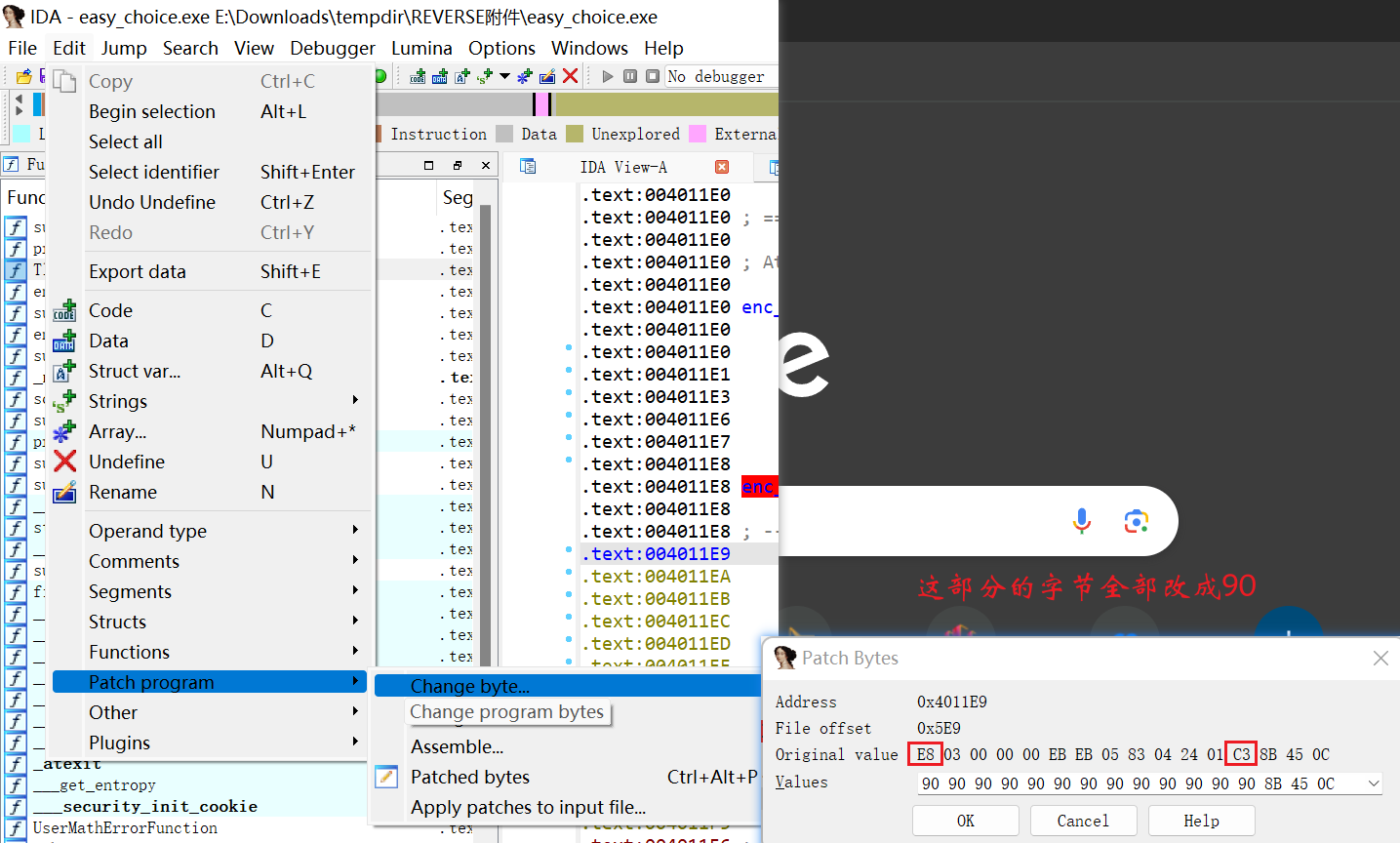
然后把这部分字节全部改成nop的字节码(0x90)
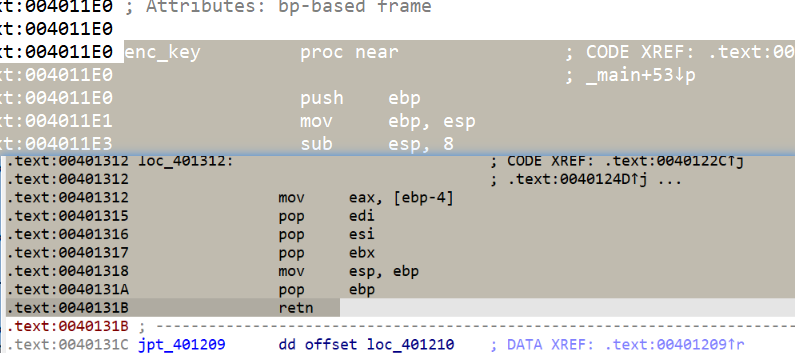
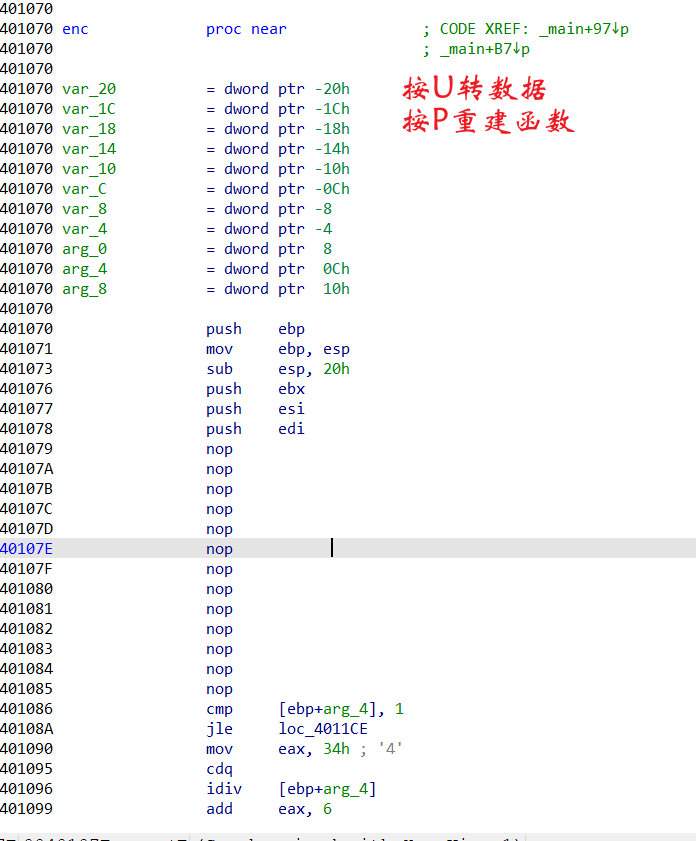
然后从函数头开始,选到下面的retn
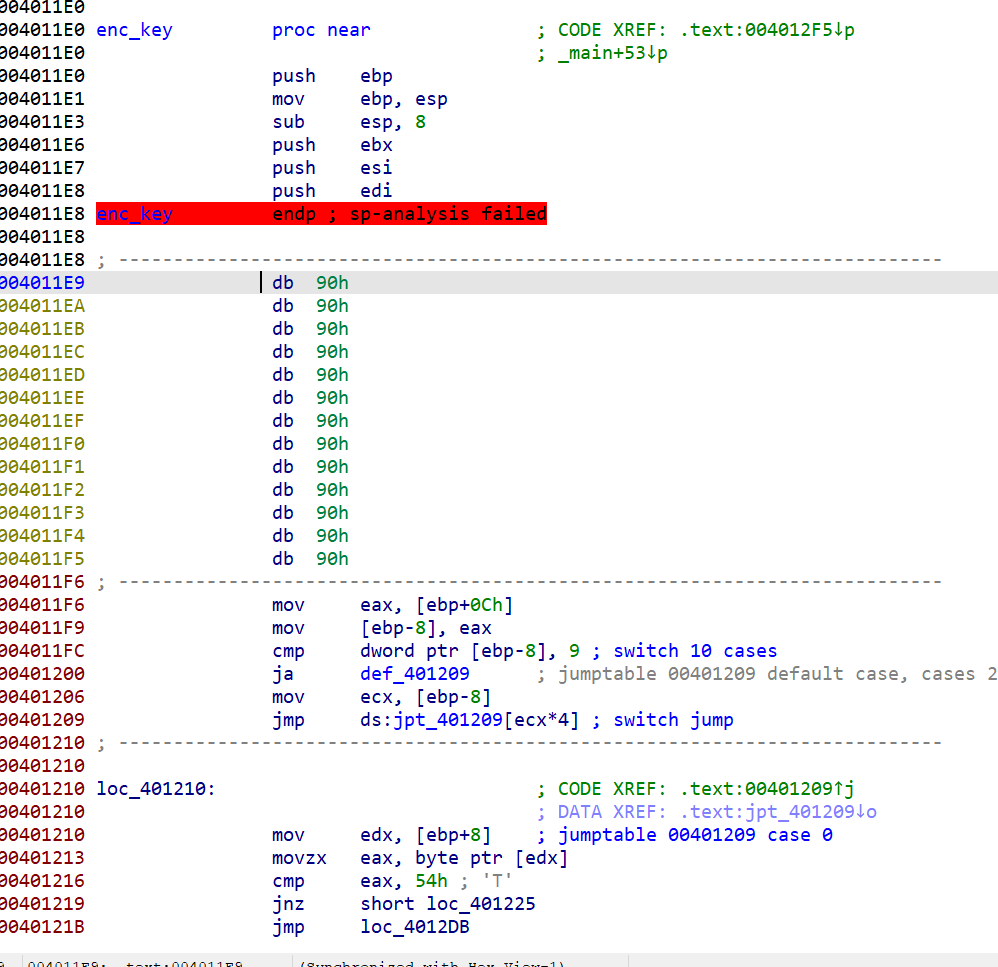
按U键转成数据后,回到函数头按P创建函数
成功去花,可以F5了!
F5看到C代码,这个逻辑其实不难,读者仔细阅读一下,这里a2刚开始是0,看传参就知道
所以把a2=0代入进去,你模拟一下就知道key是什么了,主要注意LABEL_17那里递归调用enc_key(),a2的值是在变的
注意递归调用时a1+1的意思是让按顺序访问key的每位,所以最后模拟出来的key就是正常顺序,不用去考虑要不要转大端小端之类的
模拟:
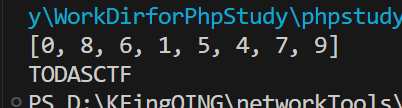
a2_arr = [] a2 = 0 # a2初始是0 for i in range(8): # 递归7次调用enc_key,a2的表达式是(8*a2+8)%11 a2_arr.append(a2) a2 = (8 * a2 + 8) % 11 # 计算下一个a2 print(a2_arr) # 从case 0-case9,给key赋的值,注意题目没有case2和case3,用0占位置,实在不理解就搓个分支赋值吧 cipher = [84, 65, 0, 0, 67, 83, 68, 84, 79, 70] for i in range(8): print(chr(cipher[a2_arr[i]]), end='') # 按递归过程中a2的值的顺序去获取每位key结果:
TODASCTF,这么标志,可以肯定是正确的key了!不确定的话就运行题目测一下能不能过check_key()
(2)enc()分析,搞清楚如何对输入进行加密
enc()也是我改的函数名,现在还不清楚它的具体加密,先在main函数里观察一下它的调用流程吧
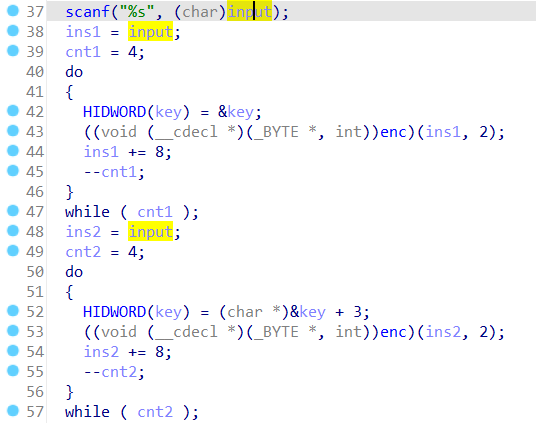
输入input之后,把input分别用ins1和ins2做了备份,然后各进行4次do...while循环,每次循环传入input和固定整数2调用enc()
重点要注意的是第二次循环时,key = &key + 3,意思很明显,第二次循环过程中用的key是向后偏移3位的
完整key: TODASCTF
第一次调用的key:TODA
第二次调用的key:ASCT
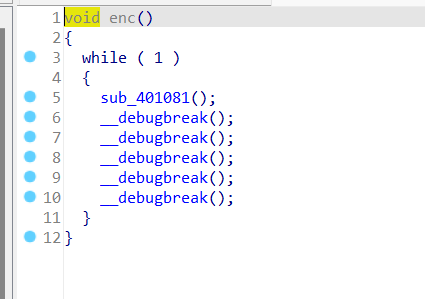
双击enc()函数查看代码……应该轻车熟路了,又是花指令
tab+空格
这题唯一良心的地方就是两个函数插入的是同一个花指令,去除方式和上面check_key()是一样的,不再赘述
又可以F5了
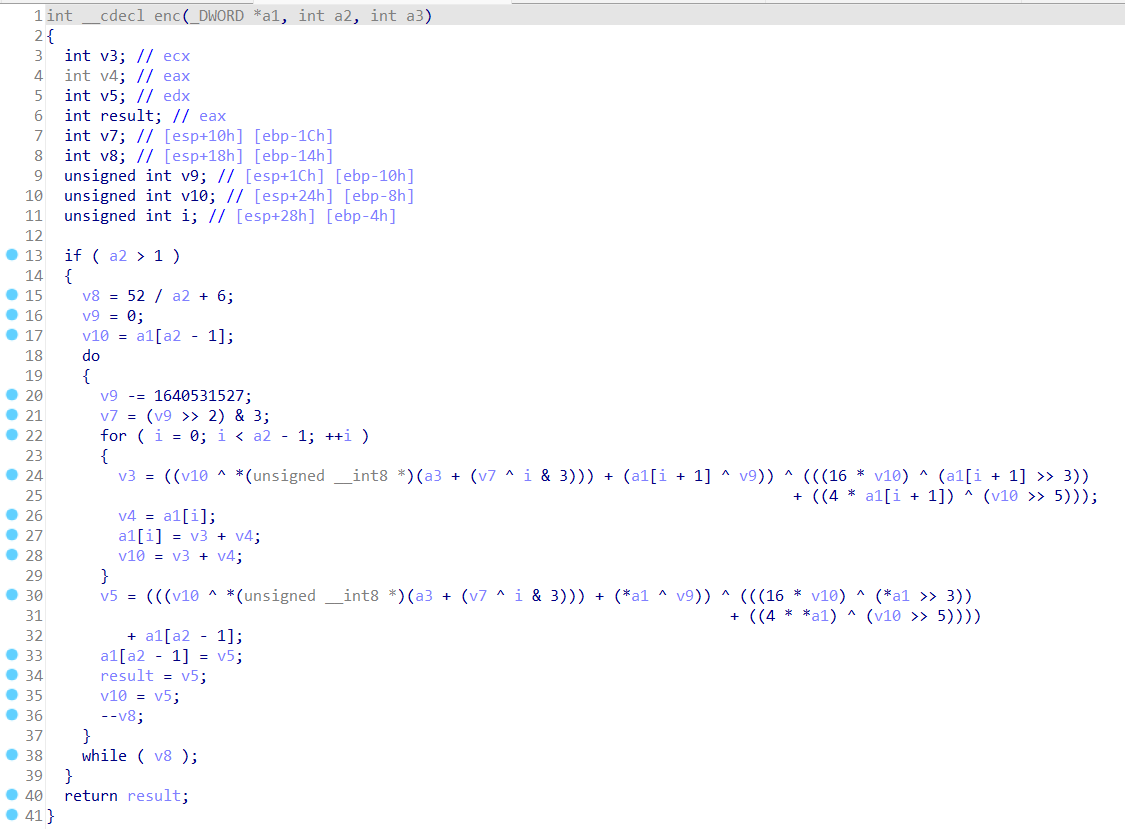
终于是见到了加密函数的庐山真面目,十分标志的xxtea(又名btea),当然如果你没学过的话,就不觉得标志了(废话)
做这种套路加密,首先一定要改好关键参数的名字,包括类型识别错的,按Y键给它改一下(比如这里的key),方便对照脚本
改的差不多就好了,有些参数不是很重要的就懒得管了,
这里要注意一点,
sum -= 0x61C88647
sum += 0x9E3779B9
这两在tea系列算法中是完全等价的,所以如果你预留的脚本里面用的delta是0x9E3779B9,不要认为和题目不一致,但注意是要sum+=0x9E3779B9
(3)总结
分析到这里终于可以写逆向脚本了
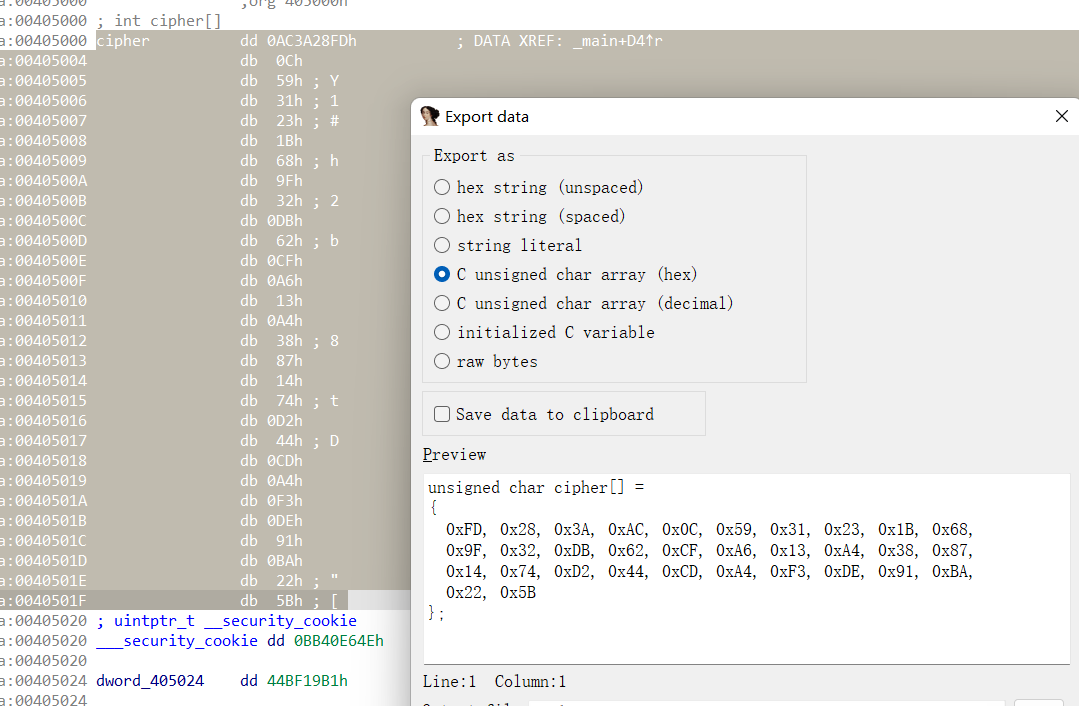
我们先把cipher提取出来
然后或是脚本,或是手搓,反正把密文处理成你脚本适配的格式,注意一下大小端序的问题
key这里还要注意,正向加密时,是
第一次调用的key:TODA
第二次调用的key:ASCT
而逆向解密时要反过来,先用"ASCT",后用"TODA"

然后做两个循环,各循环4次,每次传入v中的两个uint32_t(这里传入的-2是xxtea脚本的特性,负数是解密,正数是加密)

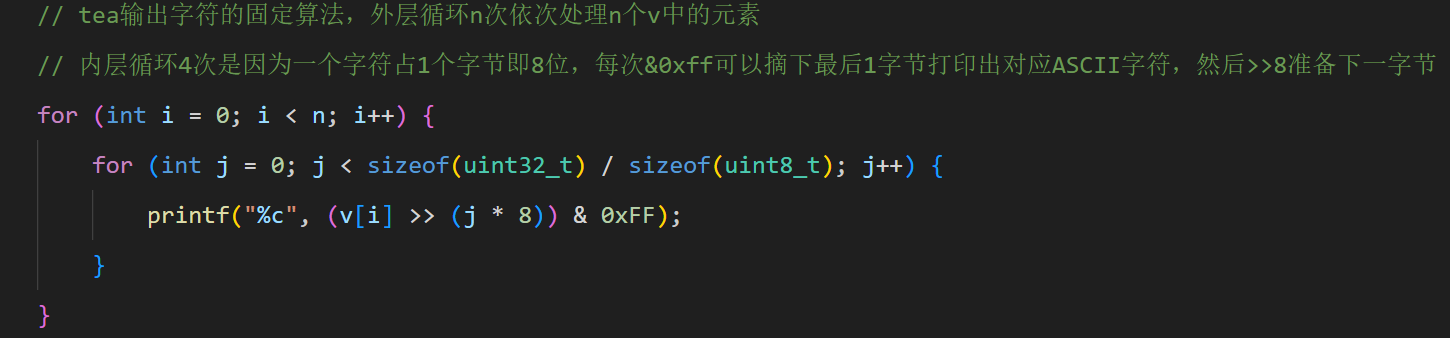
解完密后用经典算法循环&0xFF取末尾字节打印,不理解无所谓,反正是固定的输出算法
至于xxtea的解密逻辑,本题没有对其进行魔改(要是出题人还丧心病狂地魔改,这题放re第一题是真的逆了个大天),所以直接套用标准的即可
三,完整解题脚本
注:可能你觉得看wp写的脚本很简单,但这些都是一步步分析题目,不断修改和尝试出来的(比如密文密钥格式,循环设置,解密函数调用等等),所以千万不要认为看懂了wp就是学会了,一定要思考为什么是这样(比如为什么密文密钥是这个格式,为什么循环要这样设置)
exp
#include <stdint.h>
#include <stdio.h>
#define DELTA 0x9e3779b9 // 0x9e3779b9对应sum+=DELTA,而0x61C88647对应sum-=DELTA,它们是等价的
#define MX (((z >> 5 ^ y << 2) + (y >> 3 ^ z << 4)) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z)))
void btea(uint32_t* v, int n, uint32_t const key[4]) {
uint32_t y, z, sum;
unsigned p, rounds, e;
if (n > 1) /* Coding Part */
{
rounds = 6 + 52 / n;
sum = 0;
z = v[n - 1];
do {
sum += DELTA;
e = (sum >> 2) & 3;
for (p = 0; p < n - 1; p++) {
y = v[p + 1];
z = v[p] += MX;
}
y = v[0];
z = v[n - 1] += MX;
} while (--rounds);
} else if (n < -1) {
n = -n;
rounds = 6 + 52 / n;
sum = rounds * DELTA;
y = v[0];
do {
e = (sum >> 2) & 3;
for (p = n - 1; p > 0; p--) {
z = v[p - 1];
y = v[p] -= MX;
}
z = v[n - 1];
y = v[0] -= MX;
sum -= DELTA;
} while (--rounds);
}
}
int main() {
uint32_t v[8] = {
0xac3a28fd, 0x2331590c, 0x329f681b, 0xa6cf62db, 0x8738a413, 0x44d27414, 0xdef3a4cd, 0x5b22ba91,
}; // v是要加解密的数据,传入任意个32位无符号整数(一个uint32_t == 4字节)
uint32_t const k1[4] = {'A', 'S', 'C', 'T'}; // k为加密解密密钥,为4个32位无符号整数,即密钥长度为128位
uint32_t const k2[4] = {'T', 'O', 'D', 'A'};
int n = sizeof(v) / sizeof(v[0]); // n的绝对值表示v的长度,
for(int i = 0; i < 4; i++){
btea(v + 2 * i, -2, k1);
}
for(int i = 0; i < 4; i++){
btea(v + 2 * i, -2, k2);
}
// tea输出字符的固定算法,外层循环n次依次处理n个v中的元素
// 内层循环4次是因为一个字符占1个字节即8位,每次&0xff可以摘下最后1字节打印出对应ASCII字符,然后>>8准备下一字节
for (int i = 0; i < n; i++) {
for (int j = 0; j < sizeof(uint32_t) / sizeof(uint8_t); j++) {
printf("%c", (v[i] >> (j * 8)) & 0xFF);
}
}
return 0;
}