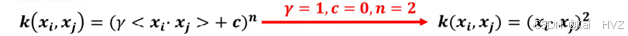文章目录
什么是支持向量机?
- 支持向量机(Support Vector Machine,SVM)是一种监督式学习的分类算法,也可用于回归分析。它的主要目标是在特征空间中找到一个最优的超平面,从而将不同类别的数据点尽可能分开。这个超平面被定义为能够使两类数据之间的间隔(Margin)最大的平面。
基本原理
- 线性可分情况
-
假设有两类数据点,分别标记为正类和负类。在二维空间中,这些数据点可以用平面直角坐标系中的点来表示。如果这些数据是线性可分的,那么可以找到一条直线(在高维空间中是超平面)将这两类数据分开。
-
-
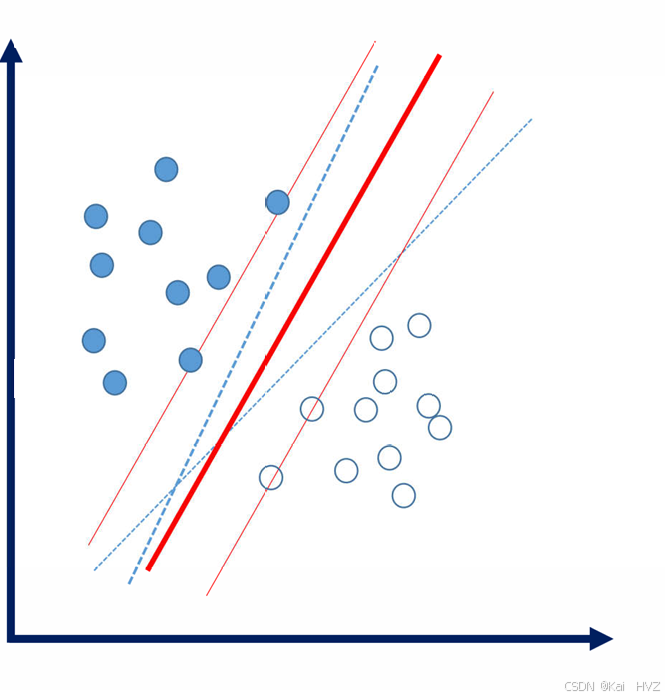
支持向量机在寻找这个分离超平面时,不仅要找到能分开两类数据的平面,还要使这个平面到两类数据中最近的数据点的距离最大。这些最近的数据点就被称为支持向量。
-
- 非线性可分情况
-
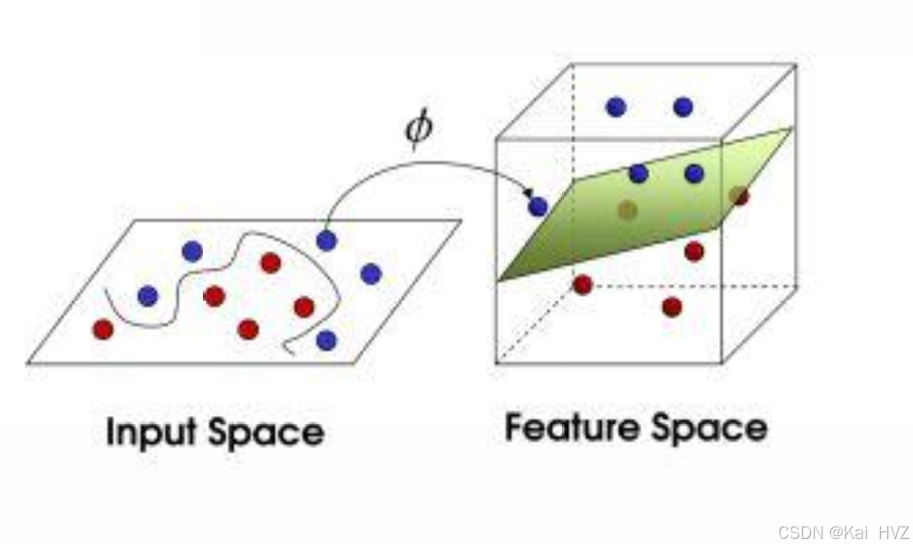
当数据在原始空间中不是线性可分的时候,支持向量机通过使用核函数(Kernel Function)将原始数据映射到一个高维空间,使得在高维空间中数据变得线性可分。
-
-
例如,在二维平面上有一个圆形分布的数据,正类在圆内,负类在圆外,这在二维空间中无法用直线分开。但是通过核函数将其映射到三维空间后,就可能找到一个平面将它们分开。常用的核函数有线性核、多项式核、高斯核(径向基函数核)等。
-
数学模型
- 目标函数
- 拉格朗日乘子法求解
支持向量机模型
模型参数
重要的参数有:C、kernel、degree、gamma。
- C:
- 惩罚因子【浮点数,默认为1.】【软间隔】
- (1)C越大,对误分类的惩罚增大,希望松弛变量接近0,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱;
- (2)C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
- ->>建议通过交叉验证来选择
- kernel:
- 核函数【默认rbf(径向基核函数|高斯核函数)】
- 可以选择线性(linear)、多项式(poly)、sigmoid
- ->>多数情况下选择rbf
- degree:
- 【整型,默认3维】
- 多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
- ->>按默认【选择rbf之后,此参数不起作用】
- 指上面式子中的n
- gamma:
- ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’。
- (1)如果gamma是’auto’,那么实际系数是1 / n_features,也就是数据如果有10个特征,那么gamma值维0.1。(sklearn0.21版本)
- (2)在sklearn0.22版本中,默认为’scale’,此时gamma=1 / (n_features*X.var())#X.var()数据集所有值的方差。
- <1>gamma越大,过拟合风险越高
- <2> gamma越小,过拟合风险越低
- ->>建议通过交叉验证来选择
- coef0:
- 核函数中的独立项。多项式的偏置项。它只在’poly’和’sigmoid’中很重要。
- probability :
- 是否启用概率估计。允许在模型训练完成后,使用predict_proba方法来预测每个类别的概率,而不是仅仅给出类别的预测结果。必须在调用fit之前启用它,并且会减慢该方法的速度。默认为False
- ->>按默认即可【选择rbf之后,不起作用】
- cache_size:
- 核函数cache缓存大小,默认为200MB
- ->>不用调整
- class_weight:
- 类别的权重,字典形式传递。默认’balanced’
- ->>按默认设置
属性信息
- support_vectors_ 【支持向量】
- 以数组的形式储存
- n_support_ 【每个类别支持向量的个数】
- int类型
- coef_ 【参数w】
- 数组的形式储存
- intercept_ 【偏置项参数b】
- 数组的形式储存
支持向量机实例(1)
实例要求:从鸢尾花数据中,对鸢尾花进行分类。
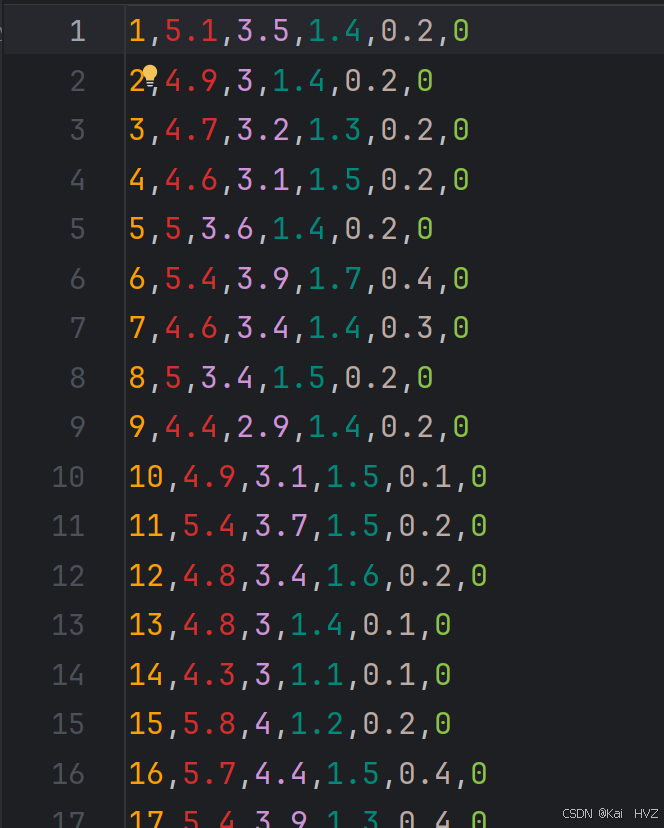
数据内容:数据中共有100条样本数据,6列,其中第一列为编号数据,最后一列为标签数据,其余4列为特征数据。且前50行数据的标签为0,后50行数据标签为1.
数据:通过网盘分享的文件:iris.csv
链接: https://pan.baidu.com/s/1ssc_VSVSUbkzz2-SOipV9w 提取码: jq54
实例步骤
- 读取数据
- 可视化原始数据
- 使用支持向量机训练
- 可视化支持向量机结果
- 绘制分割线和间隔边界、支持向量
读取数据
import pandas as pd
data = pd.read_csv(r'D:\where-python\python-venv\ji_qi_xue_xi_demo\朴素贝叶斯\iris.csv', header=None)
# header=None 为没有表头
可视化原始数据
import matplotlib.pyplot as plt
# 选取数据的前 50 行
data1 = data.iloc[:50, :]
# 选取数据的 50 行之后的数据
data2 = data.iloc[50:, :]
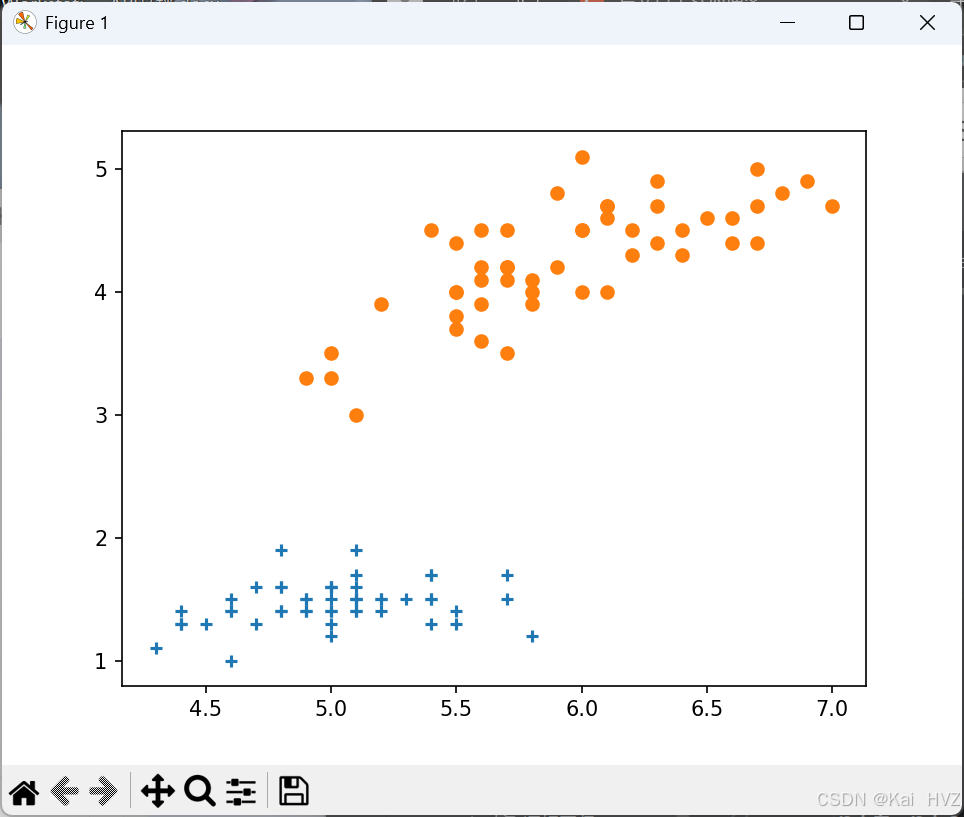
# 原始数据是四维,无法展示,选择两个维度进行展示,使用 scatter 函数绘制散点图
# 以数据 1 的第 1 列和第 3 列作为 x 和 y 轴,标记为 + 号
plt.scatter(data1[1], data1[3], marker='+')
# 以数据 2 的第 1 列和第 3 列作为 x 和 y 轴,标记为 o 号
plt.scatter(data2[1], data2[3], marker='o')
# 显示绘制的散点图
plt.show()
使用支持向量机训练
from sklearn.svm import SVC
# 选取数据的第 1 列和第 3 列作为特征 x
x = data.iloc[:, [1, 3]]
# 选取数据的最后一列作为标签 y
y = data.iloc[:, -1]
# 创建 SVC 分类器,使用线性核,C 为无穷大,随机种子为 0
svm = SVC(kernel='linear', C=float('inf'), random_state=0)
# 用选取的特征和标签训练 SVC 分类器
svm.fit(x, y)
可视化支持向量机结果
# 获取训练好的分类器的系数
w = svm.coef_[0]
# 获取截距
b = svm.intercept_[0]
import numpy as np
# 生成 0 到 7 之间的 300 个等间距的点
x1 = np.linspace(0, 7, 300)
# 计算分割超平面的直线方程,w[0] * x1 + w[1] * x2 + b = 0,解出 x2
x2 = -(w[0] * x1 + b) / w[1]
# 计算间隔边界直线方程,w[0] * x1 + w[1] * x2 + b = 1,解出 x2
x3 = (1 - (w[0] * x1 + b)) / w[1]
# 计算间隔边界直线方程,w[0] * x1 + w[1] * x2 + b = -1,解出 x2
x4 = (-1 - (w[0] * x1 + b)) / w[1]
# 绘制分割超平面,线宽为 2,颜色为红色
plt.plot(x1, x2, linewidth=2, color='r')
# 绘制间隔边界,线宽为 1,颜色为红色,线条样式为虚线
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--')
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--')
# 设置 x 轴范围
plt.xlim(4, 7)
# 设置 y 轴范围
plt.ylim(0, 5)
# 获取支持向量
vets = svm.support_vectors_
# 绘制支持向量,颜色为蓝色,标记为 x
plt.scatter(vets[:, 0], vets[:, 1], c='b', marker='x')
# 显示最终的图像
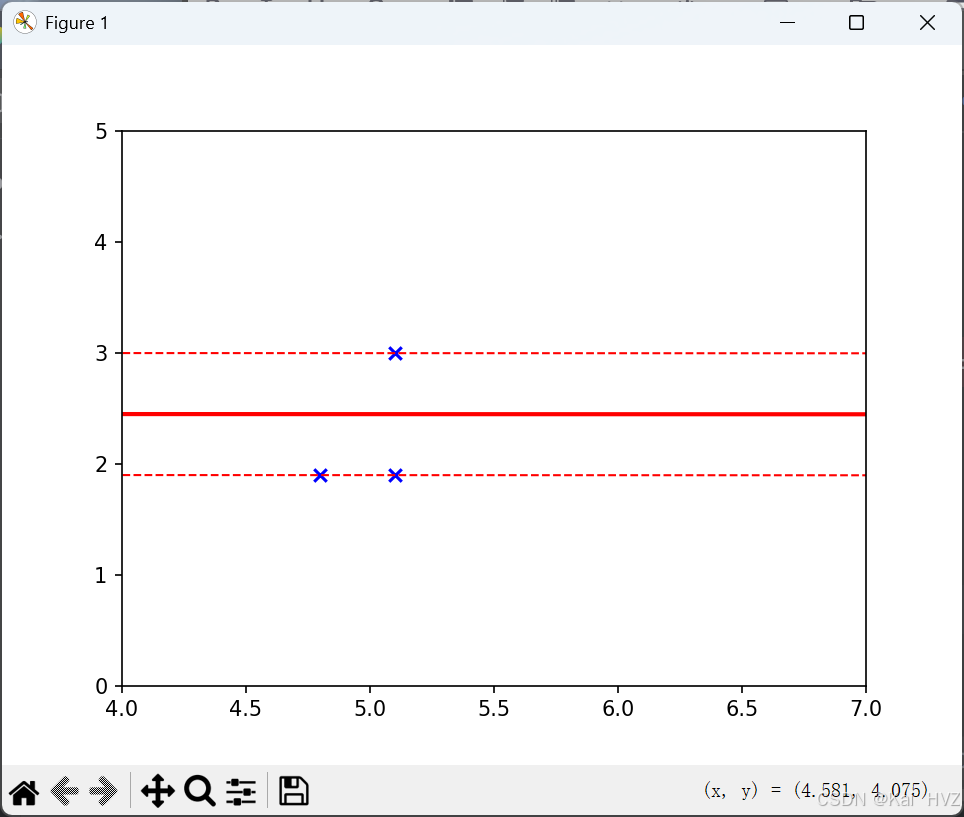
plt.show()
本次实例可看出在二维中支持向量机的情况,绘制分割线和支持向量的分布。
完整代码
import pandas as pd
# 读取 csv 文件,文件路径需要注意转义字符,可使用原始字符串
data = pd.read_csv(r'D:\where-python\python-venv\ji_qi_xue_xi_demo\朴素贝叶斯\iris.csv', header=None)
import matplotlib.pyplot as plt
# 选取数据的前 50 行
data1 = data.iloc[:50, :]
# 选取数据的 50 行之后的数据
data2 = data.iloc[50:, :]
# 原始数据是四维,无法展示,选择两个维度进行展示,使用 scatter 函数绘制散点图
# 以数据 1 的第 1 列和第 3 列作为 x 和 y 轴,标记为 + 号
plt.scatter(data1[1], data1[3], marker='+')
# 以数据 2 的第 1 列和第 3 列作为 x 和 y 轴,标记为 o 号
plt.scatter(data2[1], data2[3], marker='o')
# 显示绘制的散点图
plt.show()
from sklearn.svm import SVC
# 选取数据的第 1 列和第 3 列作为特征 x
x = data.iloc[:, [1, 3]]
# 选取数据的最后一列作为标签 y
y = data.iloc[:, -1]
# 创建 SVC 分类器,使用线性核,C 为无穷大,随机种子为 0
svm = SVC(kernel='linear', C=float('inf'), random_state=0)
# 用选取的特征和标签训练 SVC 分类器
svm.fit(x, y)
# 获取训练好的分类器的系数
w = svm.coef_[0]
# 获取截距
b = svm.intercept_[0]
import numpy as np
# 生成 0 到 7 之间的 300 个等间距的点
x1 = np.linspace(0, 7, 300)
# 计算分割超平面的直线方程,w[0] * x1 + w[1] * x2 + b = 0,解出 x2
x2 = -(w[0] * x1 + b) / w[1]
# 计算间隔边界直线方程,w[0] * x1 + w[1] * x2 + b = 1,解出 x2
x3 = (1 - (w[0] * x1 + b)) / w[1]
# 计算间隔边界直线方程,w[0] * x1 + w[1] * x2 + b = -1,解出 x2
x4 = (-1 - (w[0] * x1 + b)) / w[1]
# 绘制分割超平面,线宽为 2,颜色为红色
plt.plot(x1, x2, linewidth=2, color='r')
# 绘制间隔边界,线宽为 1,颜色为红色,线条样式为虚线
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--')
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--')
# 设置 x 轴范围
plt.xlim(4, 7)
# 设置 y 轴范围
plt.ylim(0, 5)
# 获取支持向量
vets = svm.support_vectors_
# 绘制支持向量,颜色为蓝色,标记为 x
plt.scatter(vets[:, 0], vets[:, 1], c='b', marker='x')
# 显示最终的图像
plt.show()
支持向量机实例(2)
对手写体图片进行识别。
共有2000个手写体数据,上面是一张已经经过一些初步处理过的图片,其中含有0~9的手写数字,且每一个数字都是5行,100列,共有5000个数字。
本次通过对这张分辨率为20001000的图片进行切分。将其划分成独立的数字,每个数字大小为2020像素,共计5000个。
实例步骤
- 导入数据
- 处理数据
- 切分划分数据
- 创建SVM模型
- 训练数据
- 测试数据
- 得到分类报告及准确率
导入数据
import numpy as np
import cv2
# 读取图像文件 shu_zi.png
img = cv2.imread('shu_zi.png')
处理数据
# 将图像从 BGR 颜色空间转换为灰度空间
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 将灰度图像划分为 50 行,每行再划分为 100 列,生成一个二维列表 cells
cells = [np.hsplit(row, 100) for row in np.vsplit(gray, 50)]
# 将二维列表转换为 numpy 数组
x = np.array(cells)
# 将数组重塑为 (-1, 400) 的形状,并将数据类型转换为 float32
x = x.reshape(-1, 400).astype(np.float32)
# 创建一个从 0 到 9 的数组
k = np.arange(10)
# 将数组 k 中的元素重复 500 次,生成标签数组 y
y = np.repeat(k, 500)
切分划分数据
from sklearn.model_selection import train_test_split
# 将数据 x 和标签 y 划分为训练集和测试集,测试集占 20%,设置随机种子为 0
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(x, y, test_size=0.2, random_state=0)
创建SVM模型
from sklearn.svm import SVC
# 创建 SVC 分类器,使用径向基核函数(rbf),C 为无穷大,随机种子为 0
svm = SVC(kernel='rbf', C=float('inf'), random_state=0)
训练数据
# 使用训练集数据 x_train_w 和标签 y_train_w 训练 SVC 分类器
svm.fit(x_train_w, y_train_w)
测试数据
自测
from sklearn import metrics
# 使用训练好的分类器对训练集数据进行预测
train_pred = svm.predict(x_train_w)
测试集测试
# 使用训练好的分类器对测试集数据进行预测
test_pred = svm.predict(x_test_w)
得到分类报告及准确率
# 输出训练集的分类性能报告,包括精确率、召回率、F1 分数等指标
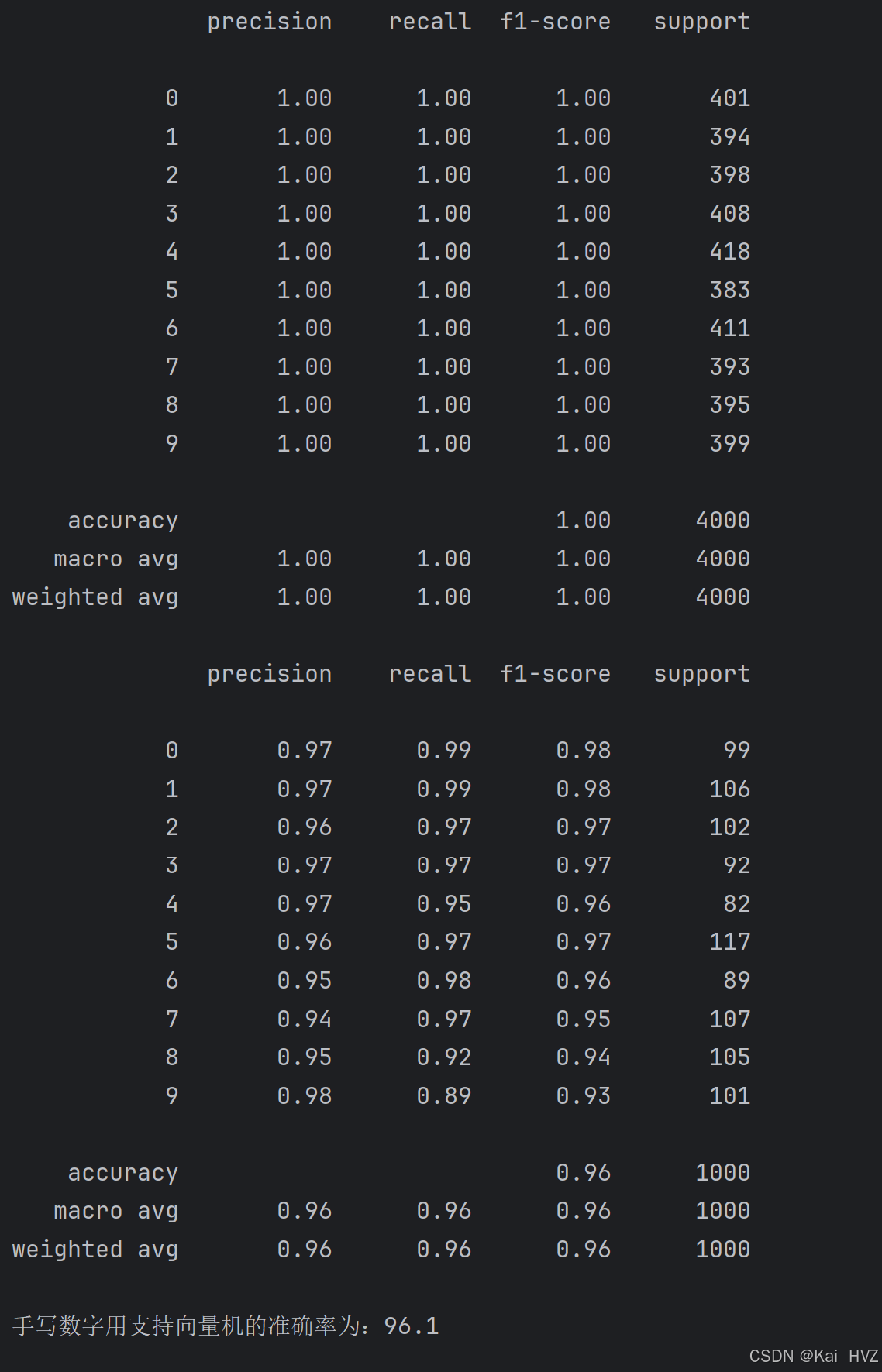
print(metrics.classification_report(y_train_w, train_pred))
# 输出测试集的分类性能报告
print(metrics.classification_report(y_test_w, test_pred))
# 计算分类器在测试集上的准确率
m = svm.score(x_test_w, y_test_w)
# 打印手写数字用支持向量机的准确率
print(f'手写数字用支持向量机的准确率为:{m}')
完整代码
import numpy as np
import cv2
# 导入 cv2 库用于图像处理,导入 numpy 库用于数据处理
# 读取图像文件 shu_zi.png
img = cv2.imread('shu_zi.png')
# 将读取的图像从 BGR 颜色空间转换为灰度颜色空间
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 使用 np.vsplit 将灰度图像分割成 50 行,对每一行使用 np.hsplit 分割成 100 列
# 将结果存储在 cells 列表中,列表中的每个元素是分割后的图像块
cells = [np.hsplit(row, 100) for row in np.vsplit(gray, 50)]
# 将 cells 列表转换为 numpy 数组
x = np.array(cells)
# 将数组重塑为 (-1, 400) 的形状,并将数据类型转换为 float32
# 目的是将数据处理为适合机器学习算法的格式
x = x.reshape(-1, 400).astype(np.float32)
# 创建一个包含 0 到 9 的数组
k = np.arange(10)
# 将数组 k 中的元素重复 500 次,作为标签数据
y = np.repeat(k, 500)
from sklearn.model_selection import train_test_split
# 将数据 x 和标签 y 按照 80:20 的比例划分为训练集和测试集
# random_state=0 保证每次运行代码划分结果相同
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(x, y, test_size=0.2, random_state=0)
from sklearn.svm import SVC
# 创建 SVC 分类器,使用径向基核函数(rbf),C 为无穷大,随机种子为 0
svm = SVC(kernel='rbf', C=float('inf'), random_state=0)
# 使用训练集数据 x_train_w 和标签 y_train_w 训练 SVC 分类器
svm.fit(x_train_w, y_train_w)
from sklearn import metrics
# 使用训练好的分类器对训练集数据进行预测
train_pred = svm.predict(x_train_w)
# 输出训练集的分类性能报告,包括精确率、召回率、F1 分数等指标
print(metrics.classification_report(y_train_w, train_pred))
# 使用训练好的分类器对测试集数据进行预测
test_pred = svm.predict(x_test_w)
# 输出测试集的分类性能报告
print(metrics.classification_report(y_test_w, test_pred))
# 计算分类器在测试集上的准确率
m = svm.score(x_test_w, y_test_w)
# 打印手写数字用支持向量机的准确率
print(f'手写数字用支持向量机的准确率为:{m}')
与KNN算法准确率做对比
KNN完整代码
import numpy as np
import cv2
img =cv2.imread('shu_zi.png')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
cells = [np.hsplit(row,100) for row in np.vsplit(gray,50)]
x =np.array(cells)
train = x[:,:50]
test =x[:,50:100]
# 将数据构造为符合KNN的输入,将每个数字的尺寸由20*20调整为1*400
train_new = train.reshape(-1,400).astype(np.float32)
test_new = test.reshape(-1,400).astype(np.float32)
# 分配标签:分别为训练数据、测试数据分配标签
k = np.arange(10)
labels = np.repeat(k,250)
train_labels = labels[:,np.newaxis] # np.newaxis是numpy库中一个特殊对象用于增加一个新的维度
test_labels = np.repeat(k,250)[:,np.newaxis]
# # # 构建+训练
knn =cv2.ml.KNearest_create() # 通过cv2创建一个knn模型
knn.train(train_new,cv2.ml.ROW_SAMPLE,train_labels)
ret,result,neighbours,dist=knn.findNearest(test_new,k=3)
# ret,result,neighbours,dist=knn.findNearest(a3,k=3)
# # ret:表示查找操作是否成功
# # result:浮点数数组,表示测试样本的预测标签
# # neighbours:这是一个整数数组,表示与测试样本最近的k个索引。
# # dist:这是一个浮点数组,表示测试样本与每一个最近邻居之间的距离。
matches = result==test_labels
correct = np.count_nonzero(matches)
accuracy = correct*100.0/result.size
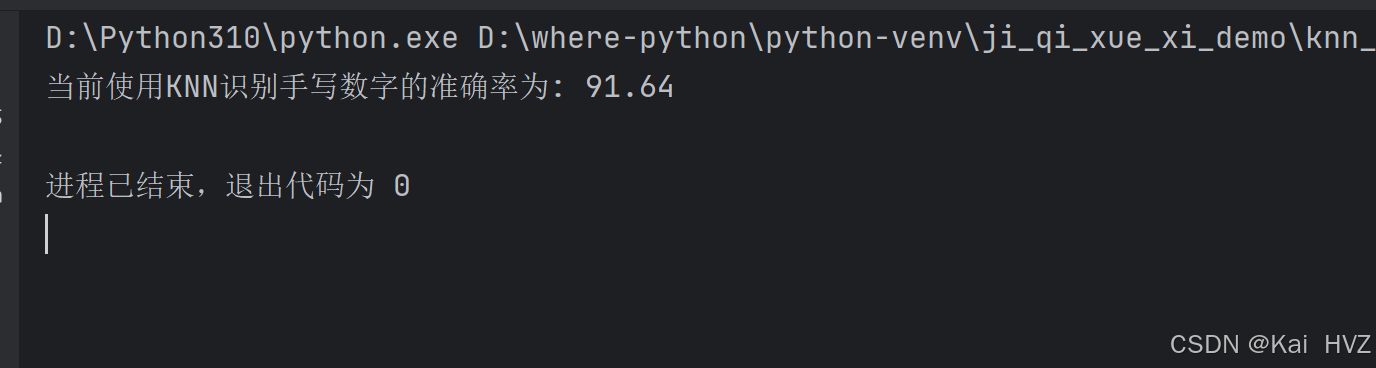
print("当前使用KNN识别手写数字的准确率为:",accuracy)
从支持向量机算法和KNN算法对比,可看到支持向量机的准确率更高。