✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
⛄ 内容介绍
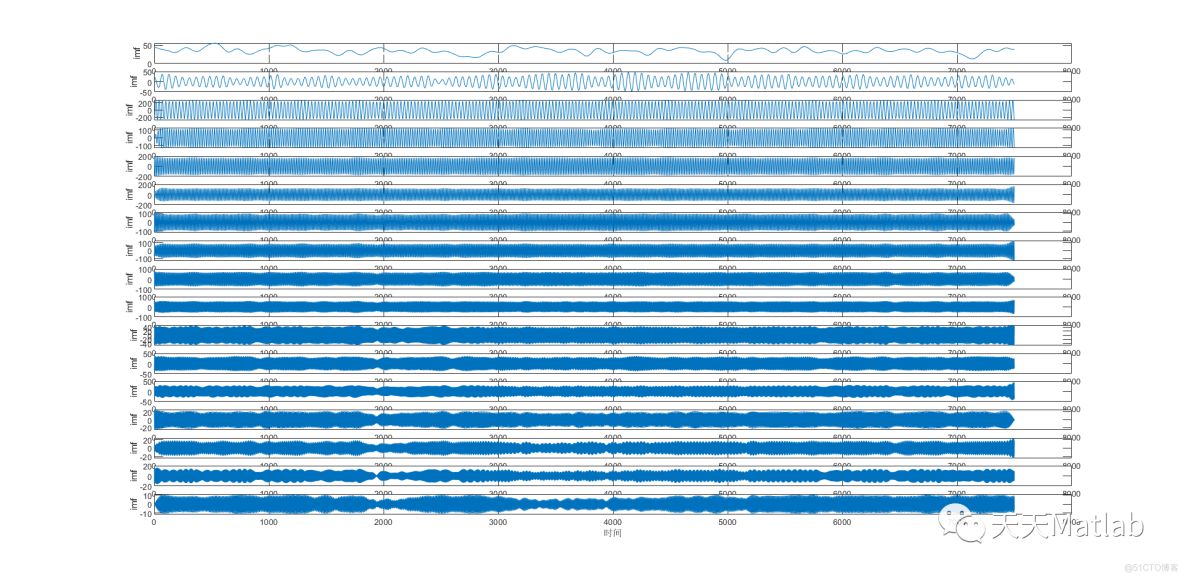
逐次变分模态分解(Sequential Variational Mode Decomposition,简称SVMD)是一种用于信号处理和数据分析的方法。它可以将复杂的信号分解为一系列模态函数,每个模态函数代表了信号中的一个特定频率成分。SVMD的主要目标是提取信号中的不同频率成分,并将其重构为原始信号。
SVMD的基本原理是通过变分模态分解的方式将信号分解为多个模态函数。在每个迭代步骤中,SVMD通过最小化信号与模态函数之间的差异来更新模态函数。这个过程会不断重复,直到收敛为止。最终得到的模态函数可以用于重构原始信号。
SVMD的另一个关键特点是逐次分解。在每个迭代步骤中,SVMD会从信号中提取出一个主要的频率成分,并将其从信号中剔除。这样,每个迭代步骤都会提取出信号中的一个频率成分,直到所有的频率成分都被提取完毕。这种逐次分解的方式可以更好地捕捉到信号中的不同频率成分。
SVMD在信号处理和数据分析中有广泛的应用。它可以用于去噪、特征提取、频谱分析等多个领域。通过将信号分解为模态函数,SVMD可以更好地理解和描述信号的频率特征。这对于信号处理和数据分析来说是非常重要的。
SVMD的数据重构是将分解得到的模态函数重新组合成原始信号的过程。通过将每个模态函数加权相加,可以得到重构后的信号。这个过程可以用于还原原始信号的频率特征,并且可以根据需要进行进一步的分析和处理。
总之,逐次变分模态分解是一种用于信号处理和数据分析的有效方法。它可以将复杂的信号分解为多个模态函数,并且可以通过数据重构将其重新组合成原始信号。SVMD的应用领域广泛,对于理解和描述信号的频率特征非常有帮助。通过深入研究和应用SVMD,我们可以更好地处理和分析各种类型的信号和数据。
⛄ 核心代码
%% This is a script to test the SVMD method
close all
clear
clc
%% Example 1 (ECG signal)
load('ECG.mat');
signal=(val (1,:));
%----------------- Initialization
maxAlpha=20000; %compactness of mode
tau=0;%time-step of the dual ascent
tol=1e-6; %tolerance of convergence criterion;
stopc=4;%the type of stopping criteria
fs=125; % sampling frequency
T = length(signal);% time domain (t -->> 0 to T)
t = (1:T)/T;
omega_freqs = t-0.5-1/T;%discretization of spectral domain
f_hat=fftshift(fft(signal));
%-------------- SVMD function
[u,uhat]=svmd(signal,maxAlpha,tau,tol,stopc);
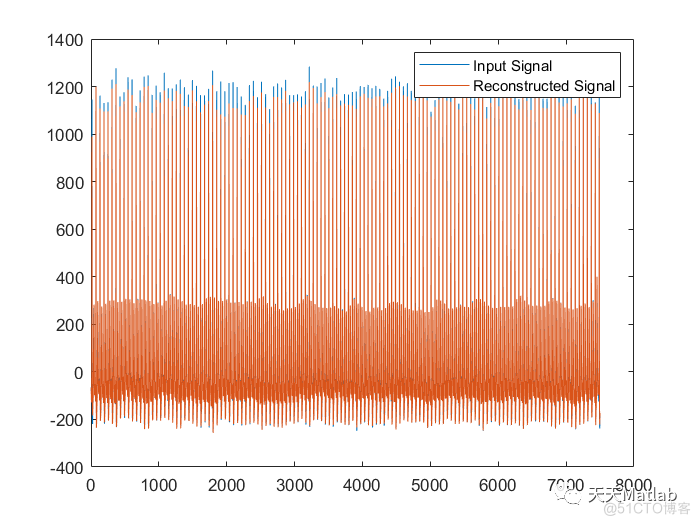
plot(signal)
hold on
plot(sum(u))
legend('Input Signal','Reconstructed Signal')
figure
subplot(211)
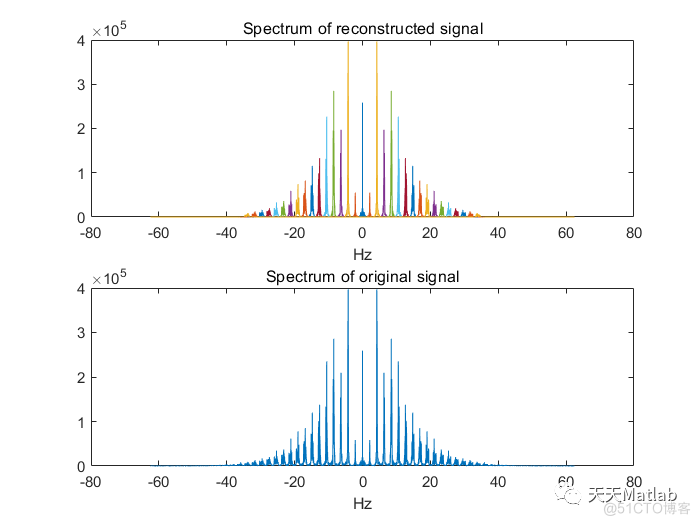
plot(omega_freqs*fs,abs(uhat))
title('Spectrum of reconstructed signal')
xlabel('Hz')
subplot(212)
plot(omega_freqs*fs,abs(f_hat))
title('Spectrum of original signal')
xlabel('Hz')
%% Example 2 (EEG signal)
%
% load('EEG.mat');
% signal=double(eeg (1,:));
%
%
% %% Initialization
% maxAlpha=1000; %compactness of mode
% tau=0;%time-step of the dual ascent
% tol=1e-6; %tolerance of convergence criterion;
% stopc=1;%the type of stopping criteria
%
% fs=200; % sampling frequency
% T = length(signal);% time domain (t -->> 0 to T)
% t = (1:T)/T;
% omega_freqs = t-0.5-1/T;%discretization of spectral domain
% f_hat=fftshift(fft(signal));
%
% [u,uhat]=svmd(signal,maxAlpha,tau,tol,stopc);
%
% plot(signal)
% hold on
% plot(sum(u))
% legend('Input Signal','Reconstructed Signal')
%
% figure
% subplot(211)
% plot(omega_freqs*fs,abs(uhat))
% title('Spectrum of reconstructed signal')
% xlabel('Hz')
% subplot(212)
% plot(omega_freqs*fs,abs(f_hat))
% title('Spectrum of original signal')
% xlabel('Hz')
%⛄ 运行结果
⛄ 参考文献
[1] 叶剑华,曹旌,杨理,等.基于变分模态分解和多模型融合的用户级综合能源系统超短期负荷预测[J].电网技术, 2022(007):046.
[2] 赵亚军,窦远明,张明杰.基于变分模态分解的模态参数识别研究[J].振动与冲击, 2020, 39(2):8.DOI:CNKI:SUN:ZDCJ.0.2020-02-017.