先考虑这么一个问题:
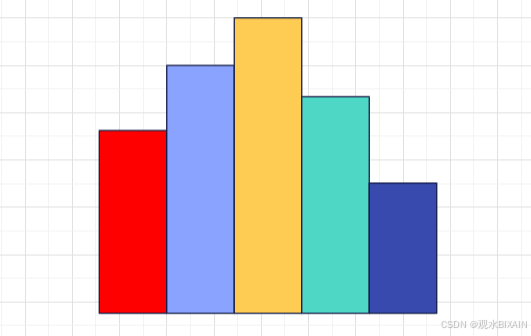
如何求出一个序列在所有位置上的各个元素的前面和后面第一个比它小的元素位置。
显然这个问题可以用单调栈来解决。
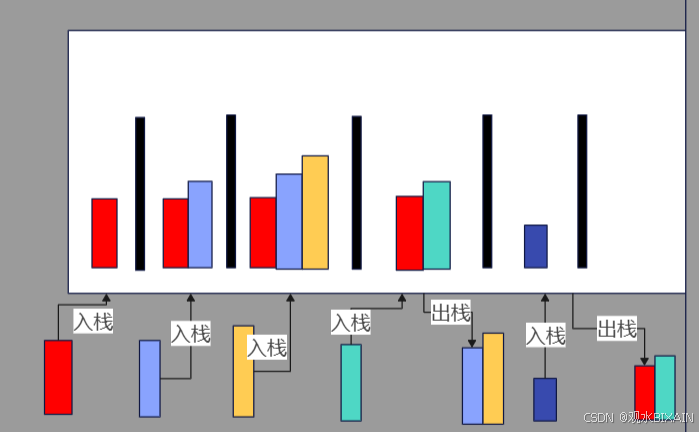
如上图所示,维护一个单调递增的序列,每当栈顶>当前元素时,就抛出栈顶,这时就找到了栈顶元素后面第一个小于它的元素,以此循环,就能找到所有位置上的元素后面第一个比它小的元素位置。要找到前面第一个小的元素位置只要反正入栈即可。
每个元素至多入栈和出栈各一次,时间复杂程度为O(N)。
----------------------------------------------------------------------------------------------------------------------------
然后我们考虑这个问题:
如何求出一个动态序列在询问位置上的元素在询问时刻的前面和后面第一个比它小的元素位置。(每次插入元素的位置可在序列的前中后的任意位置)。
若每次询问时都跑一边单调栈,时间复杂程度为(NQ),其中Q为询问次数。
现考虑以下数据结构:
将每一个连续的上升或下降序列定义为一个breand,breand的指针指向峰顶和谷底(t1,t2)。
每个元素(圆点)有4个指针p1,p2,le,ri,若在上升序列用p2指向breand,下降用p1,峰顶和谷地可以同时使用p1,p2;用le,ri指向相邻元素。
每个breand都是有序不重复序列,使用set结构存储元素大小,查找元素大小时间复杂度为O(logn)。(连续相同的元素会合在一起为一个元素,元素.size++)
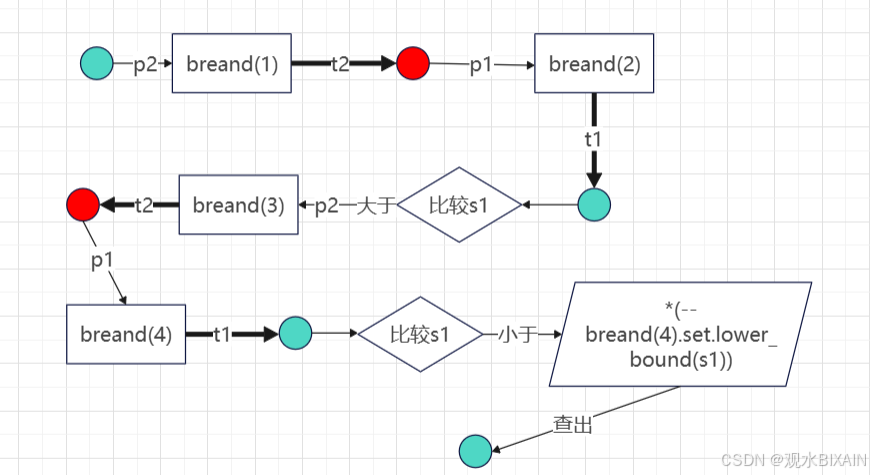
下面给出s1元素(左下角箭头所指元素)查找后面第一个小于它的元素(s10)的位置的过程:
s1-->s1.p2-->breand(1)-->t2-->s4-->s4.p1-->breand(2)-->t1-->s6
-->(比较s6>=s1)-->s6.p2-->breand(3)-->t2-->s8-->s8.p1-->breand(4)
-->t1->s10-->(比较s10<s1)-->*(--breand(4).set.lower_bound(s1))-->s10。
因此查完所有询问元素的复杂程度为O(Q(K+logM))。
其中K为直接通过谷底比较跳过的breand数,M为最后一个breand的元素个数。
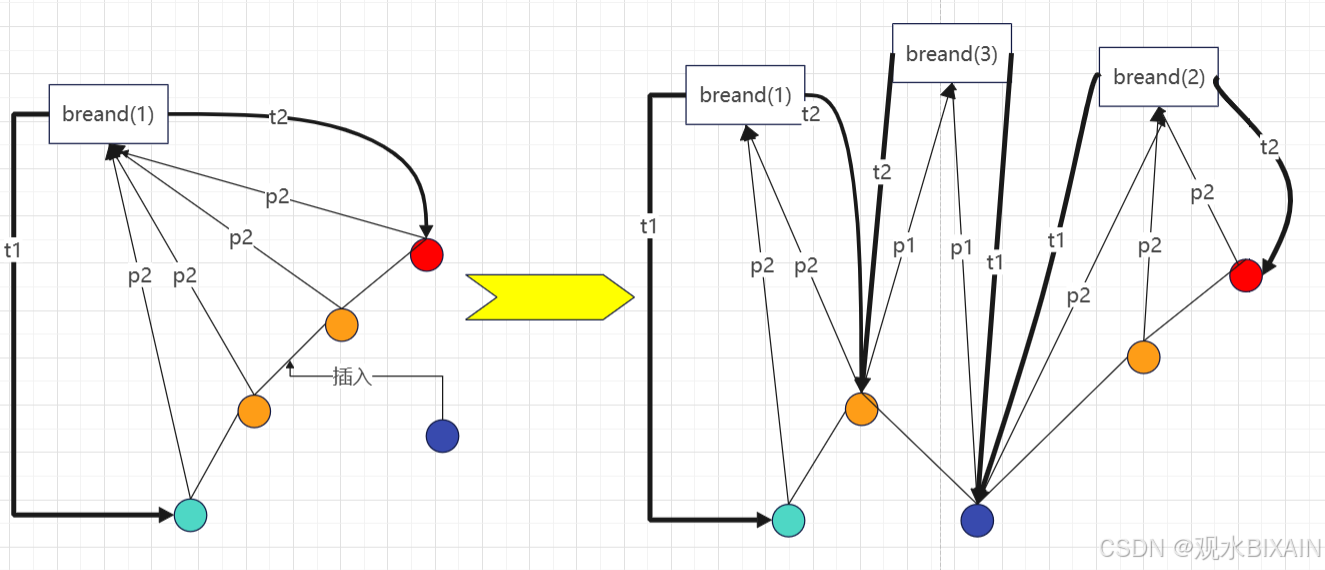
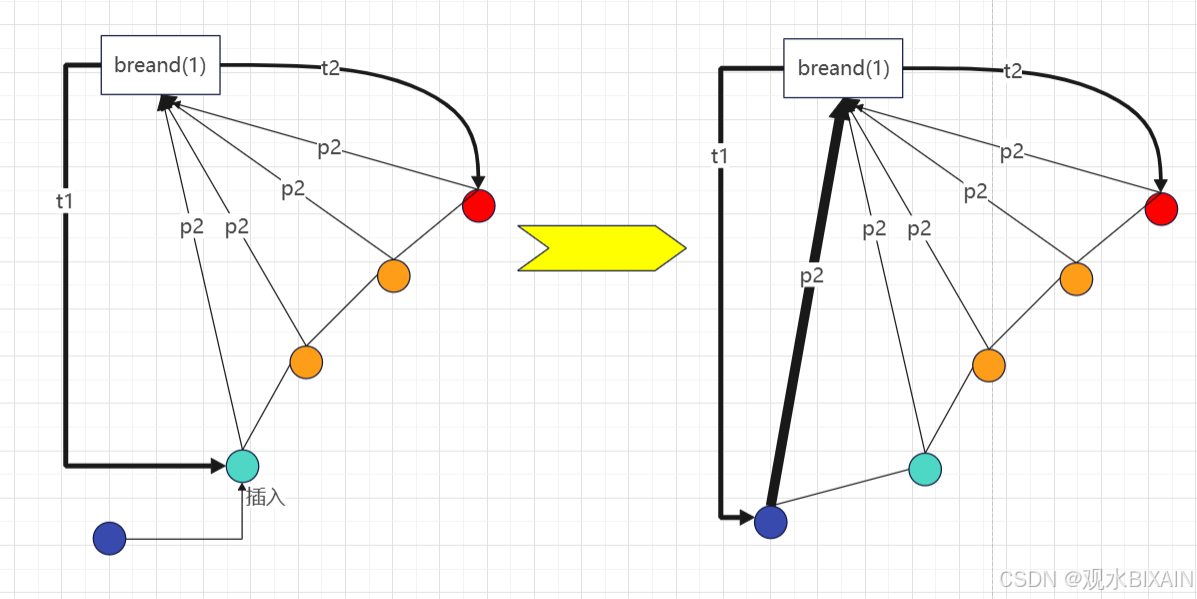
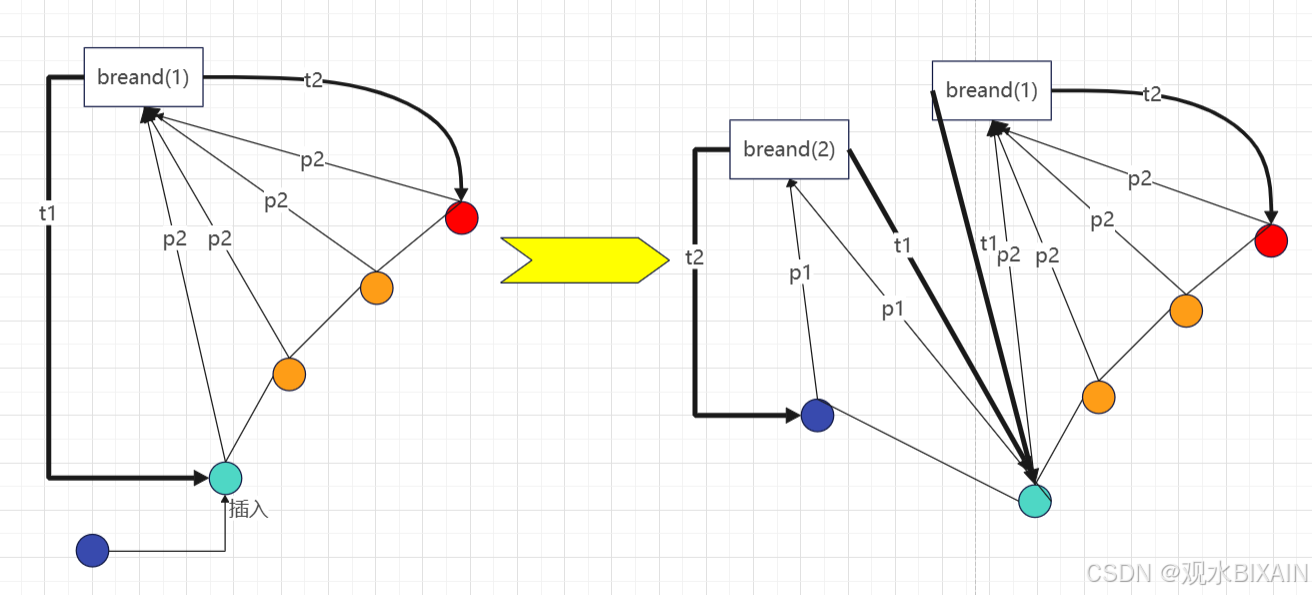
下面给出该数据结构的元素插入过程(主要分4种情况):
(1)中间不破顺序插入
(2)中间破顺序插入
(3)两端不破顺序插入
(4)两端破顺序插入
插入所有元素的复杂程度期望为O( N(logM)^2 )。其中M为breand中的元素个数期望。
因此算法总复杂程度为O(Q(K+logM)+N(logM)^2 )。
其中K为直接通过谷底比较跳过的breand数的期望,M为breand中的元素个数期望,Q为询问次数,N为元素个数。
以下为代码:(插入元素部分的代码占了大部分)(查找的是元素前面和后面最后一个不比它小的元素位置)
struct line
{
struct po
{
ll value,size;
ll p1=0,p2=0,le,ri;
ll tag;
po(ll a=0,ll b=0,ll c=-1,ll d=-1,ll f=0){value=a,size=b,le=c,ri=d,tag=f;}
};
struct pa
{
ll value,loc;
pa(ll a,ll b){value=a,loc=b;};
bool operator<(const pa &b)const
{
return value<b.value;
}
};
struct brean
{
ll p1=0,p2=0;
set<pa>se;
};
ll len = 0,cnt=0;
vector<po>s;
vector<brean>ff;
set<ll>dk;
line(ll n) :len(n), s(n + 1), ff(n + 1) {dk.insert(-1);};
pair<ll,ll> lin_find(ll loc)
{
ll le_ve=loc,ri_ve=loc;
if(s[loc].ri!=-1&&s[loc].value<s[s[loc].ri].value)
{
ll yy=s[ff[s[loc].p2].p2].p1;
while(ff[yy].p1&&s[ff[yy].p1].value>=s[loc].value)
yy=s[ff[s[ff[yy].p1].p2].p2].p1;
if(ff[yy].p1)
ri_ve=(*(ff[yy].se.lower_bound(pa(s[loc].value,loc)))).loc;
else
ri_ve=ff[yy].p2;
}
if(s[loc].le!=-1&&s[loc].value<s[s[loc].le].value)
{
ll yy=s[ff[s[loc].p1].p2].p2;
while(ff[yy].p1&&s[ff[yy].p1].value>=s[loc].value)
yy=s[ff[s[ff[yy].p1].p1].p2].p2;
if(ff[yy].p1)
le_ve=(*(ff[yy].se.lower_bound(pa(s[loc].value,loc)))).loc;
else
le_ve=ff[yy].p2;
}
pair<ll,ll> a1(le_ve,ri_ve);
return a1;
}
void lin_insert(ll loc,ll ve)
{
auto p1=dk.lower_bound(loc);
auto p3=p1;
auto p2=--p3;
if(p1==dk.end()&&p2==dk.begin())
{
s[loc]=po(ve,1,-1,-1,3);
dk.insert(loc);
return;
}
if(p1!=dk.end()&&s[*p1].value==ve)
{
s[*p1].size++;
return;
}
if(p2!=dk.begin()&&s[*p2].value==ve)
{
s[*p2].size++;
return;
}
if(ve>max(p1!=dk.end()?s[*p1].value:-1e10,p2!=dk.begin()?s[*p2].value:-1e10))
{
if(p1!=dk.end()&&(s[*p1].tag==2||s[*p1].tag==3))
{
s[loc]=po(ve,1,p2!=dk.begin()?*p2:-1,*p1,2);
s[*p1].le=loc;
if(p2!=dk.begin())s[*p2].ri=loc;
s[loc].p1=s[*p1].p1;
s[loc].p2=s[*p1].p2;
if(s[*p1].p1)
{
ff[s[*p1].p1].p2=loc;
ff[s[*p1].p1].se.insert(pa(ve,loc));
}
else
{
ff[++cnt].p2=loc;
ff[cnt].p1=*p1;
s[loc].p1=s[*p1].p1=cnt;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
}
if(s[*p1].p2)
{
ff[s[*p1].p2].p2=loc;
ff[s[*p1].p2].se.erase(pa(s[*p1].value,*p1));
ff[s[*p1].p2].se.insert(pa(ve,loc));
s[*p1].p2=0;
}
if(s[*p1].ri!=-1)
s[*p1].tag=0;
else
s[*p1].tag=1;
dk.insert(loc);
return;
}
if(p2!=dk.begin()&&(s[*p2].tag==2||s[*p2].tag==3))
{
s[loc]=po(ve,1,*p2,p1!=dk.end()?*p1:-1,2);
s[*p2].ri=loc;
if(p1!=dk.end())s[*p1].le=loc;
s[loc].p1=s[*p2].p1;
s[loc].p2=s[*p2].p2;
if(s[*p2].p2)
{
ff[s[*p2].p2].p2=loc;
ff[s[*p2].p2].se.insert(pa(ve,loc));
}
else
{
ff[++cnt].p2=loc;
ff[cnt].p1=*p2;
s[loc].p2=s[*p2].p2=cnt;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
}
if(s[*p2].p1)
{
ff[s[*p2].p1].p2=loc;
ff[s[*p2].p1].se.erase(pa(s[*p2].value,*p2));
ff[s[*p2].p1].se.insert(pa(ve,loc));
s[*p1].p1=0;
}
if(s[*p2].le!=-1)
s[*p2].tag=0;
else
s[*p2].tag=1;
dk.insert(loc);
return;
}
if(p1!=dk.end()&&p2!=dk.begin())
{
cnt++;
ff[cnt].p2=loc;
s[loc]=po(ve,1,*p2,*p1,2);
s[*p2].ri=s[*p1].le=loc;
if(s[*p1].value>s[*p2].value)
{
s[loc].p2=cnt;
ff[cnt].p1=ff[s[*p2].p2].p1;
ff[cnt].se.insert(pa(ve,loc));
ll yy=*p2;
while(yy!=ff[cnt].p1)
{
ff[s[yy].p2].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p2=cnt;
yy=s[yy].le;
}
ff[s[yy].p2].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p2=cnt;
ff[++cnt].p2=loc;
ff[cnt].p1=*p1;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
s[loc].p1=s[*p1].p1=cnt;
s[*p1].tag=1;
}
else
{
s[loc].p1=cnt;
ff[cnt].p1=ff[s[*p1].p1].p1;
ff[cnt].se.insert(pa(ve,loc));
ll yy=*p1;
while(yy!=ff[cnt].p1)
{
ff[s[yy].p1].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p1=cnt;
yy=s[yy].ri;
}
ff[s[yy].p1].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p1=cnt;
ff[++cnt].p2=loc;
ff[cnt].p1=*p2;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
s[loc].p2=s[*p2].p2=cnt;
s[*p2].tag=1;
}
dk.insert(loc);
}
else if(p1!=dk.end())
{
s[loc]=po(ve,1,-1,*p1,2);
s[*p1].le=loc;
ff[++cnt].p2=loc;
ff[cnt].p1=*p1;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
s[loc].p1=s[*p1].p1=cnt;
s[*p1].tag=1;
dk.insert(loc);
}
else
{
s[loc]=po(ve,1,*p2,-1,2);
s[*p2].ri=loc;
ff[++cnt].p2=loc;
ff[cnt].p1=*p2;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
s[loc].p2=s[*p2].p2=cnt;
s[*p2].tag=1;
dk.insert(loc);
}
}
else if(ve<min(p1!=dk.end()?s[*p1].value:1e10,p2!=dk.begin()?s[*p2].value:1e10))
{
if(p1!=dk.end()&&(s[*p1].tag==1||s[*p1].tag==3))
{
s[loc]=po(ve,1,p2!=dk.begin()?*p2:-1,*p1,1);
s[*p1].le=loc;
if(p2!=dk.begin())s[*p2].ri=loc;
s[loc].p1=s[*p1].p1;
s[loc].p2=s[*p1].p2;
ff[s[*p1].p1].p1=loc;
ff[s[*p1].p2].p1=loc;
if(s[*p1].p2)
{
ff[s[*p1].p2].p1=loc;
ff[s[*p1].p2].se.insert(pa(ve,loc));
}
else
{
ff[++cnt].p1=loc;
ff[cnt].p2=*p1;
s[loc].p2=s[*p2].p2=cnt;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
}
if(s[*p1].p1)
{
ff[s[*p1].p1].p1=loc;
ff[s[*p1].p1].se.erase(pa(s[*p1].value,*p1));
ff[s[*p1].p1].se.insert(pa(ve,loc));
s[*p1].p1=0;
}
if(s[*p1].ri!=-1)
s[*p1].tag=0;
else
s[*p1].tag=2;
dk.insert(loc);
return;
}
if(p2!=dk.begin()&&(s[*p2].tag==1||s[*p2].tag==3))
{
s[loc]=po(ve,1,*p2,p1!=dk.end()?*p1:-1,1);
s[*p2].ri=loc;
if(p1!=dk.end())s[*p1].le=loc;
s[loc].p1=s[*p2].p1;
s[loc].p2=s[*p2].p2;
if(s[*p2].p1)
{
ff[s[*p2].p1].p1=loc;
ff[s[*p2].p1].se.insert(pa(ve,loc));
}
else
{
ff[++cnt].p1=loc;
ff[cnt].p2=*p2;
s[loc].p1=s[*p2].p1=cnt;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
}
if(s[*p2].p2)
{
ff[s[*p2].p2].p1=loc;
ff[s[*p2].p2].se.erase(pa(s[*p2].value,*p2));
ff[s[*p2].p2].se.insert(pa(ve,loc));
s[*p1].p2=0;
}
if(s[*p2].le!=-1)
s[*p2].tag=0;
else
s[*p2].tag=2;
dk.insert(loc);
return;
}
if(p1!=dk.end()&&p2!=dk.begin())
{
cnt++;
ff[cnt].p1=loc;
s[loc]=po(ve,1,*p2,*p1,1);
s[*p2].ri=s[*p1].le=loc;
if(s[*p1].value>s[*p2].value)
{
s[loc].p2=cnt;
ff[cnt].p2=ff[s[*p1].p2].p2;
ff[s[*p1].p2].p2=*p2;
ff[cnt].se.insert(pa(ve,loc));
ll yy=*p1;
while(yy!=ff[cnt].p2)
{
ff[s[yy].p2].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p2=cnt;
yy=s[yy].ri;
}
ff[s[yy].p2].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p2=cnt;
ff[++cnt].p1=loc;
ff[cnt].p2=*p2;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
s[loc].p1=s[*p2].p1=cnt;
s[*p2].tag=2;
}
else
{
s[loc].p1=cnt;
ff[cnt].p2=ff[s[*p2].p1].p2;
ff[s[*p2].p1].p2=*p1;
ff[cnt].se.insert(pa(ve,loc));
ll yy=*p2;
while(yy!=ff[cnt].p2)
{
ff[s[yy].p1].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p1=cnt;
yy=s[yy].le;
}
ff[s[yy].p1].se.erase(pa(s[yy].value,yy));
ff[cnt].se.insert(pa(s[yy].value,yy));
s[yy].p1=cnt;
ff[++cnt].p1=loc;
ff[cnt].p2=*p1;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
s[loc].p2=s[*p1].p2=cnt;
s[*p1].tag=1;
}
dk.insert(loc);
}
else if(p1!=dk.end())
{
s[loc]=po(ve,1,-1,*p1,1);
s[*p1].le=loc;
ff[++cnt].p1=loc;
ff[cnt].p2=*p1;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p1].value,*p1));
s[loc].p2=s[*p1].p2=cnt;
s[*p1].tag=2;
dk.insert(loc);
}
else
{
s[loc]=po(ve,1,*p2,-1,1);
s[*p2].ri=loc;
ff[++cnt].p1=loc;
ff[cnt].p2=*p2;
ff[cnt].se.insert(pa(ve,loc));
ff[cnt].se.insert(pa(s[*p2].value,*p2));
s[loc].p1=s[*p2].p1=cnt;
s[*p2].tag=2;
dk.insert(loc);
}
}
else
{
s[loc]=po(ve,1,*p2,*p1,0);
s[*p1].le=s[*p2].ri=loc;
ff[s[*p1].p2].se.insert(pa(ve,loc));
if(s[*p1].value>s[*p2].value)
s[loc].p2=s[*p1].p2;
else
s[loc].p1=s[*p1].p1;
dk.insert(loc);
}
}
};以下是叠甲:这个数据结构是我做题时突发奇想的,但我没有找到合适的题来试它,没有找到类似的动态插入查找问题,只能找到静态的题目来试试它的复杂程度对不对,根据洛谷p2422这个静态题目复杂程度大致是对的。
如果这个数据结构有名字或有差不多的,欢迎指正(看书可能少了)。
后面可能我会往平衡树,红黑树之类的方面看看继续优化一下,这个感觉还有空间,无用的操作还是多了。
提示:代码上为了适配试验的静态题目,用了预制的插入位+离散化来模拟;插入部分的代码大多是p1,p2两个轮换,结构都是差不多的(但是我懒得写封装函数优化了);注释我有时间会加上。
错误的地方欢迎指正,当然也欢迎点赞。