总结一下算法吧,工程量有点大,准备慢慢更,现在上面写的算法和例题都是比较基础的,后续记得加深点难度(说给自己)
目录
排序
这里写的所有排序都是升序排序
冒泡排序
每一趟下来,把最大的数放在最右边
void BubbleSort(int*a,int n)
{
for(int i=n-1;i>0;i--)
{
for(int j=0;j<i;j++)
{
if(a[j]>a[j+1])
{
int t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
} 选择排序
每一趟下来,把最小的数放在最左边
void SelectSort(int*a,int n)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(a[i]>a[j])
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
}
}
}
起泡法
鸡尾酒排序
桶排序
计数排序
归并排序
排序二叉树
鸽巢排序
基数排序
希尔排序
不断对半进行两两排序
void ShellSort(int *arr, int n)
{
int gap = n;
while (gap>1)
{
//每次对gap折半操作
gap = gap / 2;
//单趟排序
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tem = arr[end + gap];
while (end >= 0)
{
if (tem < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end+gap] = tem;
}
}
}
堆排序
具体可看这篇博客http://t.csdn.cn/gwoTF
快速排序
从第二个数起,不断地与前面的数比较,如果这个数比前面的数小,则继续往前移,否则就把这个数放在那里
void InsertSort(int*a,int n)
{
for(int i=0;i<n;i++)
{
int t=a[i+1];
for(int j=i;j>=0;j--)
{
if(t<a[j])
{
a[j+1]=a[j]
}
else
break;
}
a[j+1]=t;
}
}
树形选择排序
搜索
深度优先搜索(DFS)
一般用于解决一些最大、最长或所有可能的问题,多用递归算法
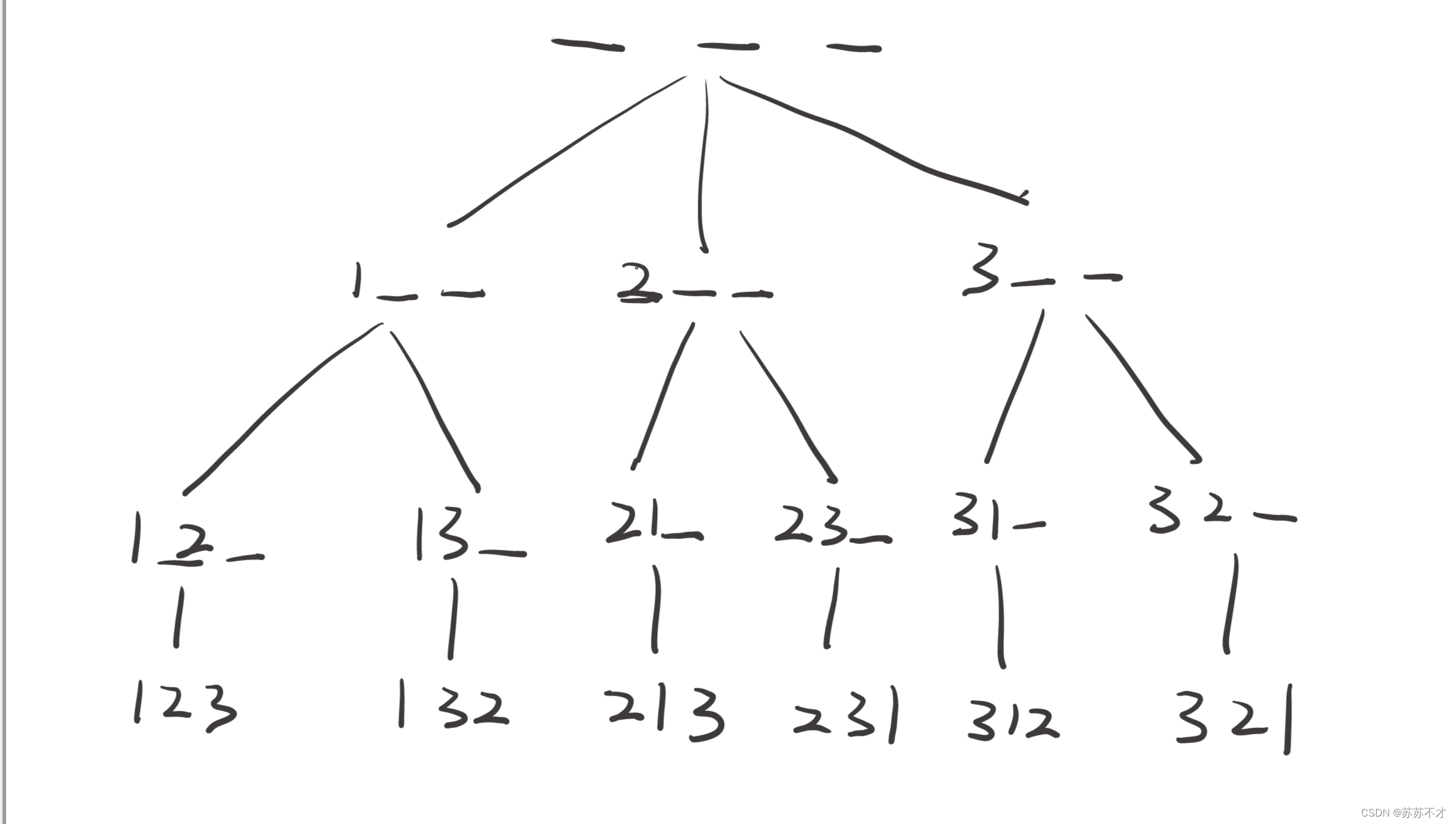
看下面的例题:
算法流程:
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
//path数组存储每次到底层的路径
int path[N];
//布尔数组存储每次已经遍历的点,默认是false
bool st[N];
int n;
//u表示当前的层数
void dfs(int u)
{
//当已经到达最底层了,溯回并输出路径
if( u == n )
{
for(int i = 0 ; i < n ; i++) printf("%d " , path[i] );
//作用跟printf("%s\n",s),默认帮你换行
puts("");
//溯回上一层
return;
}
else
{
//这里从第一个数开始循环
for(int i = 1; i <= n ; i++)
{
//如果该数字未被访问,就使用
if( !st[i] )
{
path[u] = i;
//标记第i个数已经被使用
st[i] = true;
//进入下一层
dfs( u + 1 );
//还原现场
st[i] = false;
}
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}
宽度优先搜索(BFS)
系统地展开并检查图中的所有节点,以找寻结果。
例题:迷宫问题
#include <iostream>
using namespace std;
char a[100][100];
int n,m,v[100][100]={0};/**< v标志数组,同时也用于记录步数 */
int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0};
void bfs(int x,int y)
{
int i,j;/**< 两个队列qx,qy分别存储横纵坐标 */
int qx[100005],qy[100005],fx=0,rx=0,fy=0,ry=0;
qx[rx++]=1,qy[ry++]=1;/**< */
v[1][1]=1;/**< 迷宫起点步数记为1 */
while(fx!=rx)
{
x=qx[fx++],y=qy[fy++];
for(i=0;i<4;i++)
{
int newx=x+dx[i],newy=y+dy[i];/**< bfs三要素,合法性+可访问+未标记 */
if(newx>=1&&newx<=n&&newy>=1&&newy<=m&&a[newx][newy]=='0'&&v[newx][newy]==0)
{
v[newx][newy]= v[x][y]+1;/**< 因为(newx,newy)是从(x,y)走一步到达,因为步数+1 */
qx[rx++]=newx,qy[ry++]=newy;
}
}
}
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0);
int i,j;
cin>>n>>m;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
cin>>a[i][j];
bfs(1,1);
cout<<v[n][m]-1;
return 0;
}
启发式搜索
概念:
利用启发信息定义节点的启发函数h(n),使用数据结构:OPEN表,CLOSED表
启发函数
f(n)=g(n)+h(n)
f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时,我们总会选取综合优先级最高(值最小)的节点。g(n) 是节点n距离起点的代价。h(n)是节点n距离终点的预计代价
常见的五种启发式算法有:遗传算法,粒子群算法,蚁群算法,禁忌搜索,模拟退火
八数码问题:
问题描述:通过单步移动把下面的矩阵移动成1-8环绕一周的矩阵(即0在中间,1-8顺序排成一圈,1在哪无所谓)
(1) 分别用宽度和深度搜索进行;
(2) 假设启发式的方程为f(n)=d(n)+h(n),其中d(n)为层次或深度,h(n)为错误的个数,使用启发式算法解决;
(3) 编程(分别用宽度搜索,深度搜索和启发式算法),并分析步数。
1.open表存初始状态以及初始状态的更新
2.closed表存在变化过程中的状态,从而计算其同目标状态所差的格数是不是最小,找出在变换过程中所差格数最小的状态,其他的丢弃
3.为了便于记录并比较每个状态,我们在处理时将数组转换成字符串a处理,这样在对照比较时就是看字符串的每一位是否相同,若不同,则所差格子数即id[a]++;指在a这个字符串状态时所差的格子数
4.
#include<iostream>
#include<queue>
#include<map>
#include<stack>
using namespace std;
map<int, int>vis;
map<int, int>step;
map<int, int>id;
map<int, int>parent;
queue<int>open;
queue<int>close;
queue<int>nclose;
stack<int>out;
int m, n;
int dir[4][2] = { 0,-1,-1,0,0,1,1,0 }; //左、上、右、下
int change(int**p) //把数组转为数字
{
int s = 0;
for(int i=0;i<m;i++)
for (int j = 0; j < n; j++)
s = s * 10 + p[i][j];
return s;
}
void getid(int a,int b) //获取与目标状态不同的格子数
{
int c;
c = a;
for (int i = 0; i < m * m; i++)
{
if ((a % 10) != (b % 10))
id[c]++;
a = a / 10, b = b / 10;
}
}
int A (int u,int v) //启发式搜索
{
open.push(u); //把初始状态放进open表中
vis[u] = 1; //标记该状态已被访问
getid(u, v); //获取该状态与目标状态不同的格子数
while (open.size()) //open表为空结束搜索
{
int q, p, w, x, y, newx, newy, size;
if (open.front() == v) //找到目标状态
return step[v];
size = open.size();
for(int i=0;i<size;i++) //找出该层数中,最小的id值
{
int** r;
w=q=open.front(); //取出表头元素
open.pop();
r = new int* [n];
for (int i = 0; i < n; i++)
r[i] = new int[m];
for (int i = m - 1; i >= 0; i--) //找到空白格位置
for (int j = n - 1; j >= 0; j--)
{
r[i][j] = q % 10, q = q / 10;
if (r[i][j] == 0)
{
x = i, y = j; //标记空白格位置
}
}
for (int i = 0; i < 4; i++) //搜索该状态的四个方向
{
newx = x + dir[i][0], newy = y + dir[i][1];
if (newx >= 0 && newx < m && newy >= 0 && newy < n) //若该位置可交换
{
r[x][y] = r[newx][newy]; //交换空白格位置
r[newx][newy] = 0;
p = change(r);
if (!vis[p]) //该状态没有被访问过
{
close.push(p); //把该状态放进close表
nclose.push(p);
vis[p] = 1;
step[p] = step[w] + 1; //层数在原来状态上加一
parent[p] = w; //标记父状态
getid(p, v);
}
r[newx][newy] = r[x][y]; //变回原来状态
r[x][y] = 0; //一直到这里算是一次深搜
}
}
}
if (close.size()) //若close表不为空
{
int csize = close.size(), min;
min = id[nclose.front()];
for (int i = 0; i < csize; i++) //找出close表中id的最小值
if (id[nclose.front()] < min)
{
min = id[nclose.front()];
nclose.pop();
}
else nclose.pop();
for (int i = 0; i < csize; i++) //把close表中id最小值的状态放进open表中
if (id[close.front()] == min)
{
open.push(close.front());
close.pop();
}
else close.pop();
}
}
return -1;
}
int main()
{
cout << "A搜索" << endl;
int u, v, t;
int** mau, ** mav;
cout << "输入m*n:" << endl;
cin >> m >> n;
mau = new int* [n], mav = new int* [n];
for (int i = 0; i < n; i++)
mau[i] = new int[m], mav[i] = new int[m];
cout << "输入初始状态:" << endl;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
cin >> mau[i][j];
cout << "输入最终状态:" << endl;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
cin >> mav[i][j];
u = change(mau), v = change(mav);
if (A(u, v) != -1)
{
cout << "到达目标状态需要 " << A(u, v) << " 步" << endl;
t = v;
while (t)
{
out.push(t);
t = parent[t];
}
while (out.size()) //输出到达目标状态的过程
{
int** o;
t = out.top();
out.pop();
o = new int* [n];
for (int i = 0; i < n; i++)
o[i] = new int[m];
for (int i = m - 1; i >= 0; i--)
for (int j = n - 1; j >= 0; j--)
o[i][j] = t % 10, t /= 10;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
cout << o[i][j] << " ";
cout << endl;
}
cout << "======" << endl;
}
}
else cout << "无解" << endl;
}