二叉树
二叉树的遍历
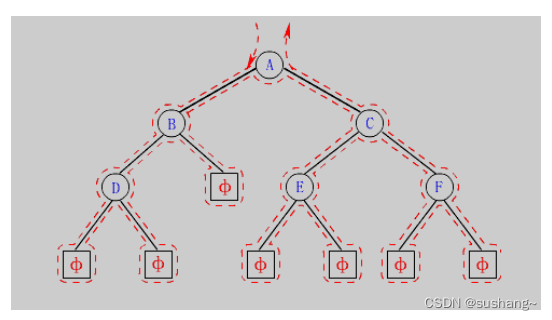
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
二叉树的结构体创建
二叉树结构体内容包括数据,左指针和右指针
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
二叉树节点的创建
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
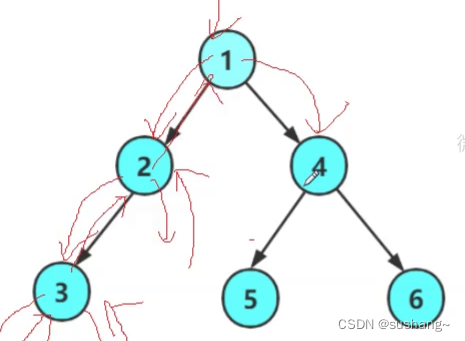
二叉树的创建
将节点1的左指针链接节点2,节点1的右指针链接节点4,节点2的左指针链接节点3,节点4的左指针链接节点5,节点4的右指针链接节点6,最后返回节点1的指针
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
创建结果如上图所示
二叉树的前序遍历
先访问根节点的数据,再访问左子树,再访问右子树
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
二叉树的中序遍历
先访问左子树,再访问根节点的数据,再访问右子树
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
二叉树的后序遍历
先访问左子树,再访问右子树,再访根节点的数据
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
二叉树节点的个数
统计左子树的节点个数+右子树的节点个数+1(根节点的个数)
//遍历计数
//int size = 0;
//void BTreeSize(BTNode* root)
//{
// if (root == NULL)
// return;
// ++size;
// BTreeSize(root->left);
// BTreeSize(root->right);
//}
//分治思维
int BTreeSize(BTNode* root)
{
/*if (root == NULL)
return 0;
return BTreeSize(root->left) + BTreeSize(root->right) + 1;*/
return root==NULL?0: BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
二叉树叶子节点的个数
如果根为空,则返回0,如果左子树为空且右子树为空,则返回1,最后统计左子树的叶子节点个数+右子树的叶子节点个数
int BTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
二叉树的高度
int BTreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int leftHeight = BTreeHeight(root->left);
int rightHeight = BTreeHeight(root->right);
return leftHeight > rightHeight ?
leftHeight + 1 : rightHeight + 1;
}
二叉树第K层节点的个数
如果根为空,则返回0,如果是第一层,返回1,最后返回左子树的第k-1层+右子树的第k-1层
int BTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BTreeLevelKSize(root->left, k - 1) + BTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
如果根为空,则返回0;如果根的值为x,返回根结点;如果左子树中有结点为x的,则返回左子树的那个结点;如果右子树中有结点为x的,则返回右子树的那个结点。
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret1 = BTreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = BTreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
/*return BTreeFind(root->right, x);*/
}
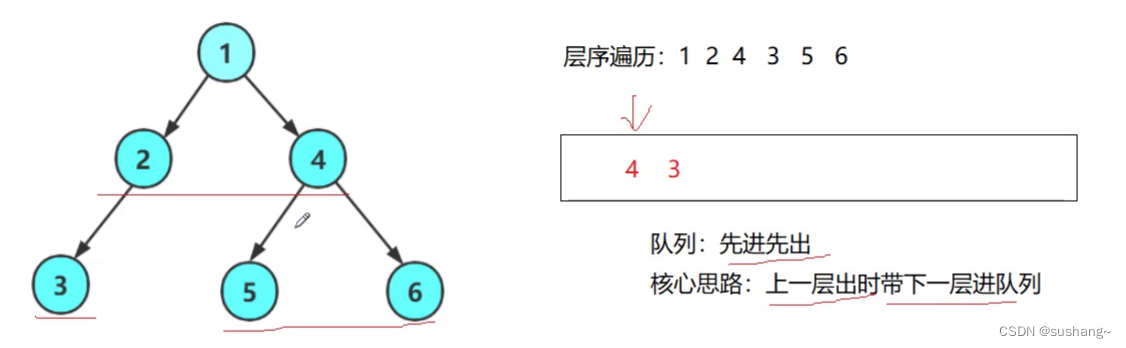
二叉树的层序遍历
层序遍历是一层一层访问,先访问第一层1,再访问第二层2,4,再访问第三层3,5,6
void LeveOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
二叉树的销毁
如果根为空,直接返回,否则先访问
void BTreeDestroy(BTNode* root)
{
if (root == NULL)
return;
BTreeDestroy(root->left);
BTreeDestroy(root->right);
free(root);
}
判断二叉树是否为完全二叉树
bool BTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//遇到空就跳出
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查后面的节点有没有非空
//有非空,不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
堆的测试主函数
int main()
{
//BTNode* root = CreatBinaryTree();
PostOrder(root);
printf("\n");
//BTreeSize(root);
//printf("BTreeSize:%d\n", BTreeSize(root));
size = 0;
//BTreeSize(root);
//printf("BTreeSize:%d\n", BTreeSize(root));
size = 0;
//BTreeSize(root);
//printf("BTreeSize:%d\n", BTreeSize(root));
BTNode* root = CreatBinaryTree();
//PostOrder(root);
//printf("\n");
BTreeLeafSize(root);
printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));
//size = 0;
BTreeLeafSize(root);
printf("BTreeLeafSize:%d\n", BTreeLeafSize(root));
//size = 0;
BTreeHeight(root);
printf("BTreeHeight:%d\n", BTreeHeight(root));
BTreeLevelKSize(root,2);
printf("BTreeLevelKSize:%d\n", BTreeLevelKSize(root,2));
//LevelOrder(root);
printf("BTreeComplete:%d\n", BTreeComplete(root));
BTreeDestroy(root);
root = NULL;
return 0;
}
队列的头文件 Queue.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdbool.h>
#include<stdlib.h>
typedef struct BinaryTreeNode* QDataType;
//typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QNode;
typedef struct Queue
{
QNode* phead;
QNode* ptail;
int size;
}Queue;
//初始化
void QueueInit(Queue*pq);
//销毁
void QueueDestroy(Queue* pq);
//插入数据
void QueuePush(Queue* pq, QDataType x);
//删除数据
void QueuePop(Queue* pq);
//返回队头
QDataType QueueFront(Queue* pq);
//返回队尾
QDataType QueueBack(Queue* pq);
//返回大小
int QueueSize(Queue* pq);
//判断是否为空
bool QueueEmpty(Queue* pq);
队列的实现 Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
void QueueInit(Queue* pq)
{
assert(pq);
pq->phead = NULL;
pq->ptail = NULL;
pq->size= 0;
}
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->phead;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->phead = pq->ptail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail\n");
return;
}
newnode->data = x;
newnode->next = NULL;
if (pq->ptail == NULL)
{
assert(pq->phead==NULL);
pq->phead = pq->ptail = newnode;
}
else
{
pq->ptail->next = newnode;
pq->ptail = newnode;
}
pq->size++;
}
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
//1.一个节点
//2.多个节点
if (pq->phead->next == NULL)
{
free(pq->phead);
pq->phead = pq->ptail = NULL;
}
else
{
//头删
QNode* next = pq->phead->next;
free(pq->phead);
pq->phead = next;
}
pq->size--;
}
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->ptail->data;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
//return pq->phead == NULL&&pq->ptail==NULL;
return pq->size == 0;
}