一、问题定义
1.1 实例引入
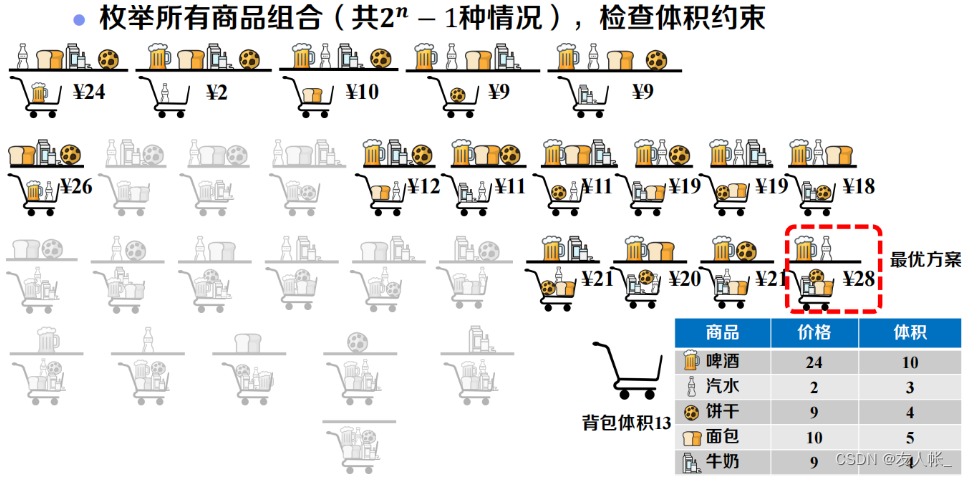
若超市允许顾客使用一个体积大小为13的背包,选择一件或多件商品带走,则如何选择可以使得收益最高?
| 商品 | 价格 | 体积 |
|---|---|---|
| 啤酒 | 24 | 10 |
| 汽水 | 2 | 3 |
| 饼干 | 9 | 4 |
| 面包 | 10 | 5 |
| 牛奶 | 9 | 4 |
1.2 形式化定义
0-1 Knapsack Problem
输入:
\quad - n n n个商品组成集合 O O O,每个商品有属性价格 p i p_i pi和体积 v i v_i vi
\quad - 背包容量为 C C C
输出:
\quad - 求解一个商品子集 S ⊆ O S\subseteq O S⊆O,使得
\quad \quad 优化目标: m a x ∑ i ∈ S p i max\sum_{i \in S}p_i max∑i∈Spi
\quad \quad 约束条件: ∑ i ∈ S v i ≤ C \sum_{i \in S}v_i\leq C ∑i∈Svi≤C
二、问题求解
2.1 蛮力枚举
很自然的想法便是将所有商品一一列举出来,然后将不符合容量限制的组合去掉,在剩余中找到最大值,即为最优方案。
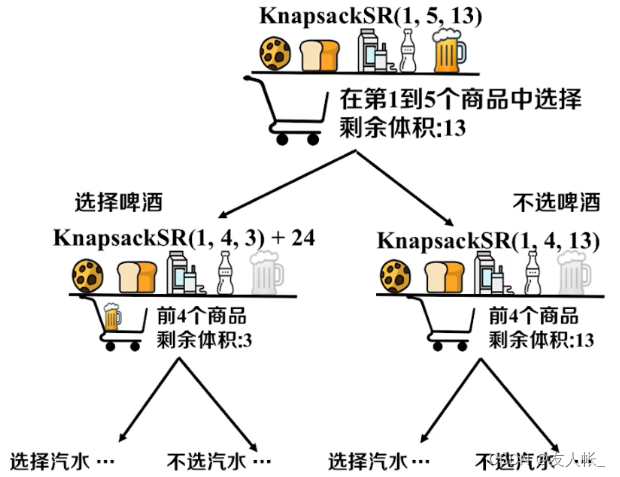
定义递归函数:
K n a p s a c k S R ( h , i , c ) KnapsackSR(h, i, c) KnapsackSR(h,i,c)
表示在第 h h h个到第 i i i个商品中,容量为 c c c时的最优解
例如,
我们可以发现如下的递推式:
K
n
a
p
s
a
c
k
S
R
(
h
,
i
,
c
)
=
m
a
x
{
K
n
a
p
s
a
c
k
S
R
(
h
,
i
−
1
,
c
−
v
i
)
+
p
i
,
K
n
a
p
s
a
c
k
S
R
(
h
,
i
−
1
,
c
)
}
KnapsackSR(h,i,c)=max\left \{ KnapsackSR(h,i-1,c-v_i)+p_i, KnapsackSR(h,i-1,c) \right \}
KnapsackSR(h,i,c)=max{KnapsackSR(h,i−1,c−vi)+pi,KnapsackSR(h,i−1,c)}
为了方便,将函数修改为
K n a p s a c k S R ( i , c ) KnapsackSR(i, c) KnapsackSR(i,c)
表示在前 i i i个商品中,容量为 c c c时的最优解
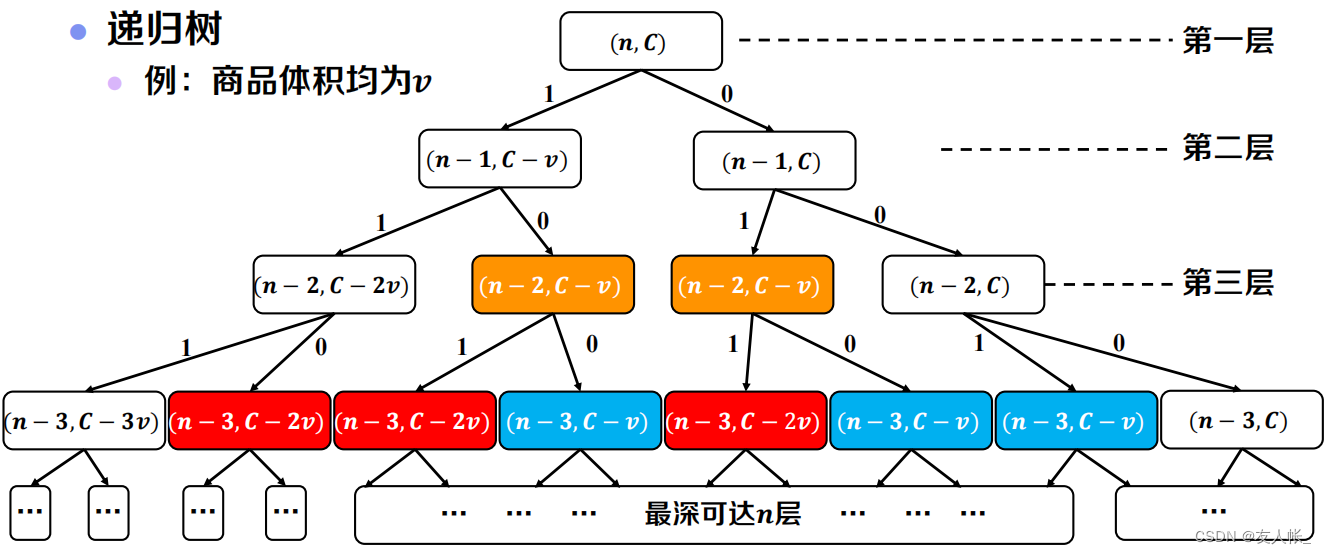
观察其递归树,我们会发现存在大量重叠子问题:
那么如何进一步优化以减少计算量?接下来引入带备忘录的递归。
2.2 带备忘递归
只需构造备忘录 P [ i , c ] P[i,c] P[i,c],表示在前 i i i个商品中选择,背包容量为 c c c时的最优解。
此时的递归树便可以被优化至下图所示:
给出其伪代码:
那么我们是否可以不进行递归,直接求解 P [ i , c ] P[i,c] P[i,c]?答案是肯定的,接下来使用动态规划来解决此问题。
2.3 动态规划
是否还记得我们之前发现的递推式?
K
n
a
p
s
a
c
k
M
R
(
i
,
c
)
=
m
a
x
{
K
n
a
p
s
a
c
k
M
R
(
i
−
1
,
c
−
v
i
)
+
p
i
,
K
n
a
p
s
a
c
k
M
R
(
i
−
1
,
c
)
}
KnapsackMR(i,c)=max\left \{ KnapsackMR(i-1,c-v_i)+p_i, KnapsackMR(i-1,c) \right \}
KnapsackMR(i,c)=max{KnapsackMR(i−1,c−vi)+pi,KnapsackMR(i−1,c)}
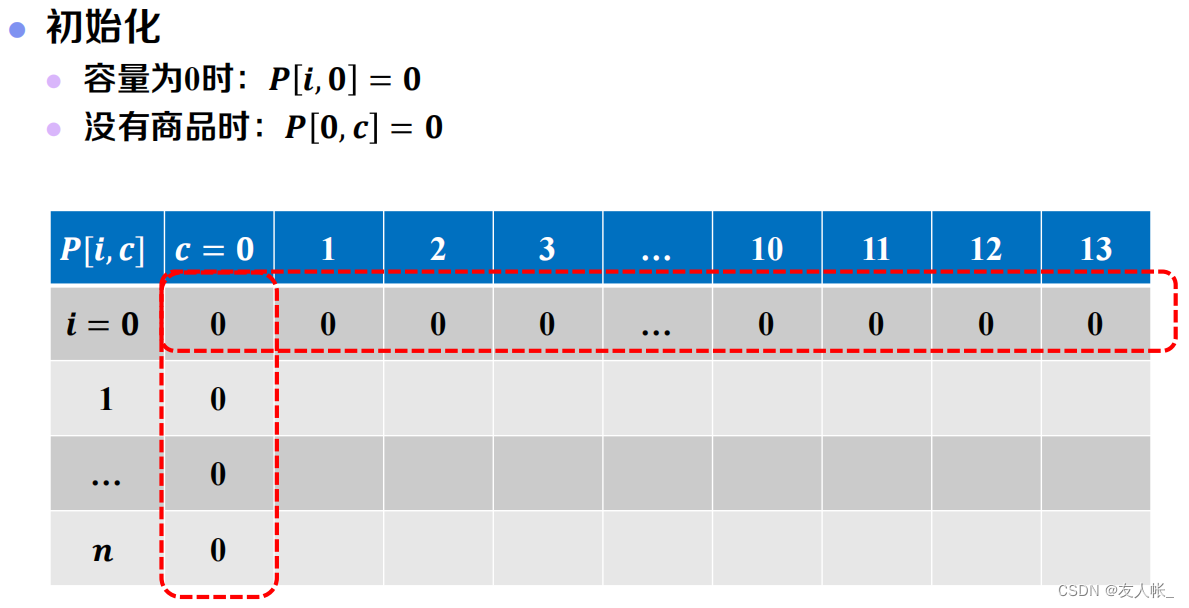
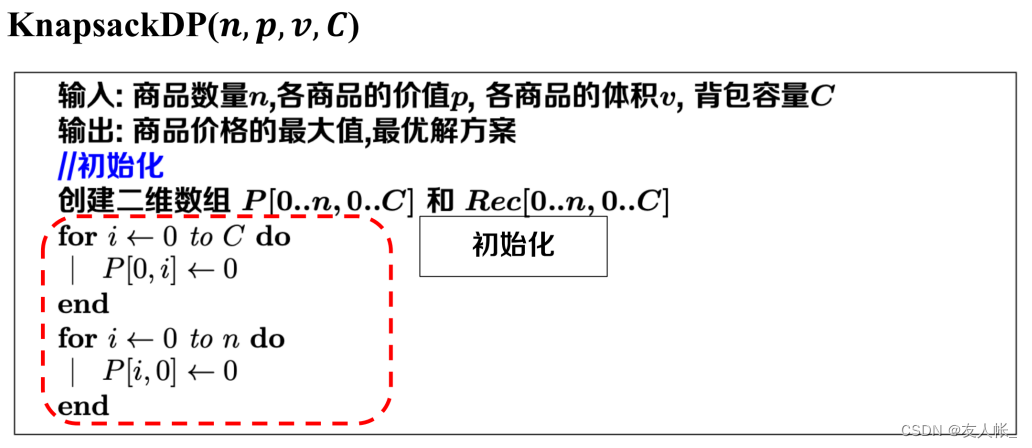
(1)首先,对备忘录进行初始化:
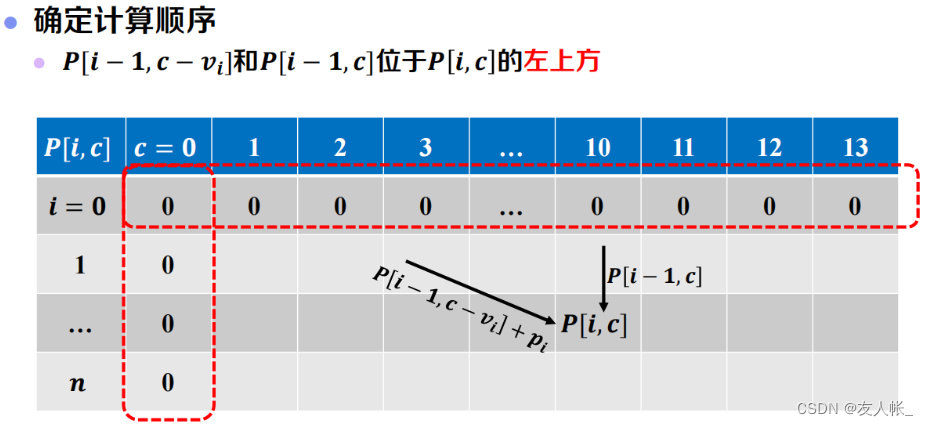
接着,根据递推式,确定计算顺序:
(2)于是,我们根据子问题的依赖关系,确定按照从左到右,从上到下的顺序进行计算。此时最优解出现在备忘录 P P P的右下角。
并且,为了记录选择了哪些商品,我们再引入一个
R
e
c
Rec
Rec数组,用来记录决策过程
R
e
c
[
i
,
c
]
=
{
1
选择第
i
个商品
0
不选第
i
个商品
Rec[i,c]=\left\{\begin{matrix} 1 & 选择第i个商品\\ 0 &不选第i个商品 \end{matrix}\right.
Rec[i,c]={10选择第i个商品不选第i个商品
根据上述关系式,最终可以求解出
P
[
i
]
[
c
]
P[i][c]
P[i][c]和
R
e
c
[
i
]
[
c
]
Rec[i][c]
Rec[i][c]
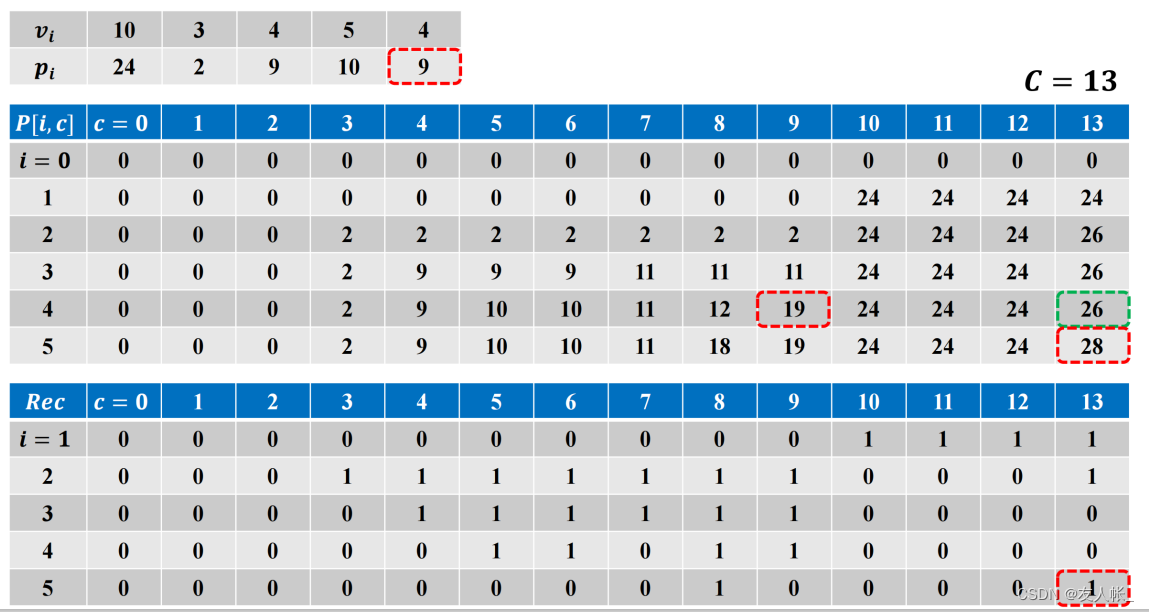
(3)根据 R e c [ i ] [ c ] Rec[i][c] Rec[i][c]数值,逆向搜索追踪最优解。
例如, R e c [ 5 ] [ 13 ] = 1 Rec[5][13]=1 Rec[5][13]=1,那么则选择了商品5,观察 R e c [ 5 − 1 ] [ 13 − v 5 ] = R e c [ 4 ] [ 9 ] = 1 Rec[5-1][13-v_5]=Rec[4][9]=1 Rec[5−1][13−v5]=Rec[4][9]=1,则确定选择了商品4。
如此,最终可以得知选择了商品5,4,3。
其伪代码分为三部分:
①初始化 P [ i ] [ c ] P[i][c] P[i][c]和 R e c [ i ] [ c ] Rec[i][c] Rec[i][c]
②依次计算子问题,记录决策过程
③追踪最优方案
最终可以达到时间复杂度: O ( n C ) O(nC) O(nC),线性时间即可求解。
三、动态规划小结
实际上,带备忘递归和递推求解都叫做动态规划,他们的共同点都是分解问题来寻找关系,但是带备忘递归是自顶向下,而递推求解是自底向上,更加高效。
动态规划一般分为4步:
(1)分析问题结构
给出问题的形式化定义,明确原始问题。
分析问题的最优子结构,只有具有最优子结构性质和重叠子问题的问题才可以使用动态规划来进行求解。
最优子结构性质
①问题的最优解由子问题最优解组合而成
②子问题可以独立求解
(2)建立递推关系
(3)自底向上计算
(4)追踪最优方案